控制系統 - 補償器

---

---

補償器有三種類型：滯後補償器、超前補償器和滯後-超前補償器。這些是最常用的。

滯後補償器

滯後補償器是一種電網路，當施加正弦輸入時，它會產生具有相位滯後的正弦輸出。以下圖顯示了“s”域中的滯後補償器電路。

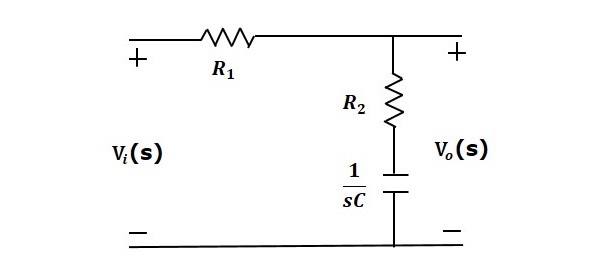
此處，電容與電阻R₂串聯，輸出電壓在此組合上測量。

該滯後補償器的傳遞函式為：

$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$

其中：

$$\tau=R_2C$$

$$\alpha=\frac{R_1+R_2}{R_2}$$

從上式可知，α總是大於1。

從傳遞函式可以看出，滯後補償器在s = − 1/(ατ)處有一個極點，在s = −1/τ處有一個零點。這意味著在滯後補償器的零極點配置中，極點更靠近原點。

將s = jω代入傳遞函式。

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$

相角 φ = arctan(ωτ) − arctan(αωτ)

我們知道，輸出正弦訊號的相位等於輸入正弦訊號和傳遞函式的相位之和。

因此，為了在這個補償器的輸出端產生相位滯後，傳遞函式的相角應該為負。當α > 1時，就會發生這種情況。

超前補償器

超前補償器是一種電網路，當施加正弦輸入時，它會產生具有相位超前的正弦輸出。以下圖顯示了“s”域中的超前補償器電路。

此處，電容與電阻R₁並聯，輸出電壓在電阻R₂上測量。

該超前補償器的傳遞函式為：

$$\frac{V_o(s)}{V_i(s)}=\beta \left( \frac{s\tau+1}{\beta s\tau+1} \right )$$

其中：

$$\tau=R_1C$$

$$\beta=\frac{R_2}{R_1+R_2}$$

從傳遞函式可以看出，超前補償器在s = −1/β處有一個極點，在s = −1/(βτ)處有一個零點。

將s = jω代入傳遞函式。

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\beta \left( \frac{j\omega\tau+1}{\beta j \omega\tau+1} \right )$$

相角 φ = arctan(ωτ) − arctan(βωτ)

我們知道，輸出正弦訊號的相位等於輸入正弦訊號和傳遞函式的相位之和。

因此，為了在這個補償器的輸出端產生相位超前，傳遞函式的相角應該為正。當0 < β < 1時，就會發生這種情況。因此，在超前補償器的零極點配置中，零點更靠近原點。

滯後-超前補償器

滯後-超前補償器是一種電網路，在一個頻率區域產生相位滯後，在另一個頻率區域產生相位超前。它是滯後補償器和超前補償器的組合。以下圖顯示了“s”域中的滯後-超前補償器電路。

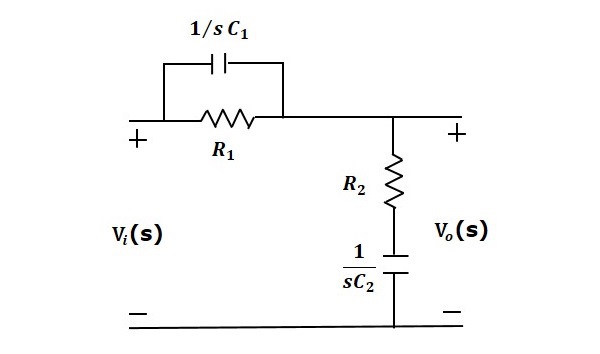
該電路看起來像是兩個補償器級聯連線。因此，該電路的傳遞函式將是超前補償器和滯後補償器傳遞函式的乘積。

$$\frac{V_o(s)}{V_i(s)}=\beta \left( \frac{s\tau_1+1}{\beta s \tau_1+1} \right )\frac{1}{\alpha} \left ( \frac{s+\frac{1}{\tau_2}}{s+\frac{1}{\alpha\tau_2}} \right )$$

我們知道αβ=1。

$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\left ( \frac{s+\frac{1}{\tau_1}}{s+\frac{1}{\beta\tau_1}} \right )\left ( \frac{s+\frac{1}{\tau_2}}{s+\frac{1}{\alpha\tau_2}} \right )$$

其中：

$$\tau_1=R_1C_1$$

$$\tau_2=R_2C_2$$