控制系統 - 伯德圖

---

---

伯德圖或伯德圖由兩張圖組成：

• 幅值圖
• 相點陣圖

在這兩張圖中，x軸表示角頻率（對數刻度）。而y軸在幅值圖中表示開環傳遞函式的幅值（線性刻度），在相點陣圖中表示開環傳遞函式的相位角（線性刻度）。

開環傳遞函式的**幅值**（以dB為單位）為：

$$M=20\: \log|G(j\omega)H(j\omega)|$$

開環傳遞函式的**相位角**（以度為單位）為：

$$\phi=\angle G(j\omega)H(j\omega)$$

**注意** - 對數的底數為10。

伯德圖基礎

下表顯示了開環傳遞函式中各項的斜率、幅值和相位角值。繪製伯德圖時，這些資料非常有用。

考慮開環傳遞函式 $G(s)H(s) = K$。

幅值 $M = 20\: \log K$ dB

相位角 $\phi = 0$ 度

如果 $K = 1$，則幅值為 0 dB。

如果 $K > 1$，則幅值將為正。

如果 $K < 1$，則幅值將為負。

下圖顯示了相應的伯德圖。

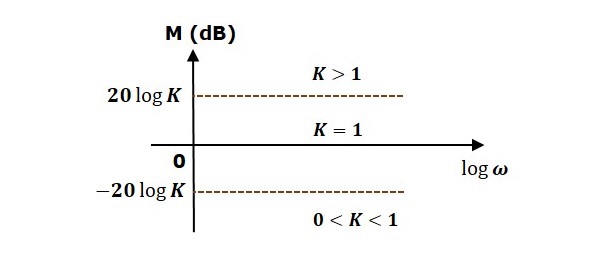
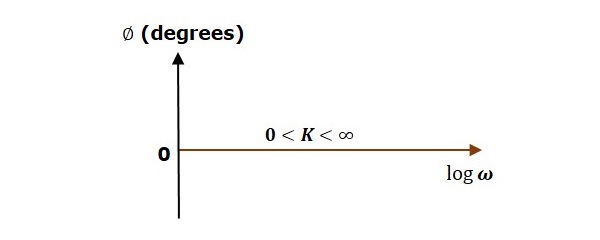
幅值圖是一條水平線，與頻率無關。當 K 值為 1 時，0 dB 線本身就是幅值圖。對於 K 的正值，水平線將向上移動 $20 \:\log K$ dB。對於 K 的負值，水平線將向下移動 $20\: \log K$ dB。對於所有 K 的正值，0 度線本身就是相點陣圖。

考慮開環傳遞函式 $G(s)H(s) = s$。

幅值 $M = 20 \log \omega$ dB

相位角 $\phi = 90^0$

在 $\omega = 0.1$ rad/sec 時，幅值為 -20 dB。

在 $\omega = 1$ rad/sec 時，幅值為 0 dB。

在 $\omega = 10$ rad/sec 時，幅值為 20 dB。

下圖顯示了相應的伯德圖。

幅值圖是一條斜率為 20 dB/dec 的直線。這條線從 $\omega = 0.1$ rad/sec 開始，幅值為 -20 dB，並以相同的斜率繼續。它在 $\omega = 1$ rad/sec 時與 0 dB 線相交。在這種情況下，相點陣圖是 90⁰ 線。

考慮開環傳遞函式 $G(s)H(s) = 1 + s\tau$。

幅值 $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB

相位角 $\phi = \tan^{-1}\omega\tau$ 度

對於 $ω < \frac{1}{\tau}$ ，幅值為 0 dB，相位角為 0 度。

對於 $\omega > \frac{1}{\tau}$ ，幅值為 $20\: \log \omega\tau$ dB，相位角為 90⁰。

下圖顯示了相應的伯德圖。

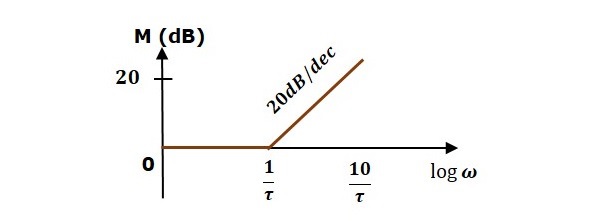
幅值圖在 $\omega=\frac{1}{\tau}$ rad/sec 之前幅值為 0 dB。從 $\omega = \frac{1}{\tau}$ rad/sec 開始，其斜率為 20 dB/dec。在這種情況下，相點陣圖在 $\omega = \frac{1}{\tau}$ rad/sec 之前相位角為 0 度，從這裡開始，相位角為 90⁰。這個伯德圖被稱為**漸近伯德圖**。

由於幅值和相點陣圖是用直線表示的，精確的伯德圖類似於漸近伯德圖。唯一的區別是精確的伯德圖將具有簡單的曲線而不是直線。

同樣，您可以針對表格中給出的開環傳遞函式的其他項繪製伯德圖。