控制系統 - 控制器

---

---

各種型別的控制器用於提高控制系統的效能。在本章中，我們將討論基本的控制器，例如比例控制器、微分控制器和積分控制器。

比例控制器

比例控制器產生一個輸出，該輸出與誤差訊號成正比。

$$u(t) \propto e(t) $$

$$\Rightarrow u(t)=K_P e(t)$$

對兩邊應用拉普拉斯變換 -

$$U(s)=K_P E(s)$$

$$\frac{U(s)}{E(s)}=K_P$$

因此，比例控制器的傳遞函式為 $K_P$。

其中，

U(s) 是執行訊號 u(t) 的拉普拉斯變換

E(s) 是誤差訊號 e(t) 的拉普拉斯變換

K_P 是比例常數

帶有比例控制器的單位負反饋閉環控制系統的方框圖如下所示。

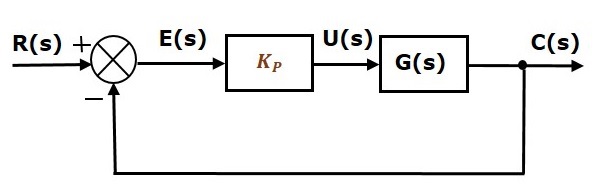
比例控制器用於根據需要更改瞬態響應。

微分控制器

微分控制器產生一個輸出，該輸出是誤差訊號的導數。

$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$$

對兩邊應用拉普拉斯變換。

$$U(s)=K_D sE(s)$$

$$\frac{U(s)}{E(s)}=K_D s$$

因此，微分控制器的傳遞函式為 $K_D s$。

其中，$K_D$ 是微分常數。

帶有微分控制器的單位負反饋閉環控制系統的方框圖如下所示。

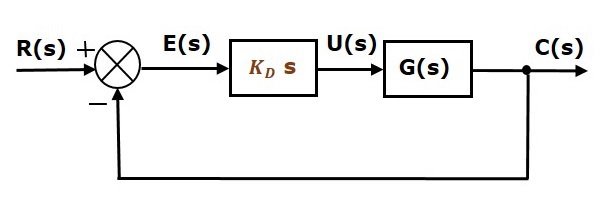
微分控制器用於將不穩定的控制系統轉變為穩定的控制系統。

積分控制器

積分控制器產生一個輸出，該輸出是誤差訊號的積分。

$$u(t)=K_I \int e(t) dt$$

對兩邊應用拉普拉斯變換 -

$$U(s)=\frac{K_I E(s)}{s}$$

$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$

因此，積分控制器的傳遞函式為 $\frac{K_I}{s}$。

其中，$K_I$ 是積分常數。

帶有積分控制器的單位負反饋閉環控制系統的方框圖如下所示。

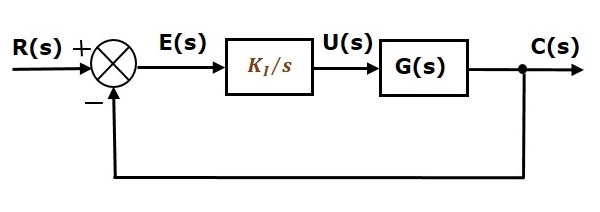
積分控制器用於減小穩態誤差。

現在讓我們討論一下基本控制器的組合。

比例微分 (PD) 控制器

比例微分控制器產生一個輸出，該輸出是比例控制器和微分控制器的輸出的組合。

$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$$

對兩邊應用拉普拉斯變換 -

$$U(s)=(K_P+K_D s)E(s)$$

$$\frac{U(s)}{E(s)}=K_P+K_D s$$

因此，比例微分控制器的傳遞函式為 $K_P + K_D s$。

帶有比例微分控制器的單位負反饋閉環控制系統的方框圖如下所示。

比例微分控制器用於提高控制系統的穩定性，而不影響穩態誤差。

比例積分 (PI) 控制器

比例積分控制器產生一個輸出，該輸出是比例控制器和積分控制器的輸出的組合。

$$u(t)=K_P e(t)+K_I \int e(t) dt$$

對兩邊應用拉普拉斯變換 -

$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$

$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$

因此，比例積分控制器的傳遞函式為 $K_P + \frac{K_I} {s}$。

帶有比例積分控制器的單位負反饋閉環控制系統的方框圖如下所示。

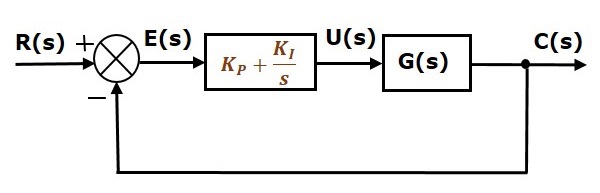
比例積分控制器用於減小穩態誤差，而不影響控制系統的穩定性。

比例積分微分 (PID) 控制器

比例積分微分控制器產生一個輸出，該輸出是比例控制器、積分控制器和微分控制器的輸出的組合。

$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$

對兩邊應用拉普拉斯變換 -

$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$

$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$

因此，比例積分微分控制器的傳遞函式為 $K_P + \frac{K_I} {s} + K_D s$。

帶有比例積分微分控制器的單位負反饋閉環控制系統的方框圖如下所示。

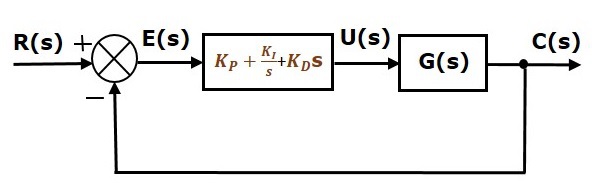
比例積分微分控制器用於提高控制系統的穩定性並減小穩態誤差。