控制系統 - 反饋

---

---

如果輸出或輸出的一部分返回到輸入端並用作系統輸入的一部分，則稱為反饋。反饋在提高控制系統的效能方面發揮著重要作用。在本章中，讓我們討論反饋的型別和反饋的影響。

反饋型別

反饋主要分為兩種型別：

• 正反饋
• 負反饋

正反饋

正反饋將參考輸入 $R(s)$ 和反饋輸出相加。下圖顯示了正反饋控制系統的方框圖。

傳遞函式的概念將在後面的章節中討論。目前，考慮正反饋控制系統的傳遞函式為：

$T=\frac{G}{1-GH}$ (公式 1)

其中，

• T 是正反饋控制系統的傳遞函式或總增益。

• G 是開環增益，它是頻率的函式。

• H 是反饋路徑的增益，它是頻率的函式。

負反饋

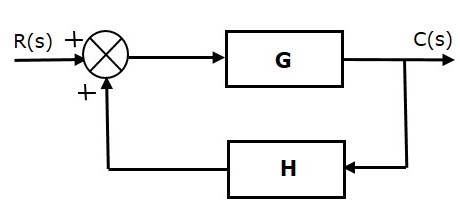
負反饋減少了參考輸入 $R(s)$ 和系統輸出之間的誤差。下圖顯示了負反饋控制系統的方框圖。

負反饋控制系統的傳遞函式為：

$T=\frac{G}{1+GH}$ (公式 2)

其中，

• T 是負反饋控制系統的傳遞函式或總增益。

• G 是開環增益，它是頻率的函式。

• H 是反饋路徑的增益，它是頻率的函式。

上述傳遞函式的推導在後面的章節中給出。

反饋的影響

現在讓我們瞭解反饋的影響。

反饋對總增益的影響

• 從公式 2 可以看出，負反饋閉環控制系統的總增益是 'G' 與 (1+GH) 的比值。因此，總增益可能會增加或減少，具體取決於 (1+GH) 的值。

• 如果 (1+GH) 的值小於 1，則總增益增加。在這種情況下，'GH' 值為負，因為反饋路徑的增益為負。

• 如果 (1+GH) 的值大於 1，則總增益減小。在這種情況下，'GH' 值為正，因為反饋路徑的增益為正。

通常，'G' 和 'H' 都是頻率的函式。因此，反饋將在一個頻率範圍內提高系統的總增益，而在另一個頻率範圍內降低。

反饋對靈敏度的影響

負反饋閉環控制系統（T）的總增益對開環增益（G）變化的靈敏度定義為

$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{T 的百分比變化}{G 的百分比變化}$ (公式 3)

其中，∂T 是由於 G 的增量變化而引起的 T 的增量變化。

我們可以將公式 3 重寫為

$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (公式 4)

對公式 2 的兩邊關於 G 進行偏微分。

$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (公式 5)

從公式 2，我們可以得到

$\frac{G}{T}=1+GH$ (公式 6)

將公式 5 和公式 6 代入公式 4。

$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$

因此，我們得到了閉環控制系統總增益的靈敏度為 (1+GH) 的倒數。因此，靈敏度可能會增加或減少，具體取決於 (1+GH) 的值。

• 如果 (1+GH) 的值小於 1，則靈敏度增加。在這種情況下，'GH' 值為負，因為反饋路徑的增益為負。

• 如果 (1+GH) 的值大於 1，則靈敏度降低。在這種情況下，'GH' 值為正，因為反饋路徑的增益為正。

通常，'G' 和 'H' 都是頻率的函式。因此，反饋將在一個頻率範圍內提高系統增益的靈敏度，而在另一個頻率範圍內降低。因此，我們必須選擇 'GH' 的值，使系統對引數變化不敏感或不太敏感。

反饋對穩定性的影響

• 如果系統的輸出處於控制之下，則稱該系統是穩定的。否則，則稱其為不穩定的。

• 在公式 2 中，如果分母值為零（即 GH = -1），則控制系統的輸出將為無窮大。因此，控制系統變得不穩定。

因此，我們必須正確選擇反饋以使控制系統穩定。

反饋對噪聲的影響

為了瞭解反饋對噪聲的影響，讓我們比較有反饋和無反饋時由於噪聲訊號單獨引起的傳遞函式關係。

考慮一個開環控制系統，其中包含如下所示的噪聲訊號。

由於噪聲訊號單獨引起的開環傳遞函式為

$\frac{C(s)}{N(s)}=G_b$ (公式 7)

它是透過將另一個輸入 $R(s)$ 設定為零而獲得的。

考慮一個閉環控制系統，其中包含如下所示的噪聲訊號。

由於噪聲訊號單獨引起的閉環傳遞函式為

$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (公式 8)

它是透過將另一個輸入 $R(s)$ 設定為零而獲得的。

比較公式 7 和公式 8，

在閉環控制系統中，由於噪聲訊號引起的增益降低了 $(1+G_a G_b H)$ 的因子，前提是 $(1+G_a G_b H)$ 大於 1。