一階系統的響應

---

---

在本節中，我們將討論一階系統的時間響應。考慮以下閉環控制系統的方塊圖。這裡，一個開環傳遞函式 $\frac{1}{sT}$ 連線到一個單位負反饋。

我們知道，具有單位負反饋的閉環控制系統的傳遞函式為：

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

將 $G(s)=\frac{1}{sT}$ 代入上式。

$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$

分母項中 s 的冪為 1。因此，上述傳遞函式是一階的，並且該系統被稱為一階系統。

我們可以將上述方程改寫為

$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$

其中，

• C(s) 是輸出訊號 c(t) 的拉普拉斯變換，

• R(s) 是輸入訊號 r(t) 的拉普拉斯變換，並且

• T 是時間常數。

按照以下步驟獲取一階系統在時域中的響應（輸出）。

• 對輸入訊號 $r(t)$ 進行拉普拉斯變換。

• 考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

• 將 $R(s)$ 的值代入上述方程。

• 如果需要，對 $C(s)$ 進行部分分式展開。

• 對 $C(s)$ 應用拉普拉斯反變換。

在上一節中，我們看到了標準的測試訊號，如脈衝、階躍、斜坡和拋物線。現在讓我們逐一找出每個輸入的一階系統的響應。響應的名稱根據輸入訊號的名稱給出。例如，系統對脈衝輸入的響應稱為脈衝響應。

一階系統的脈衝響應

考慮將單位脈衝訊號作為一階系統的輸入。

所以，$r(t)=\delta (t)$

對等式兩邊進行拉普拉斯變換。

$R(s)=1$

考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

將 $R(s) = 1$ 代入上述方程。

$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$

將上述方程重新排列成拉普拉斯變換的標準形式之一。

$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$

對等式兩邊應用拉普拉斯反變換。

$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$

單位脈衝響應如下圖所示。

單位脈衝響應 c(t) 對於 t 的正值是指數衰減訊號，對於 t 的負值則為零。

一階系統的階躍響應

考慮將單位階躍訊號作為一階系統的輸入。

所以，$r(t)=u(t)$

對等式兩邊進行拉普拉斯變換。

$$R(s)=\frac{1}{s}$$

考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

將 $R(s)=\frac{1}{s}$ 代入上述方程。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$

對 C(s) 進行部分分式展開。

$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$

$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$

在等式兩邊，分母項相同。因此，它們將相互抵消。因此，將分子項相等。

$$1=A\left ( sT+1 \right )+Bs$$

透過將等式兩邊的常數項相等，可以得到 A = 1。

將 A = 1 代入，並將等式兩邊 s 項的係數相等。

$$0=T+B \Rightarrow B=-T$$

將 A = 1 和 B = −T 代入 $C(s)$ 的部分分式展開中。

$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$

對等式兩邊應用拉普拉斯反變換。

$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

單位階躍響應 c(t) 同時具有暫態項和穩態項。

單位階躍響應中的暫態項為：

$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$

單位階躍響應中的穩態項為：

$$c_{ss}(t)=u(t)$$

下圖顯示了單位階躍響應。

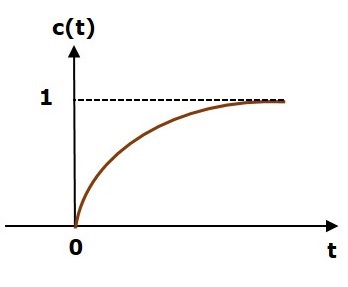
單位階躍響應 c(t) 在 t = 0 和 t 的所有負值時都為零。它從零值逐漸增加，最終在穩態時達到 1。因此，穩態值取決於輸入的幅度。

一階系統的斜坡響應

考慮將單位斜坡訊號作為一階系統的輸入。

$So, r(t)=tu(t)$

對等式兩邊進行拉普拉斯變換。

$$R(s)=\frac{1}{s^2}$$

考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

將 $R(s)=\frac{1}{s^2}$ 代入上述方程。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$

對 $C(s)$ 進行部分分式展開。

$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$

$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$

在等式兩邊，分母項相同。因此，它們將相互抵消。因此，將分子項相等。

$$1=A(sT+1)+Bs(sT+1)+Cs^2$$

透過將等式兩邊的常數項相等，可以得到 A = 1。

將 A = 1 代入，並將等式兩邊 s 項的係數相等。

$$0=T+B \Rightarrow B=-T$$

類似地，將 B = −T 代入，並將等式兩邊 $s^2$ 項的係數相等。您將得到 $C=T^2$。

將 A = 1，B = −T 和 $C = T^2$ 代入 $C(s)$ 的部分分式展開中。

$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$

$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$

對等式兩邊應用拉普拉斯反變換。

$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

單位斜坡響應 c(t) 同時具有暫態項和穩態項。

單位斜坡響應中的暫態項為：

$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$

單位斜坡響應中的穩態項為：

$$c_{ss}(t)=(t-T)u(t)$$

下圖顯示了單位斜坡響應。

單位斜坡響應 c(t) 在 t 的所有正值時都遵循單位斜坡輸入訊號。但是，與輸入訊號存在 T 個單位的偏差。

一階系統的拋物線響應

考慮將單位拋物線訊號作為一階系統的輸入。

所以，$r(t)=\frac{t^2}{2}u(t)$

對等式兩邊進行拉普拉斯變換。

$$R(s)=\frac{1}{s^3}$$

考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$

將 $R(s)=\frac{1}{s^3}$ 代入上述方程。

$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$

對 $C(s)$ 進行部分分式展開。

$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$

簡化後，您將分別得到 A、B、C 和 D 的值為 1、$-T、\: T^2\: 和 \: −T^3$。將這些值代入上述 C(s) 的部分分式展開中。

$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$

對等式兩邊應用拉普拉斯反變換。

$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$

單位拋物線響應 c(t) 同時具有暫態項和穩態項。

單位拋物線響應中的暫態項為

$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$

單位拋物線響應中的穩態項為

$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$

從這些響應中，我們可以得出結論，一階控制系統在斜坡和拋物線輸入下不穩定，因為即使在無限長的時間內，這些響應也會不斷增加。一階控制系統在脈衝和階躍輸入下是穩定的，因為這些響應具有有界輸出。但是，脈衝響應沒有穩態項。因此，階躍訊號在時域中被廣泛用於根據其響應分析控制系統。