
- 控制系統教程
- 控制系統 - 首頁
- 控制系統 - 簡介
- 控制系統 - 反饋
- 數學模型
- 機械系統的建模
- 機械系統的電學類比
- 控制系統 - 方框圖
- 方框圖代數
- 方框圖簡化
- 訊號流圖
- 梅森增益公式
- 時間響應分析
- 一階系統的響應
- 二階系統的響應
- 時域指標
- 穩態誤差
- 控制系統 - 穩定性
- 控制系統 - 穩定性分析
- 控制系統 - 根軌跡
- 根軌跡的繪製
- 頻率響應分析
- 控制系統 - 波特圖
- 波特圖的繪製
- 控制系統 - 極座標圖
- 控制系統 - 奈奎斯特圖
- 控制系統 - 補償器
- 控制系統 - 控制器
- 控制系統 - 狀態空間模型
- 狀態空間分析
- 控制系統有用資源
- 控制系統 - 快速指南
- 控制系統 - 有用資源
- 控制系統 - 討論
機械系統的電學類比
如果滿足以下兩個條件,則稱兩個系統為互為類比。
- 這兩個系統在物理上是不同的
- 這兩個系統的微分方程模型相同
電氣系統和機械系統是兩個物理上不同的系統。平移機械系統的電學類比有兩種型別。分別是力-電壓類比和力-電流類比。
力-電壓類比
在力-電壓類比中,將平移機械系統的數學方程與電氣系統的網孔方程進行比較。
考慮以下所示的平移機械系統。
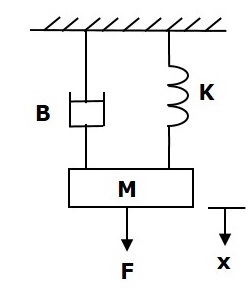
該系統的力平衡方程為
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (公式1)
考慮以下所示的電氣系統。該電路由電阻器、電感器和電容器組成。所有這些元件都串聯連線。施加到該電路的輸入電壓為$V$伏特,流過電路的電流為$i$安培。
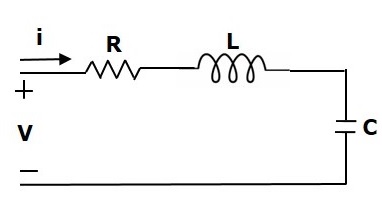
該電路的網孔方程為
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (公式2)
將$i=\frac{\text{d}q}{\text{d}t}$代入公式2。
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (公式3)
透過比較公式1和公式3,我們將得到平移機械系統和電氣系統的類比量。下表顯示了這些類比量。
| 平移機械系統 | 電氣系統 |
|---|---|
| 力(F) | 電壓(V) |
| 質量(M) | 電感(L) |
| 摩擦係數(B) | 電阻(R) |
| 彈簧常數(K) | 電容的倒數 $(\frac{1}{c})$ |
| 位移(x) | 電荷(q) |
| 速度(v) | 電流(i) |
類似地,旋轉機械系統存在轉矩-電壓類比。現在讓我們討論一下這種類比。
轉矩-電壓類比
在這種類比中,將旋轉機械系統的數學方程與電氣系統的網孔方程進行比較。
旋轉機械系統如下圖所示。
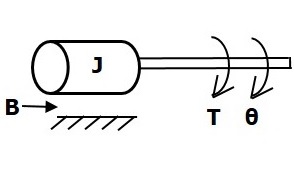
轉矩平衡方程為
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (公式4)
透過比較公式4和公式3,我們將得到旋轉機械系統和電氣系統的類比量。下表顯示了這些類比量。
| 旋轉機械系統 | 電氣系統 |
|---|---|
| 轉矩(T) | 電壓(V) |
| 轉動慣量(J) | 電感(L) |
| 旋轉摩擦係數(B) | 電阻(R) |
| 扭轉彈簧常數(K) | 電容的倒數 $(\frac{1}{c})$ |
| 角位移(θ) | 電荷(q) |
| 角速度(ω) | 電流(i) |
力-電流類比
在力-電流類比中,將平移機械系統的數學方程與電氣系統的節點方程進行比較。
考慮以下所示的電氣系統。該電路由電流源、電阻器、電感器和電容器組成。所有這些元件都並聯連線。
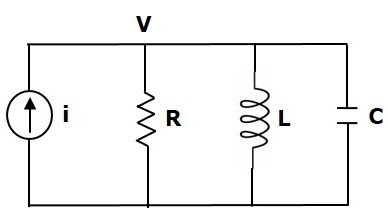
節點方程為
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (公式5)
將$V=\frac{\text{d}\Psi}{\text{d}t}$代入公式5。
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (公式6)
透過比較公式1和公式6,我們將得到平移機械系統和電氣系統的類比量。下表顯示了這些類比量。
| 平移機械系統 | 電氣系統 |
|---|---|
| 力(F) | 電流(i) |
| 質量(M) | 電容(C) |
| 摩擦係數(B) | 電阻的倒數$(\frac{1}{R})$ |
| 彈簧常數(K) | 電感的倒數$(\frac{1}{L})$ |
| 位移(x) | 磁通量(ψ) |
| 速度(v) | 電壓(V) |
類似地,旋轉機械系統存在轉矩-電流類比。現在讓我們討論一下這種類比。
轉矩-電流類比
在這種類比中,將旋轉機械系統的數學方程與電氣系統的節點網孔方程進行比較。
透過比較公式4和公式6,我們將得到旋轉機械系統和電氣系統的類比量。下表顯示了這些類比量。
| 旋轉機械系統 | 電氣系統 |
|---|---|
| 轉矩(T) | 電流(i) |
| 轉動慣量(J) | 電容(C) |
| 旋轉摩擦係數(B) | 電阻的倒數$(\frac{1}{R})$ |
| 扭轉彈簧常數(K) | 電感的倒數$(\frac{1}{L})$ |
| 角位移(θ) | 磁通量(ψ) |
| 角速度(ω) | 電壓(V) |
本章討論了機械系統的電學類比。這些類比有助於從類似的電氣系統研究和分析非電氣系統,例如機械系統。
