控制系統 - 方塊圖化簡

前面章節中討論的概念有助於化簡（簡化）方塊圖。

方塊圖化簡規則

遵循以下規則來簡化（化簡）包含許多方塊、加法點和取樣點的方塊圖。

• 規則 1 - 檢查串聯連線的方塊並進行簡化。

• 規則 2 - 檢查並聯連線的方塊並進行簡化。

• 規則 3 - 檢查反饋迴路中的方塊並進行簡化。

• 規則 4 - 如果在簡化過程中取樣點出現問題，將其向右移動。

• 規則 5 - 如果在簡化過程中加法點出現問題，將其向左移動。

• 規則 6 - 重複上述步驟，直到得到簡化形式，即單個方塊。

注意 - 此單個方塊中存在的傳遞函式是整個方塊圖的傳遞函式。

示例

考慮下圖所示的方塊圖。讓我們使用方塊圖化簡規則來簡化（化簡）此方塊圖。

步驟 1 - 對方塊 $G_1$ 和 $G_2$ 使用規則 1。對方塊 $G_3$ 和 $G_4$ 使用規則 2。修改後的方塊圖如下所示。

步驟 2 - 對方塊 $G_1G_2$ 和 $H_1$ 使用規則 3。對方塊 $G_5$ 後面的取樣點使用規則 4 進行移動。修改後的方塊圖如下所示。

步驟 3 - 對方塊 $(G_3 + G_4)$ 和 $G_5$ 使用規則 1。修改後的方塊圖如下所示。

步驟 4 - 對方塊 $(G_3 + G_4)G_5$ 和 $H_3$ 使用規則 3。修改後的方塊圖如下所示。

步驟 5 - 對串聯連線的方塊使用規則 1。修改後的方塊圖如下所示。

步驟 6 - 對反饋迴路中的方塊使用規則 3。修改後的方塊圖如下所示。這是簡化的方塊圖。

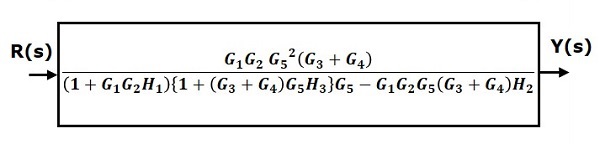
因此，系統的傳遞函式為

$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$

注意 - 為了計算具有多個輸入的方塊圖的傳遞函式，請按順序執行以下步驟。

• 步驟 1 - 透過一次考慮一個輸入並使其餘輸入為零來找到方塊圖的傳遞函式。

• 步驟 2 - 對其餘輸入重複步驟 1。

• 步驟 3 - 透過將所有這些傳遞函式相加來獲得總的傳遞函式。

對於複雜的系統，方塊圖化簡過程需要更多時間。因為，我們必須在每個步驟之後繪製（部分簡化）的方塊圖。因此，為了克服這個缺點，可以使用訊號流圖（表示）。

在接下來的兩章中，我們將討論與訊號流圖相關的概念，即如何從給定的方塊圖中表示訊號流圖，以及僅使用增益公式而不進行任何化簡過程即可計算傳遞函式。