
- 控制系統教程
- 控制系統 - 首頁
- 控制系統 - 簡介
- 控制系統 - 反饋
- 數學模型
- 機械系統的建模
- 機械系統的電氣模擬
- 控制系統 - 方框圖
- 方框圖代數
- 方框圖簡化
- 訊號流圖
- 梅森增益公式
- 時間響應分析
- 一階系統的響應
- 二階系統的響應
- 時域指標
- 穩態誤差
- 控制系統 - 穩定性
- 控制系統 - 穩定性分析
- 控制系統 - 根軌跡
- 根軌跡的繪製
- 頻率響應分析
- 控制系統 - 波德圖
- 波德圖的繪製
- 控制系統 - 極座標圖
- 控制系統 - 奈奎斯特圖
- 控制系統 - 補償器
- 控制系統 - 控制器
- 控制系統 - 狀態空間模型
- 狀態空間分析
- 控制系統有用資源
- 控制系統 - 快速指南
- 控制系統 - 有用資源
- 控制系統 - 討論
控制系統 - 極座標圖
在之前的章節中,我們討論了波德圖。在那裡,我們分別繪製了幅值和相位與頻率的關係曲線。現在讓我們討論極座標圖。極座標圖是在幅值和相位之間繪製的曲線圖。這裡,幅值僅用普通值表示。
G(jω)H(jω)的極座標形式為:
$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$
極座標圖是透過改變ω從零到∞來繪製G(jω)H(jω)的幅值和相位角之間的曲線圖。極座標圖紙如下所示。
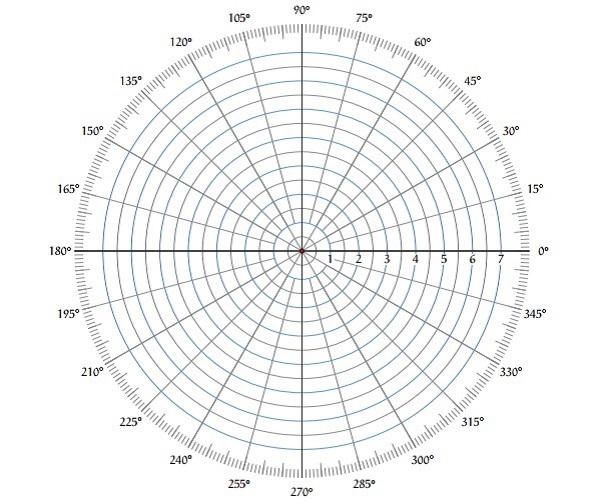
該圖紙由同心圓和徑向線組成。同心圓和徑向線分別表示幅值和相位角。這些角度以逆時針方向用正值表示。類似地,我們可以用順時針方向的負值表示角度。例如,逆時針方向的2700角等於順時針方向的−900角。
繪製極座標圖的規則
請遵循以下規則繪製極座標圖。
在開環傳遞函式中,將s替換為jω。
寫出G(jω)H(jω)的幅值和相位的表示式。
透過將ω=0代入,找到G(jω)H(jω)的起始幅值和相位。因此,極座標圖從此幅值和相位角開始。
透過將ω=∞代入,找到G(jω)H(jω)的結束幅值和相位。因此,極座標圖以此幅值和相位角結束。
檢查極座標圖是否與實軸相交,方法是將G(jω)H(jω)的虛數項設為零,並找到ω的值。
檢查極座標圖是否與虛軸相交,方法是將G(jω)H(jω)的實數項設為零,並找到ω的值。
為了更清晰地繪製極座標圖,請考慮ω的其他值,找到G(jω)H(jω)的幅值和相位。
示例
考慮閉環控制系統的開環傳遞函式。
$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$
讓我們使用上述規則繪製該控制系統的極座標圖。
步驟1 - 在開環傳遞函式中,將s替換為jω。
$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$
開環傳遞函式的幅值為:
$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$
開環傳遞函式的相位角為:
$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$
步驟2 - 下表顯示了開環傳遞函式在ω=0 rad/sec和ω=∞ rad/sec時的幅值和相位角。
| 頻率 (rad/sec) | 幅值 | 相位角 (度) |
|---|---|---|
| 0 | 0 | ∞ |
| 0 | 0 | -90 或 270 |
∞
-270 或 90
因此,極座標圖從(∞,−900)開始,在(0,−2700)結束。括號中的第一項和第二項分別表示幅值和相位角。
步驟3 - 基於起始和結束極座標,該極座標圖將與負實軸相交。與負實軸對應的相位角為−1800或1800。因此,透過將開環傳遞函式的相位角等於−1800或1800,我們將得到ω值為√2。
