控制系統 - 方塊圖

---

---

方塊圖由單個方塊或多個方塊組合而成。它們用於以圖形方式表示控制系統。

方塊圖的基本要素

方塊圖的基本要素包括方塊、加法點和取樣點。讓我們考慮以下圖所示的閉環控制系統的方塊圖來識別這些元素。

上述方塊圖包含兩個具有傳遞函式 G(s) 和 H(s) 的方塊。它還包含一個加法點和一個取樣點。箭頭指示訊號流的方向。現在讓我們逐一討論這些元素。

方塊

元件的傳遞函式由方塊表示。方塊具有單個輸入和單個輸出。

下圖顯示了一個具有輸入 X(s)、輸出 Y(s) 和傳遞函式 G(s) 的方塊。

傳遞函式，$G(s)=\frac{Y(s)}{X(s)}$

$$\Rightarrow Y(s)=G(s)X(s)$$

方塊的輸出是透過將方塊的傳遞函式乘以輸入得到的。

加法點

加法點用一個內部帶有十字 (X) 的圓圈表示。它有兩個或多個輸入和一個輸出。它產生輸入的代數和。它還可以根據輸入的極性執行輸入的求和或減法或求和和減法的組合。讓我們逐一瞭解這三種運算。

下圖顯示了具有兩個輸入 (A、B) 和一個輸出 (Y) 的加法點。這裡，輸入 A 和 B 具有正號。因此，加法點產生輸出 Y 為A 和 B 的和。

即，Y = A + B。

下圖顯示了具有兩個輸入 (A、B) 和一個輸出 (Y) 的加法點。這裡，輸入 A 和 B 具有相反的符號，即 A 具有正號，B 具有負號。因此，加法點產生輸出Y為A 和 B 的差。

Y = A + (-B) = A - B。

下圖顯示了具有三個輸入 (A、B、C) 和一個輸出 (Y) 的加法點。這裡，輸入 A 和 B 具有正號，C 具有負號。因此，加法點產生輸出Y為

Y = A + B + (−C) = A + B − C。

取樣點

取樣點是一個點，從中可以將相同的輸入訊號傳遞到多個分支。這意味著藉助取樣點，我們可以將相同的輸入應用於一個或多個方塊、加法點。

在下圖中，取樣點用於將相同的輸入 R(s) 連線到兩個或多個方塊。

在下圖中，取樣點用於將輸出 C(s) 作為其中一個輸入連線到加法點。

電氣系統的方塊圖表示

在本節中，讓我們用方塊圖表示一個電氣系統。電氣系統主要包含三個基本元件——電阻器、電感器和電容器。

考慮以下圖所示的 RLC 串聯電路。其中，V_i(t) 和 V_o(t) 分別為輸入電壓和輸出電壓。設 i(t) 為流過電路的電流。該電路處於時域。

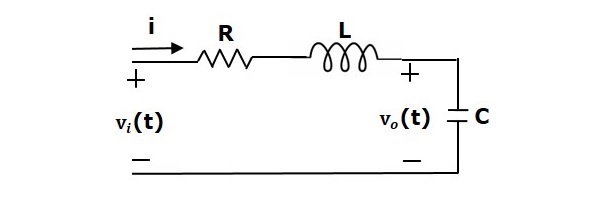
透過對該電路應用拉普拉斯變換，將得到 s 域中的電路。電路如下圖所示。

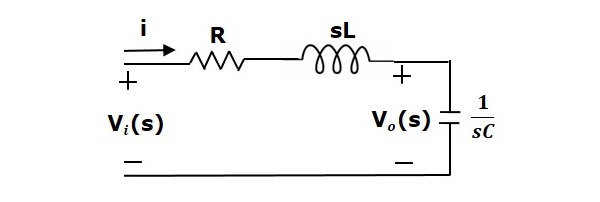
從上述電路，我們可以寫出

$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$

$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (公式 1)

$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (公式 2)

現在讓我們分別繪製這兩個公式的方塊圖。然後將這些方塊圖正確地組合起來，以獲得 RLC 串聯電路（s 域）的整體方塊圖。

公式 1 可以用一個具有傳遞函式 $\frac{1}{R+sL}$ 的方塊來實現。該方塊的輸入和輸出分別是 $\left \{ V_i(s)-V_o(s) \right \}$ 和 $I(s)$。我們需要一個加法點來獲得 $\left \{ V_i(s)-V_o(s) \right \}$。公式 1 的方塊圖如下圖所示。

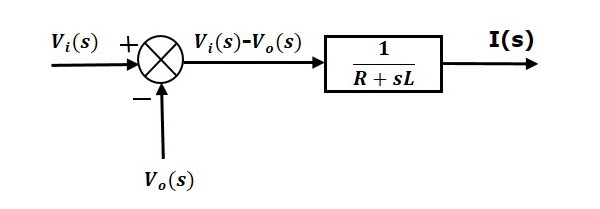
公式 2 可以用一個具有傳遞函式 $\frac{1}{sC}$ 的方塊來實現。該方塊的輸入和輸出分別是 $I(s)$ 和 $V_o(s)$。公式 2 的方塊圖如下圖所示。

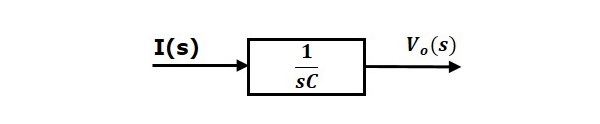
RLC 串聯電路（s 域）的整體方塊圖如下圖所示。

同樣，您只需遵循此簡單過程即可繪製任何電氣電路或系統的方塊圖。

• 透過應用拉普拉斯變換，將時域電氣電路轉換為 s 域電氣電路。

• 寫下流過所有串聯支路元件的電流和跨越所有並聯支路的電壓的方程。

• 分別繪製所有上述方程的方塊圖。

• 將所有這些方塊圖正確地組合起來，以獲得電氣電路（s 域）的整體方塊圖。