- Matlab 教程
- MATLAB - 主頁
- MATLAB - 概述
- MATLAB - 特性
- MATLAB - 環境設定
- MATLAB - 編輯器
- MATLAB - 線上
- MATLAB - 工作區
- MATLAB - 語法
- MATLAB - 變數
- MATLAB - 命令
- MATLAB - 資料型別
- MATLAB - 運算子
- MATLAB - 日期和時間
- MATLAB - 數字
- MATLAB - 隨機數
- MATLAB - 字串和字元
- MATLAB - 文字格式化
- MATLAB - 時間表
- MATLAB - M 檔案
- MATLAB - 冒號表示法
- MATLAB - 資料匯入
- MATLAB - 資料輸出
- MATLAB - 資料歸一化
- MATLAB - 預定義變數
- MATLAB - 決策
- MATLAB - 決策語句
- MATLAB - If End 語句
- MATLAB - If Else 語句
- MATLAB - If…Elseif Else 語句
- MATLAB - 巢狀 If 語句
- MATLAB - Switch 語句
- MATLAB - 巢狀 Switch
- MATLAB - 迴圈
- MATLAB - 迴圈
- MATLAB - For 迴圈
- MATLAB - While 迴圈
- MATLAB - 巢狀迴圈
- MATLAB - Break 語句
- MATLAB - Continue 語句
- MATLAB - End 語句
- MATLAB - 陣列
- MATLAB - 陣列
- MATLAB - 向量
- MATLAB - 轉置運算子
- MATLAB - 陣列索引
- MATLAB - 多維陣列
- MATLAB - 相容陣列
- MATLAB - 分類陣列
- MATLAB - 元胞陣列
- MATLAB - 矩陣
- MATLAB - 稀疏矩陣
- MATLAB - 表格
- MATLAB - 結構體
- MATLAB - 陣列乘法
- MATLAB - 陣列除法
- MATLAB - 陣列函式
- MATLAB - 函式
- MATLAB - 函式
- MATLAB - 函式引數
- MATLAB - 匿名函式
- MATLAB - 巢狀函式
- MATLAB - Return 語句
- MATLAB - 空函式
- MATLAB - 區域性函式
- MATLAB - 全域性變數
- MATLAB - 函式控制代碼
- MATLAB - 濾波器函式
- MATLAB - 階乘
- MATLAB - 私有函式
- MATLAB - 子函式
- MATLAB - 遞迴函式
- MATLAB - 函式優先順序順序
- MATLAB - Map 函式
- MATLAB - Mean 函式
- MATLAB - End 函式
- MATLAB - 錯誤處理
- MATLAB - 錯誤處理
- MATLAB - Try...Catch 語句
- MATLAB - 除錯
- MATLAB - 繪圖
- MATLAB - 繪圖
- MATLAB - 繪製陣列
- MATLAB - 繪製向量
- MATLAB - 條形圖
- MATLAB - 直方圖
- MATLAB - 圖形
- MATLAB - 2D 線性圖
- MATLAB - 3D 圖
- MATLAB - 格式化繪圖
- MATLAB - 對數座標軸圖
- MATLAB - 繪製誤差條
- MATLAB - 繪製 3D 等值線圖
- MATLAB - 極座標圖
- MATLAB - 散點圖
- MATLAB - 繪製表示式或函式
- MATLAB - 繪製矩形
- MATLAB - 繪製頻譜圖
- MATLAB - 繪製網格曲面
- MATLAB - 繪製正弦波
- MATLAB - 插值
- MATLAB - 插值
- MATLAB - 線性插值
- MATLAB - 2D 陣列插值
- MATLAB - 3D 陣列插值
- MATLAB - 多項式
- MATLAB - 多項式
- MATLAB - 多項式加法
- MATLAB - 多項式乘法
- MATLAB - 多項式除法
- MATLAB - 多項式的導數
- MATLAB - 變換
- MATLAB - 變換
- MATLAB - 拉普拉斯變換
- MATLAB - 拉普拉斯濾波器
- MATLAB - 高斯-拉普拉斯濾波器
- MATLAB - 逆傅立葉變換
- MATLAB - 傅立葉變換
- MATLAB - 快速傅立葉變換
- MATLAB - 2D 逆餘弦變換
- MATLAB - 向座標軸新增圖例
- MATLAB - 面向物件
- MATLAB - 面向物件程式設計
- MATLAB - 類和物件
- MATLAB - 函式過載
- MATLAB - 運算子過載
- MATLAB - 使用者定義類
- MATLAB - 複製物件
- MATLAB - 代數
- MATLAB - 線性代數
- MATLAB - 高斯消元法
- MATLAB - 高斯-約旦消元法
- MATLAB - 簡化行階梯形式
- MATLAB - 特徵值和特徵向量
- MATLAB - 積分
- MATLAB - 積分
- MATLAB - 二重積分
- MATLAB - 梯形法則
- MATLAB - 辛普森法則
- MATLAB - 雜項
- MATLAB - 微積分
- MATLAB - 微分
- MATLAB - 矩陣的逆
- MATLAB - GNU Octave
- MATLAB - Simulink
- MATLAB - 有用資源
- MATLAB - 快速指南
- MATLAB - 有用資源
- MATLAB - 討論
MATLAB - 快速指南
MATLAB - 概述
MATLAB(矩陣實驗室)是一種第四代高階程式語言和互動式環境,用於數值計算、視覺化和程式設計。
MATLAB 由 MathWorks 開發。
它允許進行矩陣操作;函式和資料的繪圖;演算法的實現;使用者介面的建立;與用其他語言編寫的程式介面,包括 C、C++、Java 和 FORTRAN;分析資料;開發演算法;以及建立模型和應用程式。
它具有許多內建命令和數學函式,可幫助您進行數學計算、生成繪圖和執行數值方法。
MATLAB 的計算數學能力
MATLAB 用於計算數學的各個方面。以下是它最常用於的一些常用數學計算:
- 處理矩陣和陣列
- 2D 和 3D 繪圖和圖形
- 線性代數
- 代數方程
- 非線性函式
- 統計
- 資料分析
- 微積分和微分方程
- 數值計算
- 積分
- 變換
- 曲線擬合
- 各種其他特殊函式
MATLAB 的特性
以下是 MATLAB 的基本特性:
它是一種用於數值計算、視覺化和應用程式開發的高階語言。
它還提供了一個互動式環境,用於迭代探索、設計和解決問題。
它提供了豐富的數學函式庫,用於線性代數、統計、傅立葉分析、濾波、最佳化、數值積分和求解常微分方程。
它提供了用於視覺化資料和建立自定義繪圖的內建圖形。
MATLAB 的程式設計介面提供了開發工具,用於提高程式碼質量、可維護性和最大化效能。
它提供了用於構建具有自定義圖形介面的應用程式的工具。
它提供了用於將基於 MATLAB 的演算法與外部應用程式和語言(如 C、Java、.NET 和 Microsoft Excel)整合的函式。
MATLAB 的用途
MATLAB 廣泛用作科學和工程中的計算工具,涵蓋物理學、化學、數學和所有工程學科。它用於各種應用,包括:
- 訊號處理和通訊
- 影像和影片處理
- 控制系統
- 測試和測量
- 計算金融
- 計算生物學
MATLAB - 環境設定
本地環境設定
設定 MATLAB 環境只需點選幾下即可。安裝程式可以從這裡下載。
MathWorks 提供許可產品、試用版和學生版。您需要登入網站並等待一段時間以獲得他們的批准。
下載安裝程式後,可以透過點選幾下安裝軟體。


瞭解 MATLAB 環境
MATLAB 開發 IDE 可以從桌面上建立的圖示啟動。MATLAB 中的主要工作視窗稱為桌面。啟動 MATLAB 時,桌面將以其預設佈局顯示:

桌面包含以下面板:
當前資料夾 - 此面板允許您訪問專案資料夾和檔案。
命令視窗 - 這是在命令列輸入命令的主要區域。它由命令提示符(>>)指示。
工作區 - 工作區顯示從檔案建立和/或匯入的所有變數。
命令歷史記錄 - 此面板顯示或返回在命令列輸入的命令。




設定 GNU Octave
如果您想在您的機器(Linux、BSD、OS X 或 Windows)上使用 Octave,請從下載 GNU Octave下載最新版本。您可以檢視給定的機器安裝說明。
MATLAB - 基本語法
MATLAB 環境的行為類似於一個超級複雜的計算器。您可以在 >> 命令提示符下輸入命令。
MATLAB 是一個解釋型環境。換句話說,您發出一個命令,MATLAB 會立即執行它。
實踐操作
輸入一個有效的表示式,例如:
5 + 5
然後按 ENTER
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
ans = 10
讓我們再舉幾個例子:
3 ^ 2 % 3 raised to the power of 2
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
ans = 9
另一個例子:
sin(pi /2) % sine of angle 90o
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
ans = 1
另一個例子:
7/0 % Divide by zero
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
ans = Inf warning: division by zero
另一個例子:
732 * 20.3
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
ans = 1.4860e+04
MATLAB 為某些數學符號提供了一些特殊表示式,例如 pi 代表 π,Inf 代表 ∞,i(和 j)代表 √-1 等。Nan 代表“非數字”。
在 MATLAB 中使用分號 (;)
分號 (;) 表示語句的結束。但是,如果您想抑制和隱藏表示式的 MATLAB 輸出,請在表示式後新增分號。
例如:
x = 3; y = x + 5
當您單擊“執行”按鈕或鍵入 Ctrl+E 時,MATLAB 會立即執行它,並返回以下結果:
y = 8
添加註釋
百分號 (%) 用於指示註釋行。例如:
x = 9 % assign the value 9 to x
您還可以使用塊註釋運算子 % { 和 % } 編寫註釋塊。
MATLAB 編輯器包含工具和上下文選單項,可幫助您新增、刪除或更改註釋的格式。
常用運算子和特殊字元
MATLAB 支援以下常用運算子和特殊字元:
| 運算子 | 用途 |
|---|---|
| + | 加號;加法運算子。 |
| - | 減號;減法運算子。 |
| * | 標量和矩陣乘法運算子。 |
| .* | 陣列乘法運算子。 |
| ^ | 標量和矩陣冪運算子。 |
| .^ | 陣列冪運算子。 |
| \ | 左除運算子。 |
| / | 右除運算子。 |
| .\ | 陣列左除運算子。 |
| ./ | 陣列右除運算子。 |
| : | 冒號;生成等間距的元素並表示整行或整列。 |
| ( ) | 括號;括起函式引數和陣列索引;覆蓋優先順序。 |
| [ ] | 方括號;括起陣列元素。 |
| . | 小數點。 |
| … | 省略號;續行運算子 |
| , | 逗號;分隔語句和行中的元素 |
| ; | 分號;分隔列並抑制顯示。 |
| % | 百分號;指定註釋並指定格式。 |
| _ | 引號和轉置運算子。 |
| ._ | 非共軛轉置運算子。 |
| = | 賦值運算子。 |
特殊變數和常量
MATLAB 支援以下特殊變數和常量:
| 名稱 | 含義 |
|---|---|
| ans | 最近的答案。 |
| eps | 浮點數精度的精度。 |
| i,j | 虛數單位√-1。 |
| Inf | 無窮大。 |
| NaN | 未定義的數值結果(非數字)。 |
| pi | π值。 |
變數命名
變數名由一個字母后跟任意數量的字母、數字或下劃線組成。
MATLAB區分大小寫。
變數名可以是任意長度,但是MATLAB只使用前N個字元,其中N由函式namelengthmax給出。
儲存您的工作
save命令用於將工作區中的所有變數儲存為一個檔案,該檔案具有.mat副檔名,位於當前目錄中。
例如:
save myfile
您可以稍後隨時使用load命令重新載入該檔案。
load myfile
MATLAB - 變數
在MATLAB環境中,每個變數都是一個數組或矩陣。
您可以用簡單的方式分配變數。例如,
x = 3 % defining x and initializing it with a value
MATLAB將執行上述語句並返回以下結果:
x = 3
它建立一個名為x的1×1矩陣,並在其元素中儲存值3。讓我們再看一個例子,
x = sqrt(16) % defining x and initializing it with an expression
MATLAB將執行上述語句並返回以下結果:
x = 4
請注意:
一旦將變數輸入系統,您以後就可以引用它。
變數必須在使用前具有值。
當表示式返回的結果未分配給任何變數時,系統將其分配給名為ans的變數,該變數以後可以使用。
例如:
sqrt(78)
MATLAB將執行上述語句並返回以下結果:
ans = 8.8318
您可以使用此變數ans:
sqrt(78); 9876/ans
MATLAB將執行上述語句並返回以下結果:
ans = 1118.2
讓我們看另一個例子:
x = 7 * 8; y = x * 7.89
MATLAB將執行上述語句並返回以下結果:
y = 441.84
多重賦值
您可以在同一行進行多次賦值。例如,
a = 2; b = 7; c = a * b
MATLAB將執行上述語句並返回以下結果:
c = 14
我忘記了變數!
who命令顯示您使用過的所有變數名。
who
MATLAB將執行上述語句並返回以下結果:
Your variables are: a ans b c
whos命令顯示有關變數的更多資訊:
- 當前記憶體中的變數
- 每個變數的型別
- 分配給每個變數的記憶體
- 它們是否是複數變數
whos
MATLAB將執行上述語句並返回以下結果:
Attr Name Size Bytes Class ==== ==== ==== ==== ===== a 1x1 8 double ans 1x70 757 cell b 1x1 8 double c 1x1 8 double Total is 73 elements using 781 bytes
clear命令從記憶體中刪除所有(或指定的)變數。
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusively
長賦值
長賦值可以使用省略號(...)擴充套件到另一行。例如,
initial_velocity = 0; acceleration = 9.8; time = 20; final_velocity = initial_velocity + acceleration * time
MATLAB將執行上述語句並返回以下結果:
final_velocity = 196
format命令
預設情況下,MATLAB以四位小數顯示數字。這稱為短格式。
但是,如果您需要更高的精度,則需要使用format命令。
format long命令顯示小數點後16位數字。
例如:
format long x = 7 + 10/3 + 5 ^ 1.2
MATLAB將執行上述語句並返回以下結果:
x = 17.2319816406394
另一個例子:
format short x = 7 + 10/3 + 5 ^ 1.2
MATLAB將執行上述語句並返回以下結果:
x = 17.232
format bank命令將數字四捨五入到兩位小數。例如,
format bank daily_wage = 177.45; weekly_wage = daily_wage * 6
MATLAB將執行上述語句並返回以下結果:
weekly_wage = 1064.70
MATLAB使用指數表示法顯示大數字。
format short e命令允許以四位小數加指數的指數形式顯示。例如,
例如:
format short e 4.678 * 4.9
MATLAB將執行上述語句並返回以下結果:
ans = 2.2922e+01
format long e命令允許以四位小數加指數的指數形式顯示。例如,
format long e x = pi
MATLAB將執行上述語句並返回以下結果:
x = 3.141592653589793e+00
format rat命令給出計算結果的最接近的有理表示式。例如,
format rat 4.678 * 4.9
MATLAB將執行上述語句並返回以下結果:
ans = 34177/1491
建立向量
向量是一維數字陣列。MATLAB允許建立兩種型別的向量:
- 行向量
- 列向量
行向量透過將元素集括在方括號中建立,使用空格或逗號分隔元素。
例如:
r = [7 8 9 10 11]
MATLAB將執行上述語句並返回以下結果:
r = 7 8 9 10 11
另一個例子:
r = [7 8 9 10 11]; t = [2, 3, 4, 5, 6]; res = r + t
MATLAB將執行上述語句並返回以下結果:
res =
9 11 13 15 17
列向量透過將元素集括在方括號中建立,使用分號(;)分隔元素。
c = [7; 8; 9; 10; 11]
MATLAB將執行上述語句並返回以下結果:
c =
7
8
9
10
11
建立矩陣
矩陣是二維數字陣列。
在MATLAB中,矩陣是透過將每一行輸入為一系列空格或逗號分隔的元素來建立的,行的末尾用分號分隔。例如,讓我們建立一個3×3矩陣:
m = [1 2 3; 4 5 6; 7 8 9]
MATLAB將執行上述語句並返回以下結果:
m =
1 2 3
4 5 6
7 8 9
MATLAB - 命令
MATLAB是一個用於數值計算和資料視覺化的互動式程式。您可以透過在MATLAB提示符“>>”上鍵入命令在命令視窗中輸入命令。
在本節中,我們將提供常用的一般MATLAB命令列表。
管理會話的命令
MATLAB提供了各種用於管理會話的命令。下表提供了所有此類命令:
| 命令 | 用途 |
|---|---|
| clc | 清除命令視窗。 |
| clear | 從記憶體中刪除變數。 |
| exist | 檢查檔案或變數是否存在。 |
| global | 宣告變數為全域性變數。 |
| help | 搜尋幫助主題。 |
| lookfor | 在幫助條目中搜索關鍵字。 |
| quit | 停止MATLAB。 |
| who | 列出當前變數。 |
| whos | 列出當前變數(長顯示)。 |
與系統一起工作的命令
MATLAB提供了各種用於與系統一起工作的有用命令,例如將當前工作儲存到工作區中作為檔案,以及稍後載入檔案。
它還提供了各種用於其他與系統相關的活動的命令,例如,顯示日期、列出目錄中的檔案、顯示當前目錄等。
下表顯示了一些常用的與系統相關的命令:
| 命令 | 用途 |
|---|---|
| cd | 更改當前目錄。 |
| date | 顯示當前日期。 |
| delete | 刪除檔案。 |
| diary | 開啟/關閉日記檔案記錄。 |
| dir | 列出當前目錄中的所有檔案。 |
| load | 從檔案載入工作區變數。 |
| path | 顯示搜尋路徑。 |
| pwd | 顯示當前目錄。 |
| save | 將工作區變數儲存到檔案中。 |
| type | 顯示檔案的內容。 |
| what | 列出當前目錄中的所有MATLAB檔案。 |
| wklread | 讀取.wk1電子表格檔案。 |
輸入和輸出命令
MATLAB提供以下輸入和輸出相關命令:
| 命令 | 用途 |
|---|---|
| disp | 顯示陣列或字串的內容。 |
| fscanf | 從檔案讀取格式化資料。 |
| format | 控制螢幕顯示格式。 |
| fprintf | 對螢幕或檔案執行格式化寫入。 |
| input | 顯示提示並等待輸入。 |
| ; | 抑制螢幕列印。 |
fscanf和fprintf命令的行為類似於C scanf和printf函式。它們支援以下格式程式碼:
| 格式程式碼 | 用途 |
|---|---|
| %s | 格式化為字串。 |
| %d | 格式化為整數。 |
| %f | 格式化為浮點數。 |
| %e | 以科學計數法格式化為浮點數。 |
| %g | 以最緊湊的形式格式化:%f或%e。 |
| \n | 在輸出字串中插入新行。 |
| \t | 在輸出字串中插入製表符。 |
format函式具有以下用於數字顯示的形式:
| 格式函式 | 顯示最多 |
|---|---|
| format short | 四位小數(預設)。 |
| format long | 16位小數。 |
| format short e | 五位數字加指數。 |
| format long e | 16位數字加指數。 |
| format bank | 兩位小數。 |
| format + | 正數、負數或零。 |
| format rat | 有理逼近。 |
| format compact | 抑制一些換行符。 |
| format loose | 重置為不太緊湊的顯示模式。 |
向量、矩陣和陣列命令
下表顯示了用於處理陣列、矩陣和向量的各種命令:
| 命令 | 用途 |
|---|---|
| cat | 連線陣列。 |
| find | 查詢非零元素的索引。 |
| length | 計算元素數量。 |
| linspace | 建立等間距向量。 |
| logspace | 建立對數間距向量。 |
| max | 返回最大元素。 |
| min | 返回最小元素。 |
| prod | 每列的乘積。 |
| reshape | 更改大小。 |
| size | 計算陣列大小。 |
| sort | 對每列進行排序。 |
| sum | 對每列求和。 |
| eye | 建立單位矩陣。 |
| ones | 建立全1陣列。 |
| zeros | 建立全0陣列。 |
| cross | 計算矩陣叉積。 |
| dot | 計算矩陣點積。 |
| det | 計算陣列的行列式。 |
| inv | 計算矩陣的逆。 |
| pinv | 計算矩陣的偽逆。 |
| rank | 計算矩陣的秩。 |
| rref | 計算簡化行階梯形。 |
| cell | 建立元胞陣列。 |
| celldisp | 顯示元胞陣列。 |
| cellplot | 顯示元胞陣列的圖形表示。 |
| num2cell | 將數值陣列轉換為元胞陣列。 |
| deal | 匹配輸入和輸出列表。 |
| iscell | 識別元胞陣列。 |
繪圖命令
MATLAB提供了許多用於繪製圖形的命令。下表顯示了一些常用的繪圖命令:
| 命令 | 用途 |
|---|---|
| axis | 設定軸限。 |
| fplot | 函式的智慧繪圖。 |
| grid | 顯示網格線。 |
| plot | 生成xy圖。 |
| 列印繪圖或將繪圖儲存到檔案。 | |
| title | 在繪圖頂部放置文字。 |
| xlabel | 向x軸新增文字標籤。 |
| ylabel | 向y軸新增文字標籤。 |
| axes | 建立座標軸物件。 |
| close | 關閉當前繪圖。 |
| close all | 關閉所有繪圖。 |
| figure | 開啟一個新的圖形視窗。 |
| gtext | 透過滑鼠啟用標籤放置。 |
| hold | 凍結當前繪圖。 |
| legend | 透過滑鼠放置圖例。 |
| refresh | 重新繪製當前圖形視窗。 |
| set | 指定物件(如座標軸)的屬性。 |
| subplot | 在子視窗中建立繪圖。 |
| text | 在圖形中放置字串。 |
| bar | 建立條形圖。 |
| loglog | 建立對數-對數圖。 |
| polar | 創建極座標圖。 |
| semilogx | 建立半對數圖。(對數橫座標)。 |
| semilogy | 建立半對數圖。(對數縱座標)。 |
| stairs | 建立階梯圖。 |
| stem | 建立莖狀圖。 |
MATLAB - M 檔案
到目前為止,我們一直使用 MATLAB 環境作為計算器。但是,MATLAB 也是一種強大的程式語言,以及一個互動式計算環境。
在前面的章節中,您已經學習瞭如何從 MATLAB 命令提示符輸入命令。MATLAB 還允許您將一系列命令寫入檔案,並將該檔案作為一個完整的單元執行,就像編寫函式並呼叫它一樣。
M 檔案
MATLAB 允許編寫兩種程式檔案:
指令碼 − 指令碼檔案是具有.m 副檔名的程式檔案。在這些檔案中,您編寫要一起執行的一系列命令。指令碼不接受輸入也不返回任何輸出。它們對工作區中的資料進行操作。
函式 − 函式檔案也是具有.m 副檔名的程式檔案。函式可以接受輸入並返回輸出。內部變數對函式是區域性的。
您可以使用 MATLAB 編輯器或任何其他文字編輯器來建立您的.m檔案。在本節中,我們將討論指令碼檔案。指令碼檔案包含多行連續的 MATLAB 命令和函式呼叫。您可以透過在命令列鍵入其名稱來執行指令碼。
建立和執行指令碼檔案
要建立指令碼檔案,您需要使用文字編輯器。您可以透過兩種方式開啟 MATLAB 編輯器:
- 使用命令提示符
- 使用 IDE
如果您使用的是命令提示符,請在命令提示符中鍵入edit。這將開啟編輯器。您可以直接鍵入edit,然後鍵入檔名(帶有 .m 副檔名)
edit Or edit <filename>
上述命令將在預設的 MATLAB 目錄中建立檔案。如果您想將所有程式檔案儲存在特定資料夾中,則必須提供完整路徑。
讓我們建立一個名為 progs 的資料夾。在命令提示符 (>>) 處鍵入以下命令:
mkdir progs % create directory progs under default directory chdir progs % changing the current directory to progs edit prog1.m % creating an m file named prog1.m
如果您是第一次建立檔案,MATLAB 會提示您確認。單擊“是”。

或者,如果您使用的是 IDE,請選擇“新建” -> “指令碼”。這也會開啟編輯器並建立一個名為 Untitled 的檔案。您可以在鍵入程式碼後命名並儲存檔案。
在編輯器中鍵入以下程式碼:
NoOfStudents = 6000; TeachingStaff = 150; NonTeachingStaff = 20; Total = NoOfStudents + TeachingStaff ... + NonTeachingStaff; disp(Total);
建立並儲存檔案後,您可以透過兩種方式執行它:
單擊編輯器視窗上的執行按鈕或
只需在命令提示符中鍵入檔名(不帶副檔名):>> prog1
命令視窗提示符顯示結果:
6170
示例
建立一個指令碼檔案,並鍵入以下程式碼:
a = 5; b = 7; c = a + b d = c + sin(b) e = 5 * d f = exp(-d)
編譯並執行上述程式碼後,會產生以下結果:
c = 12 d = 12.657 e = 63.285 f = 3.1852e-06
MATLAB - 資料型別
MATLAB 不需要任何型別宣告或維度語句。每當 MATLAB 遇到一個新的變數名時,它都會建立該變數並分配適當的記憶體空間。
如果變數已存在,則 MATLAB 會用新內容替換原始內容,並在必要時分配新的儲存空間。
例如:
Total = 42
上述語句建立一個名為“Total”的 1×1 矩陣,並在其中儲存值 42。
MATLAB 中可用的資料型別
MATLAB 提供 15 種基本資料型別。每種資料型別儲存的資料都以矩陣或陣列的形式存在。此矩陣或陣列的大小至少為 0×0,並且可以增長到任何大小的矩陣或陣列。
下表顯示了 MATLAB 中最常用的資料型別:
| 序號 | 資料型別和描述 |
|---|---|
| 1 | int8 8 位有符號整數 |
| 2 | uint8 8 位無符號整數 |
| 3 | int16 16 位有符號整數 |
| 4 | uint16 16 位無符號整數 |
| 5 | int32 32 位有符號整數 |
| 6 | uint32 32 位無符號整數 |
| 7 | int64 64 位有符號整數 |
| 8 | uint64 64 位無符號整數 |
| 9 | single 單精度數值資料 |
| 10 | double 雙精度數值資料 |
| 11 | logical 邏輯值 1 或 0,分別表示真和假 |
| 12 | char 字元資料(字串儲存為字元向量) |
| 13 | cell array 索引單元格的陣列,每個單元格都能夠儲存不同維度和資料型別的陣列 |
| 14 | structure 類似 C 的結構體,每個結構體都有命名欄位,能夠儲存不同維度和資料型別的陣列 |
| 15 | function handle 指向函式的指標 |
| 16 | user classes 從使用者定義的類構造的物件 |
| 17 | java classes 從 Java 類構造的物件 |
示例
建立一個包含以下程式碼的指令碼檔案:
str = 'Hello World!' n = 2345 d = double(n) un = uint32(789.50) rn = 5678.92347 c = int32(rn)
編譯並執行上述程式碼後,會產生以下結果:
str = Hello World! n = 2345 d = 2345 un = 790 rn = 5678.9 c = 5679
資料型別轉換
MATLAB 提供各種函式用於將值從一種資料型別轉換為另一種資料型別。下表顯示了資料型別轉換函式:
| 函式 | 用途 |
|---|---|
| char | 轉換為字元陣列(字串) |
| int2str | 將整數資料轉換為字串 |
| mat2str | 將矩陣轉換為字串 |
| num2str | 將數字轉換為字串 |
| str2double | 將字串轉換為雙精度值 |
| str2num | 將字串轉換為數字 |
| native2unicode | 將數字位元組轉換為 Unicode 字元 |
| unicode2native | 將 Unicode 字元轉換為數字位元組 |
| base2dec | 將 N 進位制數字字串轉換為十進位制數字 |
| bin2dec | 將二進位制數字字串轉換為十進位制數字 |
| dec2base | 將十進位制轉換為字串表示的 N 進位制數字 |
| dec2bin | 將十進位制轉換為字串表示的二進位制數字 |
| dec2hex | 將十進位制轉換為字串表示的十六進位制數字 |
| hex2dec | 將十六進位制數字字串轉換為十進位制數字 |
| hex2num | 將十六進位制數字字串轉換為雙精度數字 |
| num2hex | 將單精度和雙精度轉換為 IEEE 十六進位制字串 |
| cell2mat | 將元胞陣列轉換為數值陣列 |
| cell2struct | 將元胞陣列轉換為結構體陣列 |
| cellstr | 從字元陣列建立字串的元胞陣列 |
| mat2cell | 將陣列轉換為元胞陣列,其中元胞的大小可能不同 |
| num2cell | 將陣列轉換為元胞陣列,其中元胞的大小一致 |
| struct2cell | 將結構體轉換為元胞陣列 |
資料型別的確定
MATLAB 提供各種函式用於識別變數的資料型別。
下表提供了用於確定變數資料型別的函式:
| 函式 | 用途 |
|---|---|
| is | 檢測狀態 |
| isa | 確定輸入是否為指定類的物件 |
| iscell | 確定輸入是否為元胞陣列 |
| iscellstr | 確定輸入是否為字串的元胞陣列 |
| ischar | 確定專案是否為字元陣列 |
| isfield | 確定輸入是否為結構體陣列欄位 |
| isfloat | 確定輸入是否為浮點陣列 |
| ishghandle | 對於控制代碼圖形物件控制代碼為真 |
| isinteger | 確定輸入是否為整數陣列 |
| isjava | 確定輸入是否為 Java 物件 |
| islogical | 確定輸入是否為邏輯陣列 |
| isnumeric | 確定輸入是否為數值陣列 |
| isobject | 確定輸入是否為 MATLAB 物件 |
| isreal | 檢查輸入是否為實數陣列 |
| isscalar | 確定輸入是否為標量 |
| isstr | 確定輸入是否為字元陣列 |
| isstruct | 確定輸入是否為結構體陣列 |
| isvector | 確定輸入是否為向量 |
| class | 確定物件的類 |
| validateattributes | 檢查陣列的有效性 |
| whos | 列出工作區中的變數,包括大小和型別 |
示例
建立一個包含以下程式碼的指令碼檔案:
x = 3 isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x) x = 23.54 isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x) x = [1 2 3] isinteger(x) isfloat(x) isvector(x) isscalar(x) x = 'Hello' isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x)
執行該檔案時,會產生以下結果:
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0
MATLAB - 運算子
運算子是告訴編譯器執行特定數學或邏輯操作的符號。MATLAB 旨在主要對整個矩陣和陣列進行操作。因此,MATLAB 中的運算子既作用於標量資料也作用於非標量資料。MATLAB 允許以下型別的基本運算:
- 算術運算子
- 關係運算符
- 邏輯運算子
- 按位運算
- 集合運算
算術運算子
MATLAB 允許兩種不同型別的算術運算:
- 矩陣算術運算
- 陣列算術運算
矩陣算術運算與線性代數中定義的相同。陣列運算對一維和多維陣列都進行逐元素執行。
矩陣運算子和陣列運算子透過句點 (.) 符號區分。但是,由於加法和減法運算對於矩陣和陣列來說是相同的,因此這兩種情況下的運算子相同。下表簡要描述了這些運算子:
| 序號 | 運算子和描述 |
|---|---|
| 1 | + 加法或一元加法。A+B 將儲存在變數 A 和 B 中的值相加。A 和 B 必須具有相同的大小,除非其中一個是標量。標量可以加到任何大小的矩陣上。 |
| 2 | - 減法或一元減法。A-B 從 A 中減去 B 的值。A 和 B 必須具有相同的大小,除非其中一個是標量。標量可以從任何大小的矩陣中減去。 |
| 3 | * 矩陣乘法。C = A*B 是矩陣 A 和 B 的線性代數乘積。更準確地說,
對於非標量 A 和 B,A 的列數必須等於 B 的行數。標量可以乘以任何大小的矩陣。 |
| 4 | .* 陣列乘法。A.*B 是陣列 A 和 B 的逐元素乘積。A 和 B 必須具有相同的大小,除非其中一個是標量。 |
| 5 | / 斜槓或矩陣右除。B/A 粗略地等同於 B*inv(A)。更準確地說,B/A = (A'\B')'。 |
| 6 | ./ 陣列右除。A./B 是元素為 A(i,j)/B(i,j) 的矩陣。A 和 B 必須具有相同的大小,除非其中一個是標量。 |
| 7 | \ 反斜槓或矩陣左除。如果 A 是一個方陣,則 A\B 基本上等同於 inv(A)*B,但計算方式不同。如果 A 是一個 n×n 矩陣,而 B 是一個具有 n 個分量的列向量,或者是一個具有多個此類列的矩陣,則 X = A\B 是方程 AX = B 的解。如果 A 縮放比例不好或接近奇異,則會顯示警告訊息。 |
| 8 | .\ 陣列左除。A.\B 是一個矩陣,其元素為 B(i,j)/A(i,j)。A 和 B 必須具有相同的大小,除非其中一個是標量。 |
| 9 | ^ 矩陣冪。如果 p 是標量,則 X^p 是 X 的 p 次冪。如果 p 是整數,則冪透過重複平方計算。如果整數為負數,則先對 X 求逆。對於 p 的其他值,計算涉及特徵值和特徵向量,例如,如果 [V,D] = eig(X),則 X^p = V*D.^p/V。 |
| 10 | .^ 陣列冪。A.^B 是一個矩陣,其元素為 A(i,j) 的 B(i,j) 次冪。A 和 B 必須具有相同的大小,除非其中一個是標量。 |
| 11 | ' 矩陣轉置。A' 是 A 的線性代數轉置。對於複數矩陣,這是共軛轉置。 |
| 12 | .' 陣列轉置。A.' 是 A 的陣列轉置。對於複數矩陣,這不會涉及共軛。 |
關係運算符
關係運算符也可以作用於標量和非標量資料。陣列的關係運算符對兩個陣列執行逐元素比較,並返回大小相同的邏輯陣列,其中關係為真的元素設定為邏輯 1(真),關係為假的元素設定為邏輯 0(假)。
下表顯示了 MATLAB 中可用的關係運算符 -
| 序號 | 運算子和描述 |
|---|---|
| 1 | < 小於 |
| 2 | <= 小於或等於 |
| 3 | > 大於 |
| 4 | >= 大於或等於 |
| 5 | == 等於 |
| 6 | ~= 不等於 |
邏輯運算子
MATLAB 提供兩種型別的邏輯運算子和函式 -
逐元素 - 這些運算子作用於邏輯陣列的對應元素。
短路 - 這些運算子作用於標量和邏輯表示式。
逐元素邏輯運算子對邏輯陣列逐元素進行運算。符號 &、| 和 ~ 分別是邏輯陣列運算子 AND、OR 和 NOT。
短路邏輯運算子允許對邏輯運算進行短路。符號 && 和 || 分別是邏輯短路運算子 AND 和 OR。
按位運算
按位運算子作用於位並執行逐位運算。&、| 和 ^ 的真值表如下 -
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
假設 A = 60;B = 13;現在以二進位制格式,它們將如下所示 -
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011
MATLAB 提供了各種用於按位運算的函式,如“按位與”、“按位或”和“按位非”運算、移位運算等。
下表顯示了常用的按位運算 -
| 函式 | 用途 |
|---|---|
| bitand(a, b) | 整數 a 和 b 的按位與 |
| bitcmp(a) | a 的按位補碼 |
| bitget(a,pos) | 獲取整數陣列 a 中指定位置 pos 的位 |
| bitor(a, b) | 整數 a 和 b 的按位或 |
| bitset(a, pos) | 設定 a 的特定位置 pos 的位 |
| bitshift(a, k) | 返回 a 左移 k 位的結果,等效於乘以 2k。k 的負值對應於右移位或除以 2|k| 並向負無窮大舍入。任何溢位位都被截斷。 |
| bitxor(a, b) | 整數 a 和 b 的按位異或 |
| swapbytes | 交換位元組順序 |
集合運算
MATLAB 提供了各種用於集合運算的函式,如並集、交集和測試集合成員資格等。
下表顯示了一些常用的集合運算 -
| 序號 | 函式 & 描述 |
|---|---|
| 1 | intersect(A,B) 兩個陣列的集合交集;返回 A 和 B 共有的值。返回的值按排序順序排列。 |
| 2 | intersect(A,B,'rows') 將 A 的每一行和 B 的每一行都視為單個實體,並返回 A 和 B 共有的行。返回矩陣的行按排序順序排列。 |
| 3 | ismember(A,B) 返回一個與 A 大小相同的陣列,其中 A 的元素在 B 中找到的位置為 1(真)。在其他位置,它返回 0(假)。 |
| 4 | ismember(A,B,'rows') 將 A 的每一行和 B 的每一行都視為單個實體,並返回一個向量,其中矩陣 A 的行也是 B 的行的位置為 1(真)。在其他位置,它返回 0(假)。 |
| 5 | issorted(A) 如果 A 的元素按排序順序排列,則返回邏輯 1(真),否則返回邏輯 0(假)。輸入 A 可以是向量或 N×1 或 1×N 字串元胞陣列。如果 A 和 sort(A) 的輸出相等,則認為 A 已排序。 |
| 6 | issorted(A, 'rows') 如果二維矩陣 A 的行按排序順序排列,則返回邏輯 1(真),否則返回邏輯 0(假)。如果 A 和 sortrows(A) 的輸出相等,則認為矩陣 A 已排序。 |
| 7 | setdiff(A,B) 兩個陣列的集合差;返回 A 中不在 B 中的值。返回陣列中的值按排序順序排列。 |
| 8 | setdiff(A,B,'rows') 將 A 的每一行和 B 的每一行都視為單個實體,並返回 A 中不在 B 中的行。返回矩陣的行按排序順序排列。 'rows' 選項不支援元胞陣列。 |
| 9 | setxor 兩個陣列的集合異或 |
| 10 | union 兩個陣列的集合並集 |
| 11 | unique 陣列中的唯一值 |
MATLAB - 決策
決策結構要求程式設計師指定一個或多個條件,由程式進行評估或測試,以及在確定條件為真時要執行的語句或語句,以及可選地在確定條件為假時要執行的其他語句。
以下是大多數程式語言中典型的決策結構的一般形式 -
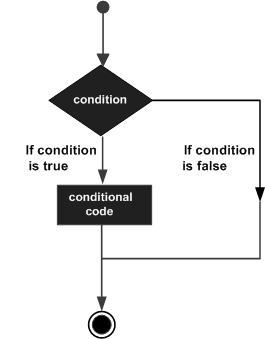
MATLAB 提供以下型別的決策語句。單擊以下連結以檢視其詳細資訊 -
| 序號 | 語句 & 描述 |
|---|---|
| 1 | if ... end 語句
if ... end 語句由一個布林表示式後跟一個或多個語句組成。 |
| 2 | if...else...end 語句
if 語句後面可以跟一個可選的 else 語句,當布林表示式為假時執行。 |
| 3 | If... elseif...elseif...else...end 語句
if 語句後面可以跟一個(或多個)可選的 elseif... 和一個 else 語句,這對於測試各種條件非常有用。 |
| 4 | 巢狀 if 語句
您可以在另一個 if 或 elseif 語句(s)中使用一個 if 或 elseif 語句。 |
| 5 | switch 語句
switch 語句允許將變數與其值列表進行相等性測試。 |
| 6 | 巢狀 switch 語句
您可以在另一個 switch 語句(s)中使用一個 switch 語句。 |
MATLAB - 迴圈型別
可能存在需要執行程式碼塊多次的情況。通常,語句按順序執行。函式中的第一個語句首先執行,然後是第二個語句,依此類推。
程式語言提供各種控制結構,允許更復雜的執行路徑。
迴圈語句允許我們多次執行語句或語句組,以下是大多數程式語言中迴圈語句的一般形式 -

MATLAB 提供以下型別的迴圈來處理迴圈需求。單擊以下連結以檢視其詳細資訊 -
| 序號 | 迴圈型別 & 描述 |
|---|---|
| 1 | while 迴圈
在給定條件為真的情況下重複執行語句或語句組。它在執行迴圈體之前測試條件。 |
| 2 | for 迴圈
多次執行一系列語句,並縮寫管理迴圈變數的程式碼。 |
| 3 | 巢狀迴圈
您可以在任何其他迴圈中使用一個或多個迴圈。 |
迴圈控制語句
迴圈控制語句將其執行從正常順序更改。當執行離開作用域時,在該作用域中建立的所有自動物件都會被銷燬。
MATLAB 支援以下控制語句。單擊以下連結以檢視其詳細資訊。
| 序號 | 控制語句 & 描述 |
|---|---|
| 1 | break 語句
終止 迴圈語句並將執行轉移到迴圈後緊跟的語句。 |
| 2 | continue 語句
導致迴圈跳過其主體剩餘部分,並在重新迭代之前立即重新測試其條件。 |
MATLAB - 向量
向量是一維數字陣列。MATLAB允許建立兩種型別的向量:
- 行向量
- 列向量
行向量
行向量透過將元素集括在方括號中建立,使用空格或逗號分隔元素。
r = [7 8 9 10 11]
MATLAB將執行上述語句並返回以下結果:
r = 7 8 9 10 11
列向量
列向量是透過將元素集括在方括號中建立的,使用分號分隔元素。
c = [7; 8; 9; 10; 11]
MATLAB將執行上述語句並返回以下結果:
c =
7
8
9
10
11
引用向量的元素
您可以透過多種方式引用向量的一個或多個元素。向量 v 的第 i 個分量稱為 v(i)。例如 -
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements v(3)
MATLAB將執行上述語句並返回以下結果:
ans = 3
當您使用冒號引用向量時,例如 v(:),將列出向量的所有分量。
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements v(:)
MATLAB將執行上述語句並返回以下結果:
ans =
1
2
3
4
5
6
MATLAB 允許您從向量中選擇一系列元素。
例如,讓我們建立一個具有 9 個元素的行向量 rv,然後我們將透過編寫 rv(3:7) 引用元素 3 到 7 並建立一個名為 sub_rv 的新向量。
rv = [1 2 3 4 5 6 7 8 9]; sub_rv = rv(3:7)
MATLAB將執行上述語句並返回以下結果:
sub_rv = 3 4 5 6 7
向量運算
在本節中,讓我們討論以下向量運算 -
MATLAB - 矩陣
矩陣是二維數字陣列。
在 MATLAB 中,您可以透過輸入每一行中以逗號或空格分隔的數字作為元素,並使用分號標記每一行的結束來建立矩陣。
例如,讓我們建立一個 4×5 矩陣 a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
MATLAB將執行上述語句並返回以下結果:
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
引用矩陣的元素
要引用矩陣mx中第m行和第n列的元素,我們寫成−
mx(m, n);
例如,要引用上一節中建立的矩陣a的第2行第5列的元素,我們鍵入−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(2,5)
MATLAB將執行上述語句並返回以下結果:
ans = 6
要引用第m列中的所有元素,我們鍵入A(:,m)。
讓我們從矩陣a的第4行的元素建立一個列向量v−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; v = a(:,4)
MATLAB將執行上述語句並返回以下結果:
v =
4
5
6
7
您還可以選擇第m列到第n列的元素,為此我們寫成−
a(:,m:n)
讓我們建立一個較小的矩陣,取第二列和第三列的元素−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
MATLAB將執行上述語句並返回以下結果:
ans =
2 3
3 4
4 5
5 6
同樣,您可以建立一個子矩陣,取矩陣的一部分。
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
MATLAB將執行上述語句並返回以下結果:
ans =
2 3
3 4
4 5
5 6
同樣,您可以建立一個子矩陣,取矩陣的一部分。
例如,讓我們建立一個子矩陣sa,取a的內部子部分−
3 4 5 4 5 6
為此,請寫−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; sa = a(2:3,2:4)
MATLAB將執行上述語句並返回以下結果:
sa =
3 4 5
4 5 6
刪除矩陣中的行或列
您可以透過將空方括號集[]分配給該行或列來刪除矩陣的整行或整列。基本上,[]表示空陣列。
例如,讓我們刪除a的第四行−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a( 4 , : ) = []
MATLAB將執行上述語句並返回以下結果:
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
接下來,讓我們刪除a的第五列−
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(: , 5)=[]
MATLAB將執行上述語句並返回以下結果:
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
示例
在這個例子中,讓我們建立一個3x3的矩陣m,然後我們將這個矩陣的第二行和第三行復制兩次,建立一個4x3的矩陣。
建立一個包含以下程式碼的指令碼檔案:
a = [ 1 2 3 ; 4 5 6; 7 8 9]; new_mat = a([2,3,2,3],:)
執行檔案時,它會顯示以下結果−
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9
矩陣運算
在本節中,讓我們討論以下基本且常用的矩陣運算−
MATLAB - 陣列
MATLAB 中所有資料型別的變數都是多維陣列。向量是一維陣列,矩陣是二維陣列。
我們已經討論了向量和矩陣。在本章中,我們將討論多維陣列。但是,在此之前,讓我們討論一些特殊型別的陣列。
MATLAB中的特殊陣列
在本節中,我們將討論一些建立一些特殊陣列的函式。對於所有這些函式,單個引數建立一個正方形陣列,雙引數建立一個矩形陣列。
zeros()函式建立一個全為零的陣列−
例如:
zeros(5)
MATLAB將執行上述語句並返回以下結果:
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
ones()函式建立一個全為一的陣列−
例如:
ones(4,3)
MATLAB將執行上述語句並返回以下結果:
ans =
1 1 1
1 1 1
1 1 1
1 1 1
eye()函式建立一個單位矩陣。
例如:
eye(4)
MATLAB將執行上述語句並返回以下結果:
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
rand()函式建立一個(0,1)上均勻分佈的隨機數陣列−
例如:
rand(3, 5)
MATLAB將執行上述語句並返回以下結果:
ans = 0.8147 0.9134 0.2785 0.9649 0.9572 0.9058 0.6324 0.5469 0.1576 0.4854 0.1270 0.0975 0.9575 0.9706 0.8003
幻方
幻方是一個正方形,當其元素按行、按列或對角線相加時,會產生相同的和。
magic()函式建立一個幻方陣列。它接受一個單一引數,該引數給出正方形的大小。引數必須是大於或等於3的標量。
magic(4)
MATLAB將執行上述語句並返回以下結果:
ans = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1
多維陣列
在MATLAB中,具有兩個以上維度的陣列稱為多維陣列。MATLAB中的多維陣列是普通二維矩陣的擴充套件。
通常,要生成多維陣列,我們首先建立一個二維陣列並對其進行擴充套件。
例如,讓我們建立一個二維陣列a。
a = [7 9 5; 6 1 9; 4 3 2]
MATLAB將執行上述語句並返回以下結果:
a = 7 9 5 6 1 9 4 3 2
陣列a是一個3x3的陣列;我們可以透過提供如下值來向a新增第三個維度−
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]
MATLAB將執行上述語句並返回以下結果:
a = ans(:,:,1) = 0 0 0 0 0 0 0 0 0 ans(:,:,2) = 1 2 3 4 5 6 7 8 9
我們也可以使用ones()、zeros()或rand()函式建立多維陣列。
例如:
b = rand(4,3,2)
MATLAB將執行上述語句並返回以下結果:
b(:,:,1) = 0.0344 0.7952 0.6463 0.4387 0.1869 0.7094 0.3816 0.4898 0.7547 0.7655 0.4456 0.2760 b(:,:,2) = 0.6797 0.4984 0.2238 0.6551 0.9597 0.7513 0.1626 0.3404 0.2551 0.1190 0.5853 0.5060
我們還可以使用cat()函式構建多維陣列。它沿著指定的維度連線陣列列表−
cat()函式的語法為−
B = cat(dim, A1, A2...)
其中,
B是建立的新陣列
A1、A2、...是要連線的陣列
dim是沿其連線陣列的維度
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
a = [9 8 7; 6 5 4; 3 2 1]; b = [1 2 3; 4 5 6; 7 8 9]; c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])
執行檔案時,它會顯示−
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0
陣列函式
MATLAB 提供以下函式來排序、旋轉、置換、重塑或移動陣列內容。
| 函式 | 用途 |
|---|---|
| length | 向量或最大陣列維度的長度 |
| ndims | 陣列維度的數量 |
| numel | 陣列元素的數量 |
| size | 陣列維度 |
| iscolumn | 確定輸入是否為列向量 |
| isempty | 確定陣列是否為空 |
| ismatrix | 確定輸入是否為矩陣 |
| isrow | 確定輸入是否為行向量 |
| isscalar | 確定輸入是否為標量 |
| isvector | 確定輸入是否為向量 |
| blkdiag | 從輸入引數構造塊對角矩陣 |
| circshift | 迴圈移動陣列 |
| ctranspose | 複共軛轉置 |
| diag | 對角矩陣和矩陣的對角線 |
| flipdim | 沿指定維度翻轉陣列 |
| fliplr | 從左到右翻轉矩陣 |
| flipud | 從上到下翻轉矩陣 |
| ipermute | 反轉N維陣列的維度 |
| permute | 重新排列N維陣列的維度 |
| repmat | 複製和平鋪陣列 |
| reshape | 重塑陣列 |
| rot90 | 將矩陣旋轉90度 |
| shiftdim | 移動維度 |
| issorted | 確定集合元素是否按排序順序排列 |
| sort | 按升序或降序對陣列元素進行排序 |
| sortrows | 按升序對行進行排序 |
| squeeze | 刪除單一維度 |
| transpose | 轉置 |
| vectorize | 將表示式向量化 |
示例
以下示例說明了上面提到的某些函式。
長度、維度和元素數量−
建立一個指令碼檔案,並將以下程式碼輸入其中−
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9]; length(x) % length of x vector y = rand(3, 4, 5, 2); ndims(y) % no of dimensions in array y s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab']; numel(s) % no of elements in s
執行檔案時,它會顯示以下結果−
ans = 8 ans = 4 ans = 23
陣列元素的迴圈移位−
建立一個指令碼檔案,並將以下程式碼輸入其中−
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.
執行檔案時,它會顯示以下結果−
a = 1 2 3 4 5 6 7 8 9 b = 7 8 9 1 2 3 4 5 6 c = 8 9 7 2 3 1 5 6 4
排序陣列
建立一個指令碼檔案,並將以下程式碼輸入其中−
v = [ 23 45 12 9 5 0 19 17] % horizontal vector sort(v) % sorting v m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array sort(m, 1) % sorting m along the row sort(m, 2) % sorting m along the column
執行檔案時,它會顯示以下結果−
v = 23 45 12 9 5 0 19 17 ans = 0 5 9 12 17 19 23 45 m = 2 6 4 5 3 9 2 0 1 ans = 2 0 1 2 3 4 5 6 9 ans = 2 4 6 3 5 9 0 1 2
元胞陣列
元胞陣列是索引單元的陣列,其中每個單元可以儲存不同維度和資料型別的陣列。
cell函式用於建立元胞陣列。cell函式的語法為−
C = cell(dim) C = cell(dim1,...,dimN) D = cell(obj)
其中,
C是元胞陣列;
dim是標量整數或整數向量,指定元胞陣列C的維度;
dim1, ... , dimN是指定C維度的標量整數;
obj是以下之一−
- Java陣列或物件
- .NET型別為System.String或System.Object的陣列
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}
執行檔案時,它會顯示以下結果−
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}
訪問元胞陣列中的資料
有兩種方法可以引用元胞陣列的元素−
- 將索引括在第一個括號()中,以引用單元集
- 將索引括在大括號{}中,以引用單個單元中的資料
當您將索引括在第一個括號中時,它指的是單元集。
圓括號中的元胞陣列索引指的是單元集。
例如:
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)
MATLAB將執行上述語句並返回以下結果:
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}
您還可以透過使用花括號索引來訪問單元的內容。
例如:
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}
MATLAB將執行上述語句並返回以下結果:
ans = Blue ans = Green ans = Yellow
MATLAB - 冒號表示法
冒號(:)是MATLAB中最有用的運算子之一。它用於建立向量、陣列下標和指定迭代。
如果要建立一個包含從1到10的整數的行向量,您可以寫−
1:10
MATLAB執行該語句並返回一個包含從1到10的整數的行向量−
ans =
1 2 3 4 5 6 7 8 9 10
如果要指定除1以外的增量值,例如−
100: -5: 50
MATLAB執行該語句並返回以下結果−
ans = 100 95 90 85 80 75 70 65 60 55 50
讓我們再舉一個例子−
0:pi/8:pi
MATLAB執行該語句並返回以下結果−
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416
您可以使用冒號運算子建立索引向量以選擇陣列的行、列或元素。
下表描述了為此目的而使用的它(讓我們有一個矩陣A)−
| 格式 | 用途 |
|---|---|
| A(:,j) | 是A的第j列。 |
| A(i,:) | 是A的第i行。 |
| A(:,:) | 是等效的二維陣列。對於矩陣,這與A相同。 |
| A(j:k) | 是A(j)、A(j+1)、...、A(k)。 |
| A(:,j:k) | 是A(:,j)、A(:,j+1)、...、A(:,k)。 |
| A(:,:,k) | 是三維陣列A的第k頁。 |
| A(i,j,k,:) | 是四維陣列A中的一個向量。該向量包括A(i,j,k,1)、A(i,j,k,2)、A(i,j,k,3)等。 |
| A(:) | 是A的所有元素,被視為單個列。在賦值語句的左側,A(:)填充A,保留其之前的形狀。在這種情況下,右側必須包含與A相同數量的元素。 |
示例
建立一個指令碼檔案,並在其中鍵入以下程式碼−
A = [1 2 3 4; 4 5 6 7; 7 8 9 10] A(:,2) % second column of A A(:,2:3) % second and third column of A A(2:3,2:3) % second and third rows and second and third columns
執行檔案時,它會顯示以下結果−
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9
MATLAB - 數字
MATLAB 支援各種數值類,包括有符號和無符號整數以及單精度和雙精度浮點數。預設情況下,MATLAB 將所有數值儲存為雙精度浮點數。
您可以選擇將任何數字或數字陣列儲存為整數或單精度數字。
所有數值型別都支援基本陣列運算和數學運算。
轉換為各種數值資料型別
MATLAB 提供以下函式來轉換為各種數值資料型別−
| 函式 | 用途 |
|---|---|
| double | 轉換為雙精度數 |
| single | 轉換為單精度數 |
| int8 | 轉換為8位有符號整數 |
| int16 | 轉換為16位有符號整數 |
| int32 | 轉換為32位有符號整數 |
| int64 | 轉換為64位有符號整數 |
| uint8 | 轉換為8位無符號整數 |
| uint16 | 轉換為16位無符號整數 |
| uint32 | 轉換為32位無符號整數 |
| uint64 | 轉換為64位無符號整數 |
示例
建立一個指令碼檔案,並鍵入以下程式碼−
x = single([5.32 3.47 6.28]) .* 7.5 x = double([5.32 3.47 6.28]) .* 7.5 x = int8([5.32 3.47 6.28]) .* 7.5 x = int16([5.32 3.47 6.28]) .* 7.5 x = int32([5.32 3.47 6.28]) .* 7.5 x = int64([5.32 3.47 6.28]) .* 7.5
執行檔案時,它會顯示以下結果−
x = 39.900 26.025 47.100 x = 39.900 26.025 47.100 x = 38 23 45 x = 38 23 45 x = 38 23 45 x = 38 23 45
示例
讓我們再擴充套件一下前面的例子。建立一個指令碼檔案,並鍵入以下程式碼−
x = int32([5.32 3.47 6.28]) .* 7.5 x = int64([5.32 3.47 6.28]) .* 7.5 x = num2cell(x)
執行檔案時,它會顯示以下結果−
x =
38 23 45
x =
38 23 45
x =
{
[1,1] = 38
[1,2] = 23
[1,3] = 45
}
最小和最大整數
intmax()和intmin()函式返回所有型別的整數可以表示的最大值和最小值。
這兩個函式都將整數資料型別作為引數,例如intmax(int8)或intmin(int64),並返回可以使用整數資料型別表示的最大值和最小值。
示例
以下示例說明如何獲取整數的最小值和最大值。建立一個指令碼檔案,並在其中編寫以下程式碼−
% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))
執行檔案時,它會顯示以下結果−
ans = The range for int8 is: -128 to 127 ans = The range for int16 is: -32768 to 32767 ans = The range for int32 is: -2147483648 to 2147483647 ans = The range for int64 is: 0 to 0 ans = The range for uint8 is: 0 to 255 ans = The range for uint16 is: 0 to 65535 ans = The range for uint32 is: 0 to -1 ans = The range for uint64 is: 0 to 18446744073709551616
最小和最大浮點數
realmax()和realmin()函式返回可以用浮點數表示的最大值和最小值。
這兩個函式在使用引數'single'呼叫時,返回可以使用單精度資料型別表示的最大值和最小值,而在使用引數'double'呼叫時,返回可以使用雙精度資料型別表示的最大值和最小值。
示例
以下示例說明如何獲取最小和最大浮點數。建立一個指令碼檔案,並在其中編寫以下程式碼−
% displaying the smallest and largest single-precision
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
realmin('single'), realmax('single'))
% displaying the smallest and largest double-precision
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
realmin('double'), realmax('double'))
執行檔案時,它會顯示以下結果−
ans = The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38
ans = The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308
MATLAB - 字串
在 MATLAB 中建立字元陣列非常簡單。事實上,我們已經多次使用過它。例如,您可以在命令提示符中鍵入以下內容:
my_string = 'Tutorials Point'
MATLAB將執行上述語句並返回以下結果:
my_string = Tutorials Point
MATLAB 將所有變數視為陣列,字串被視為字元陣列。讓我們使用 **whos** 命令來檢查上面建立的變數:
whos
MATLAB將執行上述語句並返回以下結果:
Name Size Bytes Class Attributes my_string 1x16 32 char
有趣的是,您可以使用數值轉換函式(如 **uint8** 或 **uint16**)將字串中的字元轉換為其數值程式碼。**char** 函式將整數向量轉換回字元:
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
my_string = 'Tutorial''s Point'; str_ascii = uint8(my_string) % 8-bit ascii values str_back_to_char= char(str_ascii) str_16bit = uint16(my_string) % 16-bit ascii values str_back_to_char = char(str_16bit)
執行檔案時,它會顯示以下結果−
str_ascii = 84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116 str_back_to_char = Tutorial's Point str_16bit = 84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116 str_back_to_char = Tutorial's Point
矩形字元陣列
到目前為止,我們討論的字串是一維字元陣列;但是,我們需要儲存更多內容。我們需要在程式中儲存更多維度的文字資料。這是透過建立矩形字元陣列來實現的。
建立矩形字元陣列最簡單的方法是將兩個或多個一維字元陣列垂直或水平連線起來,具體取決於需要。
您可以透過以下任一方式垂直組合字串:
使用 MATLAB 連線運算子 **[]** 並用分號 (;) 分隔每一行。請注意,在此方法中,每一行必須包含相同數量的字元。對於長度不同的字串,應根據需要用空格字元填充。
使用 **char** 函式。如果字串長度不同,char 會用尾隨空格填充較短的字串,以便每一行具有相同數量的字元。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
doc_profile = ['Zara Ali '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')
執行檔案時,它會顯示以下結果−
doc_profile = Zara Ali Sr. Surgeon R N Tagore Cardiology Research Center doc_profile = Zara Ali Sr. Surgeon RN Tagore Cardiology Research Center
您可以透過以下任一方式水平組合字串:
使用 MATLAB 連線運算子 **[]** 並用逗號或空格分隔輸入字串。此方法保留輸入陣列中的任何尾隨空格。
使用字串連線函式 **strcat**。此方法會刪除輸入中的尾隨空格。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
name = 'Zara Ali '; position = 'Sr. Surgeon '; worksAt = 'R N Tagore Cardiology Research Center'; profile = [name ', ' position ', ' worksAt] profile = strcat(name, ', ', position, ', ', worksAt)
執行檔案時,它會顯示以下結果−
profile = Zara Ali , Sr. Surgeon , R N Tagore Cardiology Research Center profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center
將字串組合到元胞陣列中
從我們之前的討論中可以清楚地看出,組合長度不同的字串可能很麻煩,因為陣列中的所有字串都必須具有相同的長度。我們已在字串末尾使用空格來使它們的長度相等。
但是,組合字串的更有效方法是將結果陣列轉換為元胞陣列。
MATLAB 元胞陣列可以在陣列中儲存不同大小和型別的數。元胞陣列提供了一種更靈活的方式來儲存不同長度的字串。
**cellstr** 函式將字元陣列轉換為字串的元胞陣列。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
name = 'Zara Ali '; position = 'Sr. Surgeon '; worksAt = 'R N Tagore Cardiology Research Center'; profile = char(name, position, worksAt); profile = cellstr(profile); disp(profile)
執行檔案時,它會顯示以下結果−
{
[1,1] = Zara Ali
[2,1] = Sr. Surgeon
[3,1] = R N Tagore Cardiology Research Center
}
MATLAB 中的字串函式
MATLAB 提供了許多用於建立、組合、解析、比較和操作字串的字串函式。
下表簡要描述了 MATLAB 中的字串函式:
| 函式 | 用途 |
|---|---|
| 用於在字元陣列中儲存文字、組合字元陣列等的函式。 | |
| blanks | 建立空格字元字串 |
| cellstr | 從字元陣列建立字串的元胞陣列 |
| char | 轉換為字元陣列(字串) |
| iscellstr | 確定輸入是否為字串的元胞陣列 |
| ischar | 確定專案是否為字元陣列 |
| sprintf | 將資料格式化為字串 |
| strcat | 水平連線字串 |
| strjoin | 將元胞陣列中的字串連線成單個字串 |
| 用於識別字符串部分、查詢和替換子字串的函式 | |
| ischar | 確定專案是否為字元陣列 |
| isletter | 字母字元的陣列元素 |
| isspace | 空格字元的陣列元素 |
| isstrprop | 確定字串是否屬於指定類別 |
| sscanf | 從字串讀取格式化資料 |
| strfind | 在一個字串中查詢另一個字串 |
| strrep | 查詢和替換子字串 |
| strsplit | 在指定分隔符處分割字串 |
| strtok | 字串的選定部分 |
| validatestring | 檢查文字字串的有效性 |
| symvar | 確定表示式中的符號變數 |
| regexp | 匹配正則表示式(區分大小寫) |
| regexpi | 匹配正則表示式(不區分大小寫) |
| regexprep | 使用正則表示式替換字串 |
| regexptranslate | 將字串轉換為正則表示式 |
| 用於字串比較的函式 | |
| strcmp | 比較字串(區分大小寫) |
| strcmpi | 比較字串(不區分大小寫) |
| strncmp | 比較字串的前 n 個字元(區分大小寫) |
| strncmpi | 比較字串的前 n 個字元(不區分大小寫) |
| 用於將字串更改為大寫或小寫、建立或刪除空格的函式 | |
| deblank | 從字串末尾刪除尾隨空格 |
| strtrim | 刪除字串開頭和結尾的空格 |
| lower | 將字串轉換為小寫 |
| upper | 將字串轉換為大寫 |
| strjust | 調整字元陣列 |
示例
以下示例說明了一些上述字串函式:
格式化字串
建立一個指令碼檔案,並將以下程式碼輸入其中−
A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)
執行檔案時,它會顯示以下結果−
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59
連線字串
建立一個指令碼檔案,並將以下程式碼輸入其中−
%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};
% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")
執行檔案時,它會顯示以下結果−
str1 = red-blue-green-yellow-orange str2 = red,blue,green,yellow,orange
查詢和替換字串
建立一個指令碼檔案,並將以下程式碼輸入其中−
students = {'Zara Ali', 'Neha Bhatnagar', ...
'Monica Malik', 'Madhu Gautam', ...
'Madhu Sharma', 'Bhawna Sharma',...
'Nuha Ali', 'Reva Dutta', ...
'Sunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)
執行檔案時,它會顯示以下結果−
new_student =
{
[1,1] = Poulomi Dutta
}
first_names =
{
[1,1] = Zara
[1,2] = Neha
[1,3] = Monica
[1,4] = Madhu
[1,5] = Madhu
[1,6] = Bhawna
[1,7] = Nuha
[1,8] = Reva
[1,9] = Sunaina
[1,10] = Sofia
}
比較字串
建立一個指令碼檔案,並將以下程式碼輸入其中−
str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
sprintf('%s and %s are equal', str1, str2)
else
sprintf('%s and %s are not equal', str1, str2)
end
執行檔案時,它會顯示以下結果−
str1 = This is test str2 = This is text ans = This is test and This is text are not equal
MATLAB - 函式
函式是一組一起執行任務的語句。在 MATLAB 中,函式在單獨的檔案中定義。檔案和函式的名稱應相同。
函式在其自己的工作區(也稱為 **區域性工作區**)中操作變數,該工作區與您在 MATLAB 命令提示符下訪問的工作區(稱為 **基本工作區**)分開。
函式可以接受多個輸入引數,並且可以返回多個輸出引數。
函式語句的語法為:
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)
示例
名為 *mymax* 的以下函式應寫入名為 *mymax.m* 的檔案中。它以五個數字作為引數,並返回這些數字中的最大值。
建立一個名為 mymax.m 的函式檔案,並在其中鍵入以下程式碼:
function max = mymax(n1, n2, n3, n4, n5) %This function calculates the maximum of the % five numbers given as input max = n1; if(n2 > max) max = n2; end if(n3 > max) max = n3; end if(n4 > max) max = n4; end if(n5 > max) max = n5; end
函式的第一行以關鍵字 **function** 開頭。它給出函式的名稱和引數的順序。在我們的示例中,*mymax* 函式有五個輸入引數和一個輸出引數。
緊跟在函式語句之後的註釋行提供幫助文字。當您鍵入以下內容時,將列印這些行:
help mymax
MATLAB將執行上述語句並返回以下結果:
This function calculates the maximum of the five numbers given as input
您可以這樣呼叫函式:
mymax(34, 78, 89, 23, 11)
MATLAB將執行上述語句並返回以下結果:
ans = 89
匿名函式
匿名函式類似於傳統程式語言中的行內函數,在單個 MATLAB 語句中定義。它包含一個 MATLAB 表示式和任意數量的輸入和輸出引數。
您可以在 MATLAB 命令列或函式或指令碼中定義匿名函式。
這樣,您就可以建立簡單的函式,而無需為它們建立檔案。
從表示式建立匿名函式的語法為
f = @(arglist)expression
示例
在此示例中,我們將編寫一個名為 power 的匿名函式,它將以兩個數字作為輸入,並返回第一個數字的第二個數字次冪。
建立一個指令碼檔案,並在其中鍵入以下程式碼−
power = @(x, n) x.^n; result1 = power(7, 3) result2 = power(49, 0.5) result3 = power(10, -10) result4 = power (4.5, 1.5)
執行檔案時,它會顯示−
result1 = 343 result2 = 7 result3 = 1.0000e-10 result4 = 9.5459
主函式和子函式
除匿名函式之外的任何函式都必須在檔案中定義。每個函式檔案都包含一個必需的主函式(首先出現)和任意數量的可選子函式(出現在主函式之後並由其使用)。
主函式可以從定義它們的外部檔案呼叫,無論是從命令列還是從其他函式呼叫,但子函式不能從命令列或其他函式呼叫,不能在函式檔案外部呼叫。
子函式僅對定義它們的函式檔案中的主函式和其他子函式可見。
示例
讓我們編寫一個名為 quadratic 的函式,該函式將計算二次方程的根。該函式將接收三個輸入,即二次係數、線性係數和常數項。它將返回根。
函式檔案 quadratic.m 將包含主函式 *quadratic* 和子函式 *disc*,後者計算判別式。
建立一個函式檔案 *quadratic.m*,並在其中鍵入以下程式碼:
function [x1,x2] = quadratic(a,b,c) %this function returns the roots of % a quadratic equation. % It takes 3 input arguments % which are the co-efficients of x2, x and the %constant term % It returns the roots d = disc(a,b,c); x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of quadratic function dis = disc(a,b,c) %function calculates the discriminant dis = sqrt(b^2 - 4*a*c); end % end of sub-function
您可以從命令提示符處呼叫上述函式,如下所示:
quadratic(2,4,-4)
MATLAB將執行上述語句並返回以下結果:
ans = 0.7321
巢狀函式
您可以在另一個函式的主體中定義函式。這些稱為巢狀函式。巢狀函式包含任何其他函式的任何或所有元件。
巢狀函式在另一個函式的作用域內定義,並且它們共享對包含函式工作區的訪問許可權。
巢狀函式遵循以下語法:
function x = A(p1, p2) ... B(p2) function y = B(p3) ... end ... end
示例
讓我們重寫上一個示例中的 *quadratic* 函式,但是,這次 disc 函式將是一個巢狀函式。
建立一個函式檔案 *quadratic2.m*,並在其中鍵入以下程式碼:
function [x1,x2] = quadratic2(a,b,c) function disc % nested function d = sqrt(b^2 - 4*a*c); end % end of function disc disc; x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of function quadratic2
您可以從命令提示符處呼叫上述函式,如下所示:
quadratic2(2,4,-4)
MATLAB將執行上述語句並返回以下結果:
ans = 0.73205
私有函式
私有函式是一個主函式,它僅對有限數量的其他函式可見。如果您不想公開函式的實現,則可以將其建立為私有函式。
私有函式駐留在名稱為 **private** 的 **子資料夾** 中。
它們僅對父資料夾中的函式可見。
示例
讓我們重寫 *quadratic* 函式。但是,這次計算判別式的 *disc* 函式將是一個私有函式。
在工作目錄中建立一個名為 private 的子資料夾。將以下函式檔案 *disc.m* 儲存在其中:
function dis = disc(a,b,c) %function calculates the discriminant dis = sqrt(b^2 - 4*a*c); end % end of sub-function
在您的工作目錄中建立一個函式 quadratic3.m,並在其中鍵入以下程式碼:
function [x1,x2] = quadratic3(a,b,c) %this function returns the roots of % a quadratic equation. % It takes 3 input arguments % which are the co-efficient of x2, x and the %constant term % It returns the roots d = disc(a,b,c); x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of quadratic3
您可以從命令提示符處呼叫上述函式,如下所示:
quadratic3(2,4,-4)
MATLAB將執行上述語句並返回以下結果:
ans = 0.73205
全域性變數
全域性變數可以被多個函式共享。為此,您需要在所有函式中將變數宣告為全域性變數。
如果要從基本工作區訪問該變數,則在命令列中宣告該變數。
全域性宣告必須在函式中實際使用變數之前發生。最好對全域性變數的名稱使用大寫字母,以將其與其他變數區分開來。
示例
讓我們建立一個名為 average.m 的函式檔案,並在其中鍵入以下程式碼:
function avg = average(nums) global TOTAL avg = sum(nums)/TOTAL; end
建立一個指令碼檔案,並在其中鍵入以下程式碼−
global TOTAL; TOTAL = 10; n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42]; av = average(n)
執行該檔案時,它將顯示以下結果:
av = 35.500
MATLAB - 資料匯入
在 MATLAB 中匯入資料意味著從外部檔案載入資料。**importdata** 函式允許載入各種不同格式的資料檔案。它具有以下五種形式:
| 序號 | 函式 & 描述 |
|---|---|
| 1 |
A = importdata(filename) 從 *filename* 表示的檔案將資料載入到陣列 A 中。 |
| 2 |
A = importdata('-pastespecial') 從系統剪貼簿而不是從檔案載入資料。 |
| 3 |
A = importdata(___, delimiterIn) 將 *delimiterIn* 解釋為 ASCII 檔案、filename 或剪貼簿資料中的列分隔符。您可以將 *delimiterIn* 與上述語法中的任何輸入引數一起使用。 |
| 4 |
A = importdata(___, delimiterIn, headerlinesIn) 從 ASCII 檔案、filename 或剪貼簿載入資料,從第 *headerlinesIn+1* 行開始讀取數值資料。 |
| 5 |
[A, delimiterOut, headerlinesOut] = importdata(___) 使用先前語法中的任何輸入引數,在 *delimiterOut* 中返回輸入 ASCII 檔案的檢測到的分隔符字元,並在 *headerlinesOut* 中返回檢測到的標題行數。 |
預設情況下,Octave 不支援 *importdata()* 函式,因此您需要搜尋並安裝此軟體包才能使以下示例與您的 Octave 安裝一起使用。
示例 1
讓我們載入並顯示一個影像檔案。建立一個指令碼檔案,並在其中鍵入以下程式碼:
filename = 'smile.jpg'; A = importdata(filename); image(A);
執行該檔案時,MATLAB 會顯示影像檔案。但是,您必須將其儲存在當前目錄中。

示例 2
在此示例中,我們匯入一個文字檔案並指定分隔符和列標題。讓我們建立一個以空格分隔的帶列標題的 ASCII 檔案,命名為 *weeklydata.txt*。
我們的文字檔案 weeklydata.txt 如下所示:
SunDay MonDay TuesDay WednesDay ThursDay FriDay SaturDay 95.01 76.21 61.54 40.57 55.79 70.28 81.53 73.11 45.65 79.19 93.55 75.29 69.87 74.68 60.68 41.85 92.18 91.69 81.32 90.38 74.51 48.60 82.14 73.82 41.03 0.99 67.22 93.18 89.13 44.47 57.63 89.36 13.89 19.88 46.60
建立一個指令碼檔案,並在其中鍵入以下程式碼−
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
end
執行檔案時,它會顯示以下結果−
SunDay 95.0100 73.1100 60.6800 48.6000 89.1300 MonDay 76.2100 45.6500 41.8500 82.1400 44.4700 TuesDay 61.5400 79.1900 92.1800 73.8200 57.6300 WednesDay 40.5700 93.5500 91.6900 41.0300 89.3600 ThursDay 55.7900 75.2900 81.3200 0.9900 13.8900 FriDay 70.2800 69.8700 90.3800 67.2200 19.8800 SaturDay 81.5300 74.6800 74.5100 93.1800 46.6000
示例 3
在此示例中,讓我們從剪貼簿匯入資料。
將以下行復制到剪貼簿:
數學很簡單
建立一個指令碼檔案,並鍵入以下程式碼−
A = importdata('-pastespecial')
執行檔案時,它會顯示以下結果−
A = 'Mathematics is simple'
低階檔案 I/O
importdata 函式是一個高階函式。MATLAB 中的低階檔案 I/O 函式允許對讀取或寫入檔案的資料進行最精細的控制。但是,這些函式需要有關檔案的更多詳細資訊才能有效地工作。
MATLAB 提供以下函式用於位元組或字元級別的讀寫操作:
| 函式 | 描述 |
|---|---|
| fclose | 關閉一個或所有開啟的檔案 |
| feof | 測試檔案結束 |
| ferror | 檔案 I/O 錯誤資訊 |
| fgetl | 從檔案中讀取一行,刪除換行符 |
| fgets | 從檔案中讀取一行,保留換行符 |
| fopen | 開啟檔案或獲取有關開啟檔案的資訊 |
| fprintf | 將資料寫入文字檔案 |
| fread | 從二進位制檔案讀取資料 |
| frewind | 將檔案位置指示器移動到開啟檔案的開頭 |
| fscanf | 從文字檔案讀取資料 |
| fseek | 移動到檔案中的指定位置 |
| ftell | 開啟檔案中的位置 |
| fwrite | 將資料寫入二進位制檔案 |
使用低階 I/O 匯入文字資料檔案
MATLAB 提供以下函式用於文字資料檔案的低階匯入:
fscanf 函式讀取文字或 ASCII 檔案中的格式化資料。
fgetl 和 fgets 函式每次讀取檔案的一行,其中換行符分隔每一行。
fread 函式以位元組或位級別讀取資料流。
示例
我們在工作目錄中儲存了一個名為“myfile.txt”的文字資料檔案。該檔案儲存了 2012 年 6 月、7 月和 8 月三個月的降雨資料。
myfile.txt 中的資料包含五個地點重複的時間、月份和降雨量測量值集。標題資料儲存月份數 M;因此我們有 M 個測量值集。
檔案如下所示:
Rainfall Data Months: June, July, August M = 3 12:00:00 June-2012 17.21 28.52 39.78 16.55 23.67 19.15 0.35 17.57 NaN 12.01 17.92 28.49 17.40 17.06 11.09 9.59 9.33 NaN 0.31 0.23 10.46 13.17 NaN 14.89 19.33 20.97 19.50 17.65 14.45 14.00 18.23 10.34 17.95 16.46 19.34 09:10:02 July-2012 12.76 16.94 14.38 11.86 16.89 20.46 23.17 NaN 24.89 19.33 30.97 49.50 47.65 24.45 34.00 18.23 30.34 27.95 16.46 19.34 30.46 33.17 NaN 34.89 29.33 30.97 49.50 47.65 24.45 34.00 28.67 30.34 27.95 36.46 29.34 15:03:40 August-2012 17.09 16.55 19.59 17.25 19.22 17.54 11.45 13.48 22.55 24.01 NaN 21.19 25.85 25.05 27.21 26.79 24.98 12.23 16.99 18.67 17.54 11.45 13.48 22.55 24.01 NaN 21.19 25.85 25.05 27.21 26.79 24.98 12.23 16.99 18.67
我們將從該檔案匯入資料並顯示此資料。請執行以下步驟:
使用 fopen 函式開啟檔案並獲取檔案識別符號。
使用 格式說明符(例如字串的“%s”、整數的“%d”或浮點數的“%f”)描述檔案中的資料。
要跳過檔案中的文字字元,請將它們包含在格式描述中。要跳過資料欄位,請在說明符中使用星號(“*”)。
例如,要讀取標題並返回 M 的單個值,我們編寫:
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
預設情況下,fscanf 會根據我們的格式描述讀取資料,直到它找不到任何匹配的資料,或者到達檔案末尾。這裡我們將使用 for 迴圈讀取 3 組資料,每次讀取 7 行 5 列。
我們將在工作區中建立一個名為 mydata 的結構來儲存從檔案中讀取的資料。該結構具有三個欄位 - time、month 和 raindata 陣列。
建立一個指令碼檔案,並在其中鍵入以下程式碼−
filename = '/data/myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);
執行檔案時,它會顯示以下結果−
12:00:00 June-2012 17.2100 17.5700 11.0900 13.1700 14.4500 28.5200 NaN 9.5900 NaN 14.0000 39.7800 12.0100 9.3300 14.8900 18.2300 16.5500 17.9200 NaN 19.3300 10.3400 23.6700 28.4900 0.3100 20.9700 17.9500 19.1500 17.4000 0.2300 19.5000 16.4600 0.3500 17.0600 10.4600 17.6500 19.3400 09:10:02 July-2012 12.7600 NaN 34.0000 33.1700 24.4500 16.9400 24.8900 18.2300 NaN 34.0000 14.3800 19.3300 30.3400 34.8900 28.6700 11.8600 30.9700 27.9500 29.3300 30.3400 16.8900 49.5000 16.4600 30.9700 27.9500 20.4600 47.6500 19.3400 49.5000 36.4600 23.1700 24.4500 30.4600 47.6500 29.3400 15:03:40 August-2012 17.0900 13.4800 27.2100 11.4500 25.0500 16.5500 22.5500 26.7900 13.4800 27.2100 19.5900 24.0100 24.9800 22.5500 26.7900 17.2500 NaN 12.2300 24.0100 24.9800 19.2200 21.1900 16.9900 NaN 12.2300 17.5400 25.8500 18.6700 21.1900 16.9900 11.4500 25.0500 17.5400 25.8500 18.6700
MATLAB - 資料輸出
MATLAB 中的資料匯出(或輸出)意味著寫入檔案。MATLAB 允許您在讀取 ASCII 檔案的其他應用程式中使用您的資料。為此,MATLAB 提供了多種資料匯出選項。
您可以建立以下型別的檔案:
來自陣列的矩形、分隔的 ASCII 資料檔案。
鍵擊和生成的文字輸出的日記(或日誌)檔案。
使用低階函式(如 fprintf)的專用 ASCII 檔案。
MEX 檔案以訪問寫入特定文字檔案格式的 C/C++ 或 Fortran 例程。
除此之外,您還可以將資料匯出到電子表格。
有兩種方法可以將數值陣列匯出為分隔的 ASCII 資料檔案:
使用 save 函式並指定 -ascii 限定符
使用 dlmwrite 函式
使用 save 函式的語法為:
save my_data.out num_array -ascii
其中,my_data.out 是建立的分隔的 ASCII 資料檔案,num_array 是數值陣列,−ascii 是說明符。
使用 dlmwrite 函式的語法為:
dlmwrite('my_data.out', num_array, 'dlm_char')
其中,my_data.out 是建立的分隔的 ASCII 資料檔案,num_array 是數值陣列,dlm_char 是分隔符字元。
示例
以下示例演示了該概念。建立一個指令碼檔案並鍵入以下程式碼:
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out
執行檔案時,它會顯示以下結果−
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00 1 2 3 4 4 5 6 7 7 8 9 0
請注意,save -ascii 命令和 dlmwrite 函式不適用於單元陣列作為輸入。要從單元陣列的內容建立分隔的 ASCII 檔案,您可以
或者,使用 cell2mat 函式將單元陣列轉換為矩陣
或者使用低階檔案 I/O 函式匯出單元陣列。
如果使用 save 函式將字元陣列寫入 ASCII 檔案,它會將字元的 ASCII 等效項寫入檔案。
例如,讓我們將單詞“hello”寫入檔案:
h = 'hello'; save textdata.out h -ascii type textdata.out
MATLAB 執行上述語句並顯示以下結果。即字串“hello”的字元以 8 位 ASCII 格式顯示。
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02
寫入日記檔案
日記檔案是 MATLAB 會話的活動日誌。diary 函式在磁碟檔案中建立會話的精確副本,但不包括圖形。
要開啟 diary 函式,請鍵入:
diary
可選地,您可以給出日誌檔案的名稱,例如:
diary logdata.out
要關閉 diary 函式:
diary off
您可以在文字編輯器中開啟日記檔案。
使用低階 I/O 將資料匯出到文字資料檔案
到目前為止,我們已經匯出了數值陣列。但是,您可能需要建立其他文字檔案,包括數值和字元資料的組合、非矩形輸出檔案或使用非 ASCII 編碼方案的檔案。為此,MATLAB 提供了低階 fprintf 函式。
與低階 I/O 檔案活動一樣,在匯出之前,您需要使用 fopen 函式開啟或建立檔案並獲取檔案識別符號。預設情況下,fopen 以只讀方式開啟檔案。您應該指定寫入或追加的許可權,例如“w”或“a”。
處理完檔案後,您需要使用 fclose(fid) 函式關閉它。
以下示例演示了該概念:
示例
建立一個指令碼檔案,並在其中鍵入以下程式碼−
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function\n\n');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f\n', y);
fclose(fid);
% display the file created
type logtable.txt
執行檔案時,它會顯示以下結果−
Log Function 0.000000 -Inf 10.000000 2.302585 20.000000 2.995732 30.000000 3.401197 40.000000 3.688879 50.000000 3.912023 60.000000 4.094345 70.000000 4.248495 80.000000 4.382027 90.000000 4.499810 100.000000 4.605170
MATLAB - 繪圖
要繪製函式的圖形,您需要執行以下步驟:
定義 x,指定變數 x 的 值範圍,在此範圍內要繪製函式
定義函式 y = f(x)
呼叫 plot 命令,如 plot(x, y)
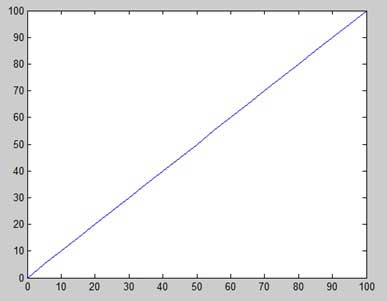
以下示例將演示該概念。讓我們繪製從 0 到 100 的 x 值範圍內的簡單函式 y = x,增量為 5。
建立一個指令碼檔案,並鍵入以下程式碼−
x = [0:5:100]; y = x; plot(x, y)
執行檔案時,MATLAB 將顯示以下圖形:
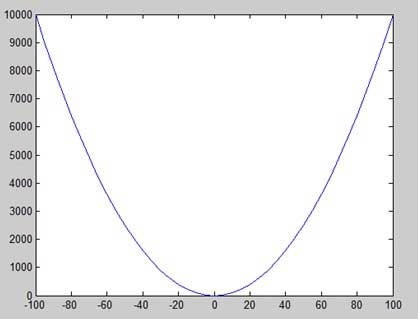
讓我們再舉一個繪製函式 y = x2 的例子。在此示例中,我們將繪製兩個具有相同函式的圖形,但在第二次繪製時,我們將減少增量值。請注意,隨著我們減少增量,圖形變得更平滑。
建立一個指令碼檔案,並鍵入以下程式碼−
x = [1 2 3 4 5 6 7 8 9 10]; x = [-100:20:100]; y = x.^2; plot(x, y)
執行檔案時,MATLAB 將顯示以下圖形:
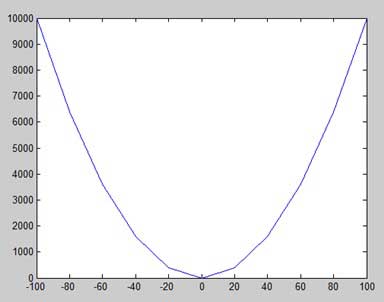
稍微修改程式碼檔案,將增量減少到 5:
x = [-100:5:100]; y = x.^2; plot(x, y)
MATLAB 繪製了一個更平滑的圖形:
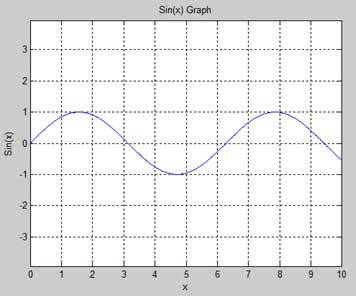
在圖形上新增標題、標籤、網格線和縮放
MATLAB 允許您新增標題、沿 x 軸和 y 軸的標籤、網格線以及調整軸以美化圖形。
xlabel 和 ylabel 命令在 x 軸和 y 軸上生成標籤。
title 命令允許您在圖形上放置標題。
grid on 命令允許您在圖形上放置網格線。
axis equal 命令允許使用相同的比例因子和兩個軸上的空間生成圖形。
axis square 命令生成一個正方形圖形。
示例
建立一個指令碼檔案,並鍵入以下程式碼−
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal
MATLAB 生成以下圖形:
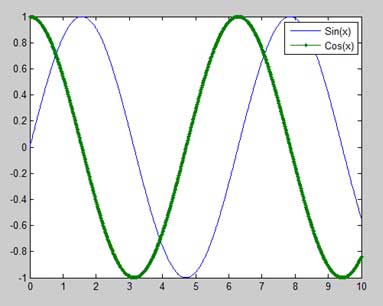
在同一圖形上繪製多個函式
您可以在同一圖形上繪製多個圖形。以下示例演示了該概念:
示例
建立一個指令碼檔案,並鍵入以下程式碼−
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')
MATLAB 生成以下圖形:
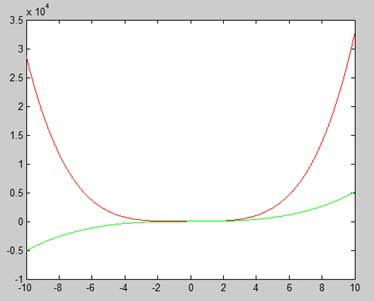
在圖形上設定顏色
MATLAB 提供了八種基本顏色選項用於繪製圖形。下表顯示了顏色及其程式碼:
| 程式碼 | 顏色 |
|---|---|
| w | 白色 |
| k | 黑色 |
| b | 藍色 |
| r | 紅色 |
| c | 青色 |
| g | 綠色 |
| m | 品紅色 |
| y | 黃色 |
示例
讓我們繪製兩個多項式的圖形
f(x) = 3x4 + 2x3+ 7x2 + 2x + 9 和
g(x) = 5x3 + 9x + 2
建立一個指令碼檔案,並鍵入以下程式碼−
x = [-10 : 0.01: 10]; y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9; g = 5 * x.^3 + 9 * x + 2; plot(x, y, 'r', x, g, 'g')
執行檔案時,MATLAB 將生成以下圖形:
設定軸刻度
axis 命令允許您設定軸刻度。您可以使用以下方式的 axis 命令為 x 軸和 y 軸提供最小值和最大值:
axis ( [xmin xmax ymin ymax] )
以下示例說明了這一點:
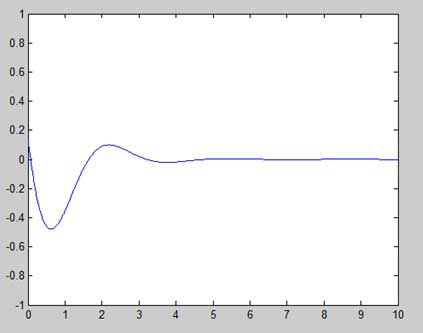
示例
建立一個指令碼檔案,並鍵入以下程式碼−
x = [0 : 0.01: 10]; y = exp(-x).* sin(2*x + 3); plot(x, y), axis([0 10 -1 1])
執行檔案時,MATLAB 將生成以下圖形:
生成子圖
當您在同一圖形中建立一系列圖形時,這些圖形中的每一個都稱為子圖。subplot 命令用於建立子圖。
該命令的語法為:
subplot(m, n, p)
其中,m 和 n 是圖形陣列的行數和列數,p 指定放置特定圖形的位置。
使用 subplot 命令建立的每個圖形都可以具有自己的特性。以下示例演示了該概念:
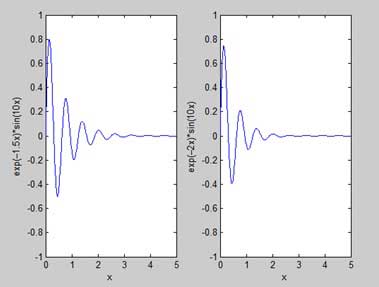
示例
讓我們生成兩個圖形:
y = e−1.5xsin(10x)
y = e−2xsin(10x)
建立一個指令碼檔案,並鍵入以下程式碼−
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])
執行檔案時,MATLAB 將生成以下圖形:
MATLAB - 圖形
本章將繼續探索 MATLAB 的繪圖和圖形功能。我們將討論:
- 繪製條形圖
- 繪製等值線
- 三維圖形
繪製條形圖
bar 命令繪製二維條形圖。讓我們舉一個例子來演示這個想法。
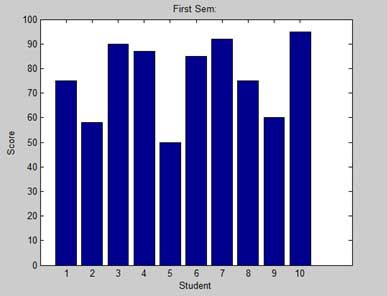
示例
讓我們假設一個有 10 名學生的虛擬教室。我們知道這些學生獲得的分數百分比分別為 75、58、90、87、50、85、92、75、60 和 95。我們將為這些資料繪製條形圖。
建立一個指令碼檔案,並鍵入以下程式碼−
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps
執行檔案時,MATLAB 將顯示以下條形圖:
繪製等值線
雙變數函式的等值線是函式具有恆定值的曲線。等值線用於透過連線高於給定水平(例如平均海平面)的相同高度的點來建立等高線圖。
MATLAB 提供了一個 contour 函式用於繪製等高線圖。
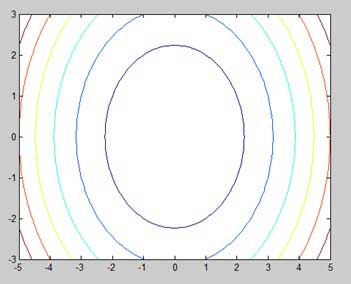
示例
讓我們生成一個等高線圖,顯示給定函式 g = f(x, y) 的等值線。此函式有兩個變數。因此,我們將不得不生成兩個自變數,即兩個資料集 x 和 y。這是透過呼叫 meshgrid 命令完成的。
meshgrid 命令用於生成元素矩陣,這些元素給出 x 和 y 上的範圍以及每種情況下增量的規範。
讓我們繪製我們的函式 g = f(x, y),其中 −5 ≤ x ≤ 5,−3 ≤ y ≤ 3。讓我們為這兩個值取 0.1 的增量。變數設定為:
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);
最後,我們需要分配函式。讓我們的函式為:x2 + y2
建立一個指令碼檔案,並鍵入以下程式碼−
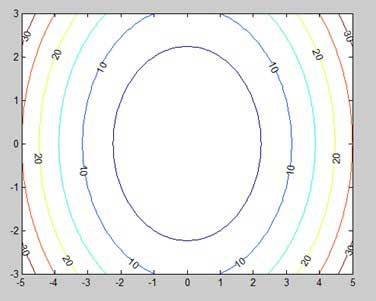
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function contour(x,y,g) % call the contour function print -deps graph.eps
執行檔案時,MATLAB 將顯示以下等高線圖:
讓我們稍微修改一下程式碼以美化地圖
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function [C, h] = contour(x,y,g); % call the contour function set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2) print -deps graph.eps
執行檔案時,MATLAB 將顯示以下等高線圖:
三維圖形
三維圖形基本上顯示由雙變數函式 g = f (x,y) 定義的曲面。
和之前一樣,為了定義g,我們首先使用**meshgrid**命令在函式的定義域上建立一組(x,y)點。接下來,我們賦值給函式本身。最後,我們使用**surf**命令建立一個曲面圖。
以下示例演示了該概念:
示例
讓我們為函式g = xe-(x2 + y2)建立一個3D曲面圖。
建立一個指令碼檔案,並鍵入以下程式碼−
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
當你執行檔案時,MATLAB將顯示以下3D圖 -
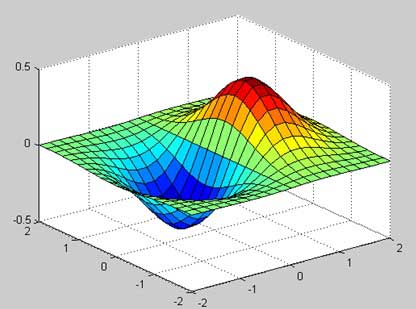
你也可以使用**mesh**命令生成三維曲面。但是,**surf**命令以彩色顯示連線線和曲面的面,而**mesh**命令建立一個線框曲面,用彩色線連線定義點。
MATLAB - 代數
到目前為止,我們已經看到所有示例都可以在MATLAB及其GNU版本(也稱為Octave)中執行。但是對於求解基本代數方程,MATLAB和Octave略有不同,因此我們將嘗試在單獨的部分中介紹MATLAB和Octave。
我們還將討論代數表示式的因式分解和化簡。
在MATLAB中求解基本代數方程
**solve**函式用於求解代數方程。在其最簡單的形式中,solve函式將用引號括起來的方程作為引數。
例如,讓我們求解方程x-5 = 0中的x。
solve('x-5=0')
MATLAB將執行上述語句並返回以下結果:
ans = 5
你也可以這樣呼叫solve函式 -
y = solve('x-5 = 0')
MATLAB將執行上述語句並返回以下結果:
y = 5
你甚至可以不包含方程的右側 -
solve('x-5')
MATLAB將執行上述語句並返回以下結果:
ans = 5
如果方程包含多個符號,那麼MATLAB預設情況下假設你正在求解x,但是,solve函式還有另一種形式 -
solve(equation, variable)
其中,你也可以提及變數。
例如,讓我們求解方程v – u – 3t2 = 0關於v的解。在這種情況下,我們應該寫 -
solve('v-u-3*t^2=0', 'v')
MATLAB將執行上述語句並返回以下結果:
ans = 3*t^2 + u
在Octave中求解基本代數方程
**roots**函式用於在Octave中求解代數方程,你可以將上述示例寫成如下形式 -
例如,讓我們求解方程x-5 = 0中的x。
roots([1, -5])
Octave將執行上述語句並返回以下結果 -
ans = 5
你也可以這樣呼叫solve函式 -
y = roots([1, -5])
Octave將執行上述語句並返回以下結果 -
y = 5
在MATLAB中求解二次方程
**solve**函式也可以求解高階方程。它通常用於求解二次方程。該函式將方程的根返回到一個數組中。
以下示例求解二次方程x2 -7x +12 = 0。建立一個指令碼檔案並輸入以下程式碼 -
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
執行檔案時,它會顯示以下結果−
The first root is: 3 The second root is: 4
在Octave中求解二次方程
以下示例在Octave中求解二次方程x2 -7x +12 = 0。建立一個指令碼檔案並輸入以下程式碼 -
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
執行檔案時,它會顯示以下結果−
The first root is: 4 The second root is: 3
在MATLAB中求解高階方程
**solve**函式也可以求解高階方程。例如,讓我們求解三次方程(x-3)2(x-7) = 0。
solve('(x-3)^2*(x-7)=0')
MATLAB將執行上述語句並返回以下結果:
ans = 3 3 7
對於高階方程,根很長,包含很多項。你可以透過將它們轉換為double來獲取這些根的數值。以下示例求解四次方程x4 − 7x3 + 3x2 − 5x + 9 = 0。
建立一個指令碼檔案,並鍵入以下程式碼−
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));
當你執行檔案時,它將返回以下結果 -
The first root is: 6.630396332390718431485053218985 The second root is: 1.0597804633025896291682772499885 The third root is: - 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i The fourth root is: - 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i Numeric value of first root 6.6304 Numeric value of second root 1.0598 Numeric value of third root -0.3451 - 1.0778i Numeric value of fourth root -0.3451 + 1.0778i
請注意,最後兩個根是複數。
在Octave中求解高階方程
以下示例求解四次方程x4 − 7x3 + 3x2 − 5x + 9 = 0。
建立一個指令碼檔案,並鍵入以下程式碼−
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));
當你執行檔案時,它將返回以下結果 -
Numeric value of first root 6.6304 Numeric value of second root -0.34509 + 1.07784i Numeric value of third root -0.34509 - 1.07784i Numeric value of fourth root 1.0598
在MATLAB中求解方程組
**solve**函式還可以用來生成包含多個變數的方程組的解。讓我們舉一個簡單的例子來演示這種用法。
讓我們求解以下方程 -
5x + 9y = 5
3x – 6y = 4
建立一個指令碼檔案,並鍵入以下程式碼−
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.y
執行檔案時,它會顯示以下結果−
ans = 22/19 ans = -5/57
同樣地,你可以求解更大的線性系統。考慮以下方程組 -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
在Octave中求解方程組
我們有一個稍微不同的方法來求解'n'個未知數的'n'個線性方程組。讓我們舉一個簡單的例子來演示這種用法。
讓我們求解以下方程 -
5x + 9y = 5
3x – 6y = 4
這樣的線性方程組可以寫成單個矩陣方程Ax = b,其中A是係數矩陣,b是包含線性方程右側的列向量,x是表示解的列向量,如下面的程式所示 -
建立一個指令碼檔案,並鍵入以下程式碼−
A = [5, 9; 3, -6]; b = [5;4]; A \ b
執行檔案時,它會顯示以下結果−
ans = 1.157895 -0.087719
同樣地,你可以求解如下所示的更大的線性系統 -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
在MATLAB中展開和收集方程
**expand**和**collect**函式分別展開和收集方程。以下示例演示了這些概念 -
當你使用許多符號函式時,你應該宣告你的變數是符號變數。
建立一個指令碼檔案,並鍵入以下程式碼−
syms x %symbolic variable x syms y %symbolic variable x % expanding equations expand((x-5)*(x+9)) expand((x+2)*(x-3)*(x-5)*(x+7)) expand(sin(2*x)) expand(cos(x+y)) % collecting equations collect(x^3 *(x-7)) collect(x^4*(x-3)*(x-5))
執行檔案時,它會顯示以下結果−
ans = x^2 + 4*x - 45 ans = x^4 + x^3 - 43*x^2 + 23*x + 210 ans = 2*cos(x)*sin(x) ans = cos(x)*cos(y) - sin(x)*sin(y) ans = x^4 - 7*x^3 ans = x^6 - 8*x^5 + 15*x^4
在Octave中展開和收集方程
你需要安裝**symbolic**包,它提供了**expand**和**collect**函式,分別用於展開和收集方程。以下示例演示了這些概念 -
當你使用許多符號函式時,你應該宣告你的變數是符號變數,但Octave定義符號變數的方法不同。注意**Sin**和**Cos**的使用,它們也在symbolic包中定義。
建立一個指令碼檔案,並鍵入以下程式碼−
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)
執行檔案時,它會顯示以下結果−
ans = -45.0+x^2+(4.0)*x ans = 210.0+x^4-(43.0)*x^2+x^3+(23.0)*x ans = sin((2.0)*x) ans = cos(y+x) ans = x^(3.0)*(-7.0+x) ans = (-3.0+x)*x^(4.0)*(-5.0+x)
代數表示式的因式分解和化簡
**factor**函式對錶達式進行因式分解,**simplify**函式對錶達式進行化簡。以下示例演示了這個概念 -
示例
建立一個指令碼檔案,並鍵入以下程式碼−
syms x syms y factor(x^3 - y^3) factor([x^2-y^2,x^3+y^3]) simplify((x^4-16)/(x^2-4))
執行檔案時,它會顯示以下結果−
ans = (x - y)*(x^2 + x*y + y^2) ans = [ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)] ans = x^2 + 4
MATLAB - 微積分
MATLAB提供了多種方法來解決微積分問題,求解任意階的微分方程以及計算極限。最棒的是,你可以輕鬆地繪製複雜函式的圖形,並透過求解原始函式及其導數來檢查圖形上的最大值、最小值和其他駐點。
本章將討論微積分問題。在本章中,我們將討論預備微積分的概念,即計算函式的極限並驗證極限的性質。
在下一章“微分”中,我們將計算表示式的導數,並在圖形上找到區域性最大值和最小值。我們還將討論求解微分方程。
最後,在“積分”一章中,我們將討論積分學。
計算極限
MATLAB提供了**limit**函式用於計算極限。在其最基本的形式中,**limit**函式將表示式作為引數,並找到當自變數趨於零時表示式的極限。
例如,讓我們計算函式f(x) = (x3 + 5)/(x4 + 7)在x趨於零時的極限。
syms x limit((x^3 + 5)/(x^4 + 7))
MATLAB將執行上述語句並返回以下結果:
ans = 5/7
limit函式屬於符號計算的範疇;你需要使用**syms**函式來告訴MATLAB你正在使用哪些符號變數。你還可以計算函式的極限,當變數趨於某個非零數時。為了計算lim x->a(f(x)),我們使用帶有引數的limit命令。第一個是表示式,第二個是x接近的數字,這裡它是a。
例如,讓我們計算函式f(x) = (x-3)/(x-1)在x趨於1時的極限。
limit((x - 3)/(x-1),1)
MATLAB將執行上述語句並返回以下結果:
ans = NaN
讓我們再舉一個例子,
limit(x^2 + 5, 3)
MATLAB將執行上述語句並返回以下結果:
ans = 14
使用Octave計算極限
以下是使用**symbolic**包的上述示例的Octave版本,嘗試執行並比較結果 -
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)
Octave將執行上述語句並返回以下結果 -
ans = 0.7142857142857142857
驗證極限的基本性質
代數極限定理提供了一些極限的基本性質。它們如下 -
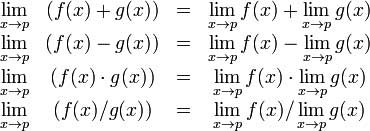
讓我們考慮兩個函式 -
- f(x) = (3x + 5)/(x - 3)
- g(x) = x2 + 1。
讓我們計算這兩個函式在x趨於5時的極限,並使用這兩個函式和MATLAB驗證極限的基本性質。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
syms x f = (3*x + 5)/(x-3); g = x^2 + 1; l1 = limit(f, 4) l2 = limit (g, 4) lAdd = limit(f + g, 4) lSub = limit(f - g, 4) lMult = limit(f*g, 4) lDiv = limit (f/g, 4)
執行檔案時,它會顯示−
l1 = 17 l2 = 17 lAdd = 34 lSub = 0 lMult = 289 lDiv = 1
使用Octave驗證極限的基本性質
以下是使用**symbolic**包的上述示例的Octave版本,嘗試執行並比較結果 -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)
Octave將執行上述語句並返回以下結果 -
l1 = 17.0 l2 = 17.0 lAdd = 34.0 lSub = 0.0 lMult = 289.0 lDiv = 1.0
左側和右側極限
當函式在變數的某個特定值處存在間斷時,該點的極限不存在。換句話說,當x從左側逼近a時的極限值不等於x從右側逼近a時的極限值時,函式f(x)在x = a處存在間斷。
這導致了左側極限和右側極限的概念。左側極限定義為x從左側趨於a時的極限,即x逼近a,且x < a。右側極限定義為x從右側趨於a時的極限,即x逼近a,且x > a。當左側極限和右側極限不相等時,極限不存在。
讓我們考慮一個函式 -
f(x) = (x - 3)/|x - 3|
我們將證明limx->3 f(x)不存在。MATLAB透過兩種方式幫助我們證實這一點 -
- 透過繪製函式的圖形並顯示間斷點。
- 透過計算極限並顯示兩者不同。
左側和右側極限是透過將字元字串'left'和'right'作為最後一個引數傳遞給limit命令來計算的。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
f = (x - 3)/abs(x-3); ezplot(f,[-1,5]) l = limit(f,x,3,'left') r = limit(f,x,3,'right')
當你執行檔案時,MATLAB將繪製以下圖形

之後將顯示以下輸出 -
l = -1 r = 1
MATLAB - 微分
MATLAB提供了**diff**命令用於計算符號導數。在其最簡單的形式中,你將要微分的函式作為引數傳遞給diff命令。
例如,讓我們計算函式f(t) = 3t2 + 2t-2的導數。
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
syms t f = 3*t^2 + 2*t^(-2); diff(f)
編譯並執行上述程式碼後,會產生以下結果:
ans = 6*t - 4/t^3
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave執行程式碼並返回以下結果 -
ans = -(4.0)*t^(-3.0)+(6.0)*t
驗證微分的基本規則
讓我們簡要說明函式微分的各種方程或規則,並驗證這些規則。為此,我們將使用f'(x)表示一階導數,f"(x)表示二階導數。
以下是微分的規則 -
規則1
對於任何函式f和g以及任何實數a和b,函式 -
**h(x) = af(x) + bg(x)**關於x的導數由 -
h'(x) = af'(x) + bg'(x)
規則2
**加法**和**減法**規則指出,如果f和g是兩個函式,f'和g'分別是它們的導數,則,
(f + g)' = f' + g'
(f - g)' = f' - g'
規則3
**乘積**規則指出,如果f和g是兩個函式,f'和g'分別是它們的導數,則,
(f.g)' = f'.g + g'.f
規則4
**商**規則指出,如果f和g是兩個函式,f'和g'分別是它們的導數,則,
(f/g)' = (f'.g - g'.f)/g2
規則5
**多項式**或基本冪規則指出,如果y = f(x) = xn,則f' = n. x(n-1)
該規則的一個直接結果是任何常數的導數為零,即如果y = k,任何常數,則
f' = 0
規則6
鏈式法則指出,函式的函式h(x) = f(g(x))關於x的導數為:
h'(x)= f'(g(x)).g'(x)
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
執行檔案後,MATLAB 顯示以下結果:
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave執行程式碼並返回以下結果 -
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
指數函式、對數函式和三角函式的導數
下表提供了常用指數函式、對數函式和三角函式的導數:
| 函式 | 導數 |
|---|---|
| ca.x | ca.x.ln c.a(ln 為自然對數) |
| ex | ex |
| ln x | 1/x |
| lncx | 1/x.ln c |
| xx | xx.(1 + ln x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | sec2(x),或 1/cos2(x),或 1 + tan2(x) |
| cot(x) | -csc2(x),或 -1/sin2(x),或 -(1 + cot2(x)) |
| sec(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
示例
建立一個指令碼檔案,並將以下程式碼輸入其中−
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
執行檔案後,MATLAB 顯示以下結果:
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave執行程式碼並返回以下結果 -
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
計算高階導數
要計算函式 f 的高階導數,我們使用語法diff(f,n)。
讓我們計算函式 y = f(x) = x .e-3x 的二階導數。
f = x*exp(-3*x); diff(f, 2)
MATLAB 執行程式碼並返回以下結果:
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave執行程式碼並返回以下結果 -
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
示例
在這個例子中,讓我們解決一個問題。給定一個函式y = f(x) = 3 sin(x) + 7 cos(5x)。我們需要找出方程f" + f = -5cos(2x)是否成立。
建立一個指令碼檔案,並將以下程式碼輸入其中−
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
執行檔案時,它會顯示以下結果−
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave執行程式碼並返回以下結果 -
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
尋找曲線的極大值和極小值
如果我們正在尋找圖形的區域性極大值和極小值,我們基本上是在尋找函式圖形在特定區域性或特定符號變數值範圍內最高或最低的點。
對於函式 y = f(x),圖形上斜率為零的點稱為駐點。換句話說,駐點是 f'(x) = 0 的點。
為了找到函式的駐點,我們需要求導,並將導數設為零並求解方程。
示例
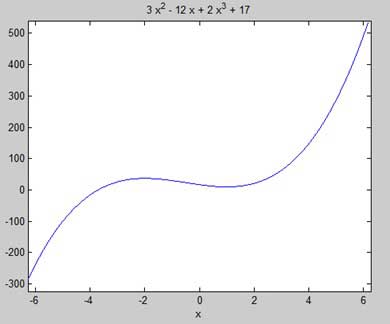
讓我們找到函式 f(x) = 2x3 + 3x2 − 12x + 17 的駐點。
採取以下步驟:
首先,讓我們輸入函式並繪製其圖形。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB 執行程式碼並返回以下圖形:
以下是上述示例的 Octave 等效程式碼:
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
我們的目標是在圖形上找到一些區域性極大值和極小值,因此讓我們在圖形的區間 [-2, 2] 上找到區域性極大值和極小值。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB 執行程式碼並返回以下圖形:
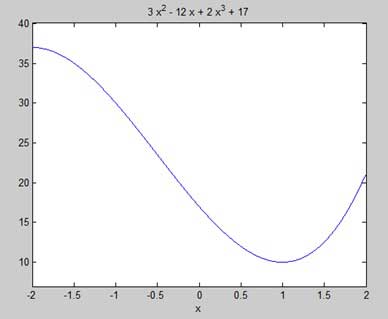
以下是上述示例的 Octave 等效程式碼:
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
接下來,讓我們計算導數。
g = diff(y)
MATLAB 執行程式碼並返回以下結果:
g = 6*x^2 + 6*x - 12
以下是上述計算的 Octave 等效程式碼:
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave執行程式碼並返回以下結果 -
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
讓我們求解導數函式 g,以獲得其變為零的值。
s = solve(g)
MATLAB 執行程式碼並返回以下結果:
s = 1 -2
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave執行程式碼並返回以下結果 -
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
這與我們的圖形一致。因此,讓我們在臨界點 x = 1, -2 處計算函式 f 的值。 我們可以使用subs命令在符號函式中替換一個值。
subs(y, 1), subs(y, -2)
MATLAB 執行程式碼並返回以下結果:
ans = 10 ans = 37
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
因此,函式 f(x) = 2x3 + 3x2 − 12x + 17 在區間 [-2,2] 上的最小值和最大值分別為 10 和 37。
求解微分方程
MATLAB 提供了dsolve命令來符號求解微分方程。
dsolve命令用於求解單個方程的最基本形式是
dsolve('eqn')
其中eqn是用於輸入方程的文字字串。
它返回一個符號解,其中包含一組 MATLAB 標記為 C1、C2 等的任意常數。
您還可以為問題指定初始條件和邊界條件,作為方程後面的逗號分隔列表,如下所示:
dsolve('eqn','cond1', 'cond2',…)
為了使用 dsolve 命令,導數用 D 表示。例如,方程 f'(t) = -2*f + cost(t) 輸入為:
'Df = -2*f + cos(t)'
高階導數用 D 後跟導數的階數表示。
例如,方程 f"(x) + 2f'(x) = 5sin3x 應輸入為:
'D2y + 2Dy = 5*sin(3*x)'
讓我們舉一個一階微分方程的簡單例子:y' = 5y。
s = dsolve('Dy = 5*y')
MATLAB 執行程式碼並返回以下結果:
s = C2*exp(5*t)
讓我們再舉一個二階微分方程的例子:y" - y = 0,y(0) = -1,y'(0) = 2。
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB 執行程式碼並返回以下結果:
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB - 積分
積分處理兩種本質上不同的問題型別。
在第一種型別中,給定函式的導數,我們想要找到該函式。因此,我們基本上是反轉微分過程。這個反向過程稱為反微分、求原函式或求不定積分。
第二類問題涉及將非常多的非常小的量加起來,然後取這些量的大小接近零時的極限,而項數趨於無窮大。這個過程導致了定積分的定義。
定積分用於求面積、體積、重心、慣性矩、力做的功以及許多其他應用。
使用 MATLAB 求不定積分
根據定義,如果函式 f(x) 的導數是 f'(x),那麼我們說 f'(x) 關於 x 的不定積分是 f(x)。例如,由於 x2 關於 x 的導數是 2x,所以我們可以說 2x 的不定積分是 x2。
用符號表示:
f'(x2) = 2x,因此,
∫ 2xdx = x2。
不定積分不是唯一的,因為對於任意常數 c 的值,x2 + c 的導數也將是 2x。
用符號表示為:
∫ 2xdx = x2 + c.
其中,c 稱為“任意常數”。
MATLAB 提供了一個int命令來計算表示式的積分。要推匯出函式不定積分的表示式,我們寫:
int(f);
例如,從我們之前的例子:
syms x int(2*x)
MATLAB 執行上述語句並返回以下結果:
ans = x^2
示例 1
在這個例子中,讓我們找到一些常用表示式的積分。建立一個指令碼檔案,並在其中鍵入以下程式碼:
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
執行檔案時,它會顯示以下結果−
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
示例 2
建立一個指令碼檔案,並在其中鍵入以下程式碼−
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
請注意,pretty函式以更易讀的格式返回表示式。
執行檔案時,它會顯示以下結果−
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
使用 MATLAB 求定積分
根據定義,定積分基本上是和的極限。我們使用定積分來求面積,例如曲線與 x 軸之間的面積以及兩條曲線之間的面積。定積分也可以用於其他情況,其中所需的數量可以表示為和的極限。
int函式可以透過傳遞要計算積分的極限來用於定積分。
計算

我們寫:
int(x, a, b)
例如,要計算 的值,我們寫:
的值,我們寫:
int(x, 4, 9)
MATLAB 執行上述語句並返回以下結果:
ans = 65/2
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave執行程式碼並返回以下結果 -
Area: 32.500
可以使用 Octave 提供的 quad() 函式給出另一種解決方案,如下所示:
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave執行程式碼並返回以下結果 -
Area: 32.500
示例 1
讓我們計算 x 軸、曲線 y = x3−2x+5 和縱座標 x = 1 和 x = 2 所包圍的面積。
所需面積由下式給出:

建立一個指令碼檔案,並鍵入以下程式碼−
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
執行檔案時,它會顯示以下結果−
a = 23/4 Area: 5.7500
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave執行程式碼並返回以下結果 -
Area: 5.7500
可以使用 Octave 提供的 quad() 函式給出另一種解決方案,如下所示:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave執行程式碼並返回以下結果 -
Area: 5.7500
示例 2
求曲線 f(x) = x2 cos(x) 在 −4 ≤ x ≤ 9 範圍內的面積。
建立一個指令碼檔案,並編寫以下程式碼:
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
執行檔案後,MATLAB 會繪製圖形:

輸出如下:
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
以下是上述計算的Octave等價物 -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB - 多項式
MATLAB 將多項式表示為包含按降冪排序的係數的行向量。例如,方程 P(x) = x4 + 7x3 - 5x + 9 可以表示為:
p = [1 7 0 -5 9];
評估多項式
polyval函式用於在指定值處評估多項式。例如,要評估我們之前在 x = 4 處的多項式p,鍵入:
p = [1 7 0 -5 9]; polyval(p,4)
MATLAB 執行上述語句並返回以下結果:
ans = 693
MATLAB 還提供了polyvalm函式來評估矩陣多項式。矩陣多項式是多項式,其變數為矩陣。
例如,讓我們建立一個方陣 X 並評估多項式 p 在 X 處的值:
p = [1 7 0 -5 9]; X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8]; polyvalm(p, X)
MATLAB 執行上述語句並返回以下結果:
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269
查詢多項式的根
roots函式計算多項式的根。例如,要計算我們多項式 p 的根,鍵入:
p = [1 7 0 -5 9]; r = roots(p)
MATLAB 執行上述語句並返回以下結果:
r = -6.8661 + 0.0000i -1.4247 + 0.0000i 0.6454 + 0.7095i 0.6454 - 0.7095i
poly函式是 roots 函式的反函式,並返回到多項式係數。例如:
p2 = poly(r)
MATLAB 執行上述語句並返回以下結果:
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000i
多項式曲線擬合
polyfit函式找到以最小二乘意義擬合一組資料的多項式的係數。如果 x 和 y 是兩個包含要擬合到 n 次多項式的 x 和 y 資料的向量,那麼我們可以透過編寫以下程式碼獲得擬合數據的多項式:
p = polyfit(x,y,n)
示例
建立一個指令碼檔案,並鍵入以下程式碼−
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data p = polyfit(x,y,4) %get the polynomial % Compute the values of the polyfit estimate over a finer range, % and plot the estimate over the real data values for comparison: x2 = 1:.1:6; y2 = polyval(p,x2); plot(x,y,'o',x2,y2) grid on
執行檔案後,MATLAB 顯示以下結果:
p = 4.1056 -47.9607 222.2598 -362.7453 191.1250
並繪製以下圖形:
MATLAB - 變換
MATLAB 提供了用於處理變換的命令,例如拉普拉斯變換和傅立葉變換。變換在科學和工程中用作簡化分析和從另一個角度檢視資料的工具。
例如,傅立葉變換允許我們將表示為時間函式的訊號轉換為頻率函式。拉普拉斯變換允許我們將微分方程轉換為代數方程。
MATLAB 提供了laplace、fourier和fft命令來處理拉普拉斯變換、傅立葉變換和快速傅立葉變換。
拉普拉斯變換
時間函式 f(t) 的拉普拉斯變換由以下積分給出:

拉普拉斯變換也表示為 f(t) 到 F(s) 的變換。您可以看到此變換或積分過程將 f(t)(符號變數 t 的函式)轉換為另一個函式 F(s),其變數為 s。
拉普拉斯變換將微分方程轉換為代數方程。要計算函式 f(t) 的拉普拉斯變換,請編寫:
laplace(f(t))
示例
在這個例子中,我們將計算一些常用函式的拉普拉斯變換。
建立一個指令碼檔案,並鍵入以下程式碼−
syms s t a b w laplace(a) laplace(t^2) laplace(t^9) laplace(exp(-b*t)) laplace(sin(w*t)) laplace(cos(w*t))
執行檔案時,它會顯示以下結果−
ans = 1/s^2 ans = 2/s^3 ans = 362880/s^10 ans = 1/(b + s) ans = w/(s^2 + w^2) ans = s/(s^2 + w^2)
拉普拉斯逆變換
MATLAB 允許我們使用ilaplace命令計算拉普拉斯逆變換。
例如:
ilaplace(1/s^3)
MATLAB 將執行上述語句並顯示結果:
ans = t^2/2
示例
建立一個指令碼檔案,並鍵入以下程式碼−
syms s t a b w ilaplace(1/s^7) ilaplace(2/(w+s)) ilaplace(s/(s^2+4)) ilaplace(exp(-b*t)) ilaplace(w/(s^2 + w^2)) ilaplace(s/(s^2 + w^2))
執行檔案時,它會顯示以下結果−
ans = t^6/720 ans = 2*exp(-t*w) ans = cos(2*t) ans = ilaplace(exp(-b*t), t, x) ans = sin(t*w) ans = cos(t*w)
傅立葉變換
傅立葉變換通常將時間數學函式 f(t) 轉換為一個新函式,有時表示為或 F,其引數為頻率,單位為週期/秒(赫茲)或弧度/秒。然後將新函式稱為傅立葉變換和/或函式 f 的頻譜。
示例
建立一個指令碼檔案,並在其中鍵入以下程式碼−
syms x f = exp(-2*x^2); %our function ezplot(f,[-2,2]) % plot of our function FT = fourier(f) % Fourier transform
執行檔案後,MATLAB 會繪製以下圖形:

顯示以下結果:
FT = (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2
繪製傅立葉變換為:
ezplot(FT)
給出以下圖形:

傅立葉逆變換
MATLAB 提供了ifourier命令來計算函式的傅立葉逆變換。例如,
f = ifourier(-2*exp(-abs(w)))
MATLAB 將執行上述語句並顯示結果:
f = -2/(pi*(x^2 + 1))
MATLAB - GNU Octave 教程
GNU Octave 是一種類似於 MATLAB 的高階程式語言,並且與 MATLAB 大部分相容。它也用於數值計算。
Octave 與 MATLAB 具有以下共同特徵:
- 矩陣是基本資料型別
- 它內建支援複數
- 它具有內建的數學函式和庫
- 它支援使用者定義的函式
GNU Octave 也是免費可再分發的軟體。您可以根據自由軟體基金會發布的 GNU 通用公共許可證 (GPL) 的條款重新分發和/或修改它。
MATLAB 與 Octave 的比較
大多數 MATLAB 程式都可以在 Octave 中執行,但一些 Octave 程式可能無法在 MATLAB 中執行,因為 Octave 允許某些 MATLAB 不支援的語法。
例如,MATLAB 僅支援單引號,但 Octave 支援單引號和雙引號來定義字串。如果您正在尋找 Octave 的教程,那麼請從頭到尾閱讀本教程,它涵蓋了 MATLAB 和 Octave。
相容示例
本教程中涵蓋的幾乎所有示例都相容 MATLAB 和 Octave。讓我們在 MATLAB 和 Octave 中嘗試以下示例,該示例在沒有任何語法更改的情況下產生相同的結果。
此示例為函式 g = xe-(x2 + y2) 建立一個 3D 表面圖。建立一個指令碼檔案並鍵入以下程式碼:
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
當你執行檔案時,MATLAB將顯示以下3D圖 -

不相容的示例
儘管 Octave 中提供了 MATLAB 的所有核心功能,但也有一些功能(例如,微積分和積分),在兩種語言中的匹配並不完全相同。本教程嘗試提供兩種型別的示例,其中它們的語法有所不同。
考慮以下示例,其中 MATLAB 和 Octave 使用不同的函式來獲取曲線的面積:f(x) = x2 cos(x),其中 -4 ≤ x ≤ 9。以下是 MATLAB 版本的程式碼:
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
執行檔案後,MATLAB 會繪製圖形:

顯示以下結果
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
但是,要在 Octave 中獲得相同曲線的面積,您必須使用 **symbolic** 包,如下所示:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB - Simulink
Simulink 是一個用於動態和嵌入式系統的模擬和基於模型的設計環境,與 MATLAB 整合在一起。Simulink 也是由 MathWorks 開發的,是一種用於建模、模擬和分析多領域動態系統的資料流圖形程式語言工具。它基本上是一個圖形化塊圖工具,具有可自定義的塊庫集。
它允許您將 MATLAB 演算法整合到模型中,並將模擬結果匯出到 MATLAB 以進行進一步分析。
Simulink 支援:
- 系統級設計
- 模擬
- 自動程式碼生成
- 嵌入式系統的測試和驗證
MathWorks 提供了許多其他附加產品,以及可與 Simulink 一起使用的第三方硬體和軟體產品。
以下列表簡要介紹了其中一些:
**Stateflow** 允許開發狀態機和流程圖。
**Simulink Coder** 允許自動生成 C 原始碼,以便即時實現系統。
**xPC Target** 以及 **基於 x86 的即時系統** 提供了一個環境,可以在物理系統上即時模擬和測試 Simulink 和 Stateflow 模型。
**Embedded Coder** 支援特定的嵌入式目標。
**HDL Coder** 允許自動生成可綜合的 VHDL 和 Verilog。
**SimEvents** 提供了一個圖形化構建塊庫,用於建模排隊系統。
Simulink 能夠透過建模風格檢查、需求跟蹤和模型覆蓋率分析來系統地驗證和確認模型。
Simulink Design Verifier 允許您識別設計錯誤併為模型檢查生成測試用例場景。
使用 Simulink
要開啟 Simulink,請在 MATLAB 工作空間中鍵入:
simulink
Simulink 將開啟 **庫瀏覽器**。庫瀏覽器用於構建模擬模型。

在左側視窗窗格中,您會發現幾個根據各種系統分類的庫,單擊每個庫將在右側視窗窗格中顯示設計塊。
構建模型
要建立新模型,請單擊庫瀏覽器工具欄上的 **新建** 按鈕。這將開啟一個新的無標題模型視窗。
Simulink 模型是一個塊圖。
模型元素是透過從庫瀏覽器中選擇相應的元素並將其拖放到模型視窗中來新增的。
或者,您可以複製模型元素並將其貼上到模型視窗中。
示例
從 Simulink 庫中拖放專案以建立您的專案。
出於本示例的目的,將使用兩個塊進行模擬 - **源**(訊號)和 **匯點**(示波器)。訊號發生器(源)生成模擬訊號,然後示波器(匯點)將以圖形方式顯示該訊號。
首先將所需的塊從庫拖到專案視窗。然後,將塊連線在一起,這可以透過將聯結器從一個塊上的連線點拖到另一個塊上的連線點來完成。
讓我們將一個“正弦波”塊拖到模型中。
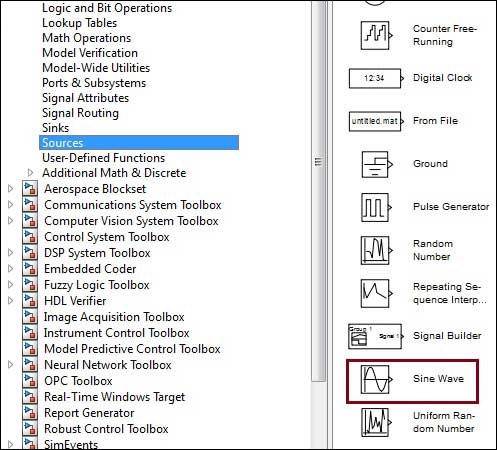
從庫中選擇“匯點”,並將“示波器”塊拖到模型中。
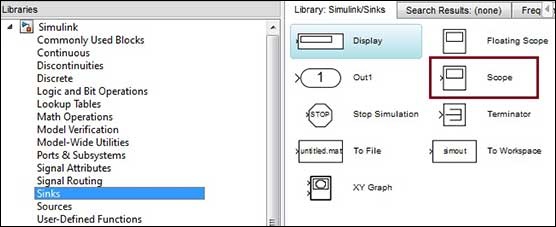
將訊號線從正弦波塊的輸出拖到示波器塊的輸入。
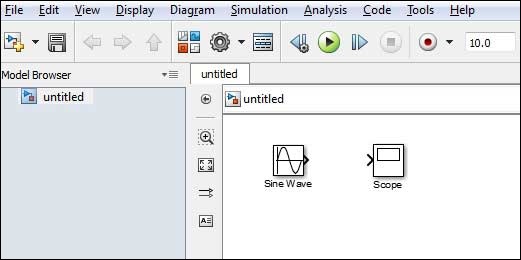

透過按下“**執行**”按鈕執行模擬,保持所有引數為預設值(您可以從“模擬”選單中更改它們)
您應該從示波器中獲得以下圖形。