MATLAB - 繪製 3D 等高線圖

等高線是在曲面或資料集中連線等值點的曲線。在資料視覺化的背景下，等高線用於表示二元函式的變化。這些線連線具有相同函式值的點，形成曲線，突出顯示強度或高度相似的區域。

對於 3D 等高線圖，這些曲線存在於三維曲面上。等高線表示曲面與平行於 XY 平面的平面的交點，它們的模式傳達了有關曲面形狀和特徵的資訊。

在 MATLAB 中建立 3D 等高線圖可以成為視覺化三維資料的強大方法。3D 等高線圖是三維曲面的圖形表示，它使用等高線來顯示資料變化。在 MATLAB 中，您可以建立此類圖來視覺化二元函式。這種型別的圖有助於理解三維空間中曲面的結構和行為。

在 matlab 中，我們有以下方法可以幫助繪製等高線，它們是：

contour3
surfc

讓我們詳細瞭解這兩種方法。

使用 contour3

MATLAB 中的 contour3 方法用於建立三維等高線圖。此函式允許您視覺化三維曲面的等高線，顯示連線具有相同函式值的點的曲線。

語法

contour3(Z)
contour3(X,Y,Z)
contour3(___,levels)
contour3(___,LineSpec)

語法的詳細解釋如下：

contour3(Z) - 生成三維等高線圖，說明從矩陣 Z 派生的等值線。Z 表示 x-y 平面上的高度值。

contour3(X,Y,Z) - 它提供了 Z 中值的 x 和 y 座標。

contour3(___,levels) - 如果將 levels 設定為標量，用 n 表示，則該函式會自動在 n 個適當選擇的級別或高度上顯示等高線。或者，如果您希望在特定高度繪製等高線，則可以將 levels 指定為具有單調遞增值的向量。對於高度為 k 的等高線，請使用一個包含兩個元素的行向量 [k k] 作為 levels 引數。

contour3(___,LineSpec) - 使用此方法，您可以更改等高線的樣式和顏色。

讓我們看看上面每個語法的一些示例。

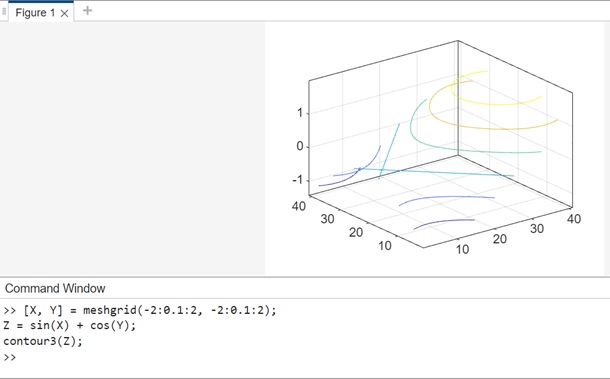
示例 1：使用 contour3(Z)

上面語法的程式碼如下：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = sin(X) + cos(Y);
contour3(Z);

在此示例中：

meshgrid 用於建立 X 和 Y 值的網格。
函式 Z = sin(X) + cos(Y) 生成一個矩陣 Z，表示 x-y 平面上的高度值。

使用 contour3(Z)，它建立了一個三維等高線圖。該函式會根據矩陣 Z 中的值自動確定要顯示的等高線。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

示例 2：使用 contour3(X,Y,Z)

上面語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = sin(X) + cos(Y);
contour3(X, Y, Z);

在此示例中：

meshgrid 用於建立 X 和 Y 值的網格。
函式 Z = sin(X) + cos(Y) 生成一個矩陣 Z，表示 x-y 平面上的高度值。

函式 contour3(X, Y, Z) 用於建立三維等高線圖。X 和 Y 矩陣提供了 Z 中值的座標。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

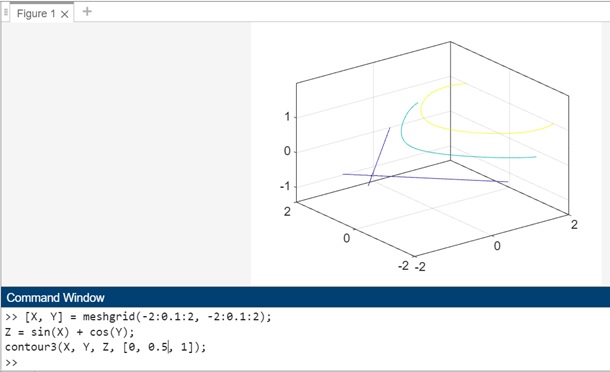
示例 3：使用 contour3(___,levels)

上面語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = sin(X) + cos(Y);
contour3(X, Y, Z, [0, 0.5, 1]);

在此示例中：

meshgrid 用於建立 X 和 Y 值的網格。
函式 Z = sin(X) + cos(Y) 生成一個矩陣 Z，表示 x-y 平面上的高度值。

函式 contour3(X, Y, Z, [0, 0.5, 1]) 用於建立三維等高線圖。向量 [0, 0.5, 1] 指定特定等高線級別。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

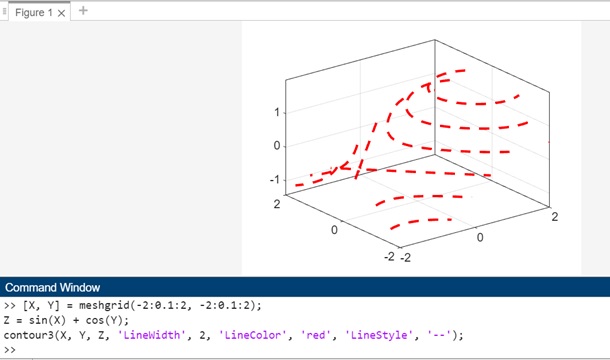
示例 4：contour3(___,LineSpec)

上面語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = sin(X) + cos(Y);
contour3(X, Y, Z, 'LineWidth', 2, 'LineColor', 'red', 'LineStyle', '--');

在此示例中：

meshgrid 用於建立 X 和 Y 值的網格。
函式 Z = sin(X) + cos(Y) 生成一個矩陣 Z，表示 x-y 平面上的高度值。

方法 contour3(X, Y, Z, 'LineWidth', 2, 'LineColor', 'red', 'LineStyle', '--') 用於建立具有自定義線型和顏色的三維等高線圖。

選項 'LineWidth', 2 指定 2 個點的線寬。
選項 'LineColor', 'red' 指定等高線的紅色。
選項 'LineStyle', '--' 指定虛線樣式。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

使用 surfc()

MATLAB 中的 surfc() 函式用於建立 3D 曲面圖，並在曲面上顯示等高線。它將曲面圖的視覺化與等高線相結合，提供了對基礎資料的全面檢視。“surfc”代表“帶等高線的曲面”。

語法

surfc(X,Y,Z)
surfc(X,Y,Z,C)
surfc(___,Name,Value)

以下是上面提到的語法的詳細解釋：

surfc(X,Y,Z) - 函式生成一個 3D 曲面圖，其中包含底層的等高線圖。在此視覺化中，曲面表示具有獨特的實體邊緣和麵顏色的三維結構。繪製的曲面基於矩陣 Z 中的值，這些值被解釋為 X 和 Y 定義的 x-y 平面中網格上方的高度。曲面的顏色根據 Z 矩陣中指定的高度而變化。

surfc(X,Y,Z,C) - 提供對生成圖中曲面顏色的顯式控制。

surfc(___,Name,Value) - 允許透過一個或多個名稱-值對引數指定曲面屬性。

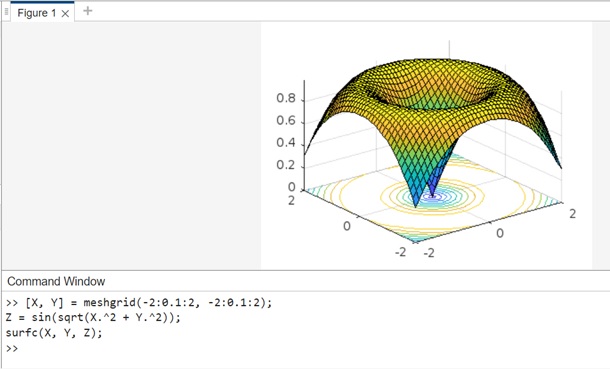
示例 1：使用 surfc(X,Y,Z)

語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = sin(sqrt(X.^2 + Y.^2));
surfc(X, Y, Z);

在此示例中：

meshgrid 用於在 x-y 平面上建立網格。
函式 sin(sqrt(X.^2 + Y.^2)) 用於根據 X 和 Y 定義曲面高度。
然後使用 surfc() 函式根據指定的 X、Y 和 Z 值建立 3D 曲面圖，並帶有底層的等高線圖。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

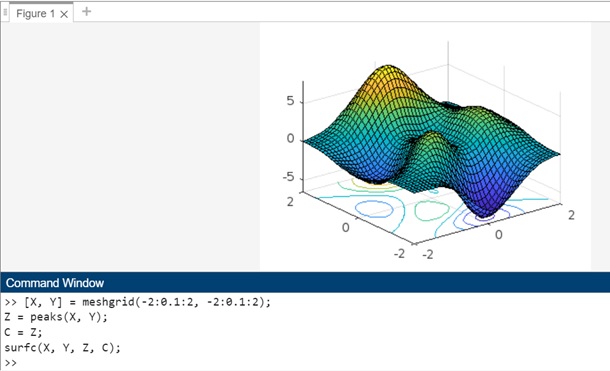
示例 2：使用 surfc(X,Y,Z,C)

上面語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = peaks(X, Y);
C = Z;
surfc(X, Y, Z, C);

在此示例中：

peaks 函式用於生成由 X 和 Y 定義的樣本曲面。
矩陣 C 被設定為等於 Z 值，這表示曲面圖中每個點的顏色值由 Z 矩陣中相應的的高度決定。
然後使用 surfc() 函式建立具有顯式表面顏色控制的 3D 曲面圖。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

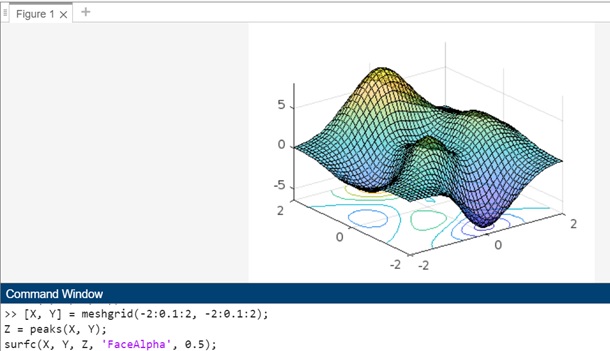
示例 3：使用語法 surfc(___,Name,Value)

上面語法的程式碼為：

[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = peaks(X, Y);
surfc(X, Y, Z, 'FaceAlpha', 0.5);

在此示例中：

使用 meshgrid 定義 x-y 平面上的網格。
peaks 函式用於生成由 X 和 Y 定義的樣本曲面。
將 'FaceAlpha', 0.5 名值對引數與 surfc() 一起使用，以將表面的透明度設定為 0.5，使其半透明。

當您在 matlab 命令視窗中執行程式碼時，輸出為：

列印頁面