MATLAB - 微積分

MATLAB 提供多種方法來解決微積分問題，求解任意階次的微分方程以及計算極限。最重要的是，您可以輕鬆繪製複雜函式的圖形，並透過求解原函式及其導數來檢查圖形上的最大值、最小值和其他靜止點。

本章將討論微積分問題。本章將討論預備微積分概念，即計算函式極限和驗證極限的性質。

在下一章微分中，我們將計算表示式的導數，並在圖形上找到區域性最大值和最小值。我們還將討論求解微分方程。

最後，在積分章節中，我們將討論積分學。

計算極限

MATLAB 提供了limit函式用於計算極限。在其最基本的形式中，limit函式將表示式作為引數，並找到當自變數趨於零時表示式的極限。

例如，讓我們計算函式 f(x) = (x³ + 5)/(x⁴ + 7) 在 x 趨於零時的極限。

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB 將執行上述語句並返回以下結果：

ans =
   5/7

limit 函式屬於符號計算的範疇；您需要使用syms函式來告訴 MATLAB 您正在使用哪些符號變數。您還可以計算函式的極限，當變數趨於某個非零數時。要計算 lim _x->a(f(x))，我們使用 limit 命令及其引數。第一個是表示式，第二個是 x 趨近的數字，這裡它是 a。

例如，讓我們計算函式 f(x) = (x-3)/(x-1) 在 x 趨於 1 時的極限。

limit((x - 3)/(x-1),1)

MATLAB 將執行上述語句並返回以下結果：

ans =
   NaN

讓我們來看另一個例子：

limit(x^2 + 5, 3)

MATLAB 將執行上述語句並返回以下結果：

ans =
   14

使用 Octave 計算極限

以下是使用symbolic包的上述示例的 Octave 版本，嘗試執行並比較結果：

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave 將執行上述語句並返回以下結果：

ans =
   0.7142857142857142857

驗證極限的基本性質

代數極限定理提供了一些極限的基本性質。這些性質如下：

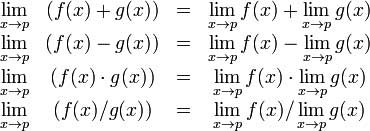
讓我們考慮兩個函式：

f(x) = (3x + 5)/(x - 3)
g(x) = x² + 1。

讓我們計算這兩個函式在 x 趨於 5 時的極限，並使用這兩個函式和 MATLAB 驗證極限的基本性質。

示例

建立一個指令碼檔案，並將以下程式碼輸入其中：

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

執行該檔案時，它將顯示：

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

使用 Octave 驗證極限的基本性質

以下是使用symbolic包的上述示例的 Octave 版本，嘗試執行並比較結果：

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave 將執行上述語句並返回以下結果：

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

左側和右側極限

當函式在變數的某個特定值處有不連續性時，該點的極限不存在。換句話說，當 x 從左側逼近 a 時極限的值不等於 x 從右側逼近 a 時極限的值時，函式 f(x) 在 x = a 處具有不連續性。

這導致了左極限和右極限的概念。左極限定義為 x 從左側趨於 a 的極限，即 x 對於 x < a 的值逼近 a。右極限定義為 x 從右側趨於 a 的極限，即 x 對於 x > a 的值逼近 a。當左極限和右極限不相等時，極限不存在。

讓我們考慮一個函式：

f(x) = (x - 3)/|x - 3|

我們將證明 lim_x->3 f(x) 不存在。MATLAB 透過兩種方式幫助我們確定這一事實：

透過繪製函式圖形並顯示不連續性。
透過計算極限並顯示兩者不同。

左極限和右極限是透過將字元字串“left”和“right”作為最後一個引數傳遞給 limit 命令來計算的。

示例

建立一個指令碼檔案，並將以下程式碼輸入其中：

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

執行該檔案時，MATLAB 將繪製以下圖形

之後將顯示以下輸出：

l =
   -1
  
r =
   1

列印頁面