網路拓撲矩陣

---

---

在上一章中，我們討論瞭如何將電路轉換為等效圖。現在，讓我們討論一下網路拓撲矩陣，它可以利用等效圖來解決任何電路或網路問題。

與網路圖相關的矩陣

以下是圖論中使用的三個矩陣。

• 關聯矩陣
• 基本回路矩陣
• 基本割集矩陣

關聯矩陣

關聯矩陣表示給定電路或網路的圖。因此，可以從**關聯矩陣**繪製出相同電路或網路的圖。

我們知道圖由一組節點組成，這些節點透過一些支路連線。因此，支路與節點的連線稱為關聯。關聯矩陣用字母A表示。它也稱為節點到支路的關聯矩陣或**節點關聯矩陣**。

如果一個**有向圖**中有'n'個節點和'b'個支路，則關聯矩陣將有'n'行和'b'列。這裡，行和列分別對應於有向圖的節點和支路。因此，關聯矩陣的**階數**將為**n × b**。

**關聯矩陣的元素**將具有以下三個值之一：+1、-1和0。

• 如果支路電流離開選定的節點，則元素的值將為+1。

• 如果支路電流進入選定的節點，則元素的值將為-1。

• 如果支路電流既不進入選定的節點，也不離開選定的節點，則元素的值將為0。

求關聯矩陣的步驟

按照以下步驟查詢有向圖的關聯矩陣。

• 一次選擇給定有向圖中的一個節點，並在該節點對應的那一行中填充關聯矩陣元素的值。

• 對給定有向圖的所有節點重複上述步驟。

示例

考慮以下**有向圖**。

對應於上述有向圖的**關聯矩陣**將是

$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$

上述矩陣的行和列分別表示給定有向圖的節點和支路。這個關聯矩陣的階數是4 × 6。

透過觀察上述關聯矩陣，我們可以得出結論：關聯矩陣的列元素的**總和**等於零。這意味著支路電流只從一個節點離開並進入另一個節點。

**注意** - 如果給定的圖是無向圖，則透過在每條支路上表示箭頭將其轉換為有向圖。我們可以考慮每條支路中電流流動的任意方向。

基本回路矩陣

基本回路或**f-迴路**是一個迴路，它只包含一個支路和一個或多個樹枝。因此，f-迴路的數量將等於支路的數量。基本回路矩陣用字母B表示。它也稱為**基本回路矩陣**和關聯矩陣。該矩陣給出支路電流和支路電流之間的關係。

如果一個**有向圖**中有'n'個節點和'b'個支路，則對應於給定圖的選定樹的餘樹中存在的支路數將為b-n+1。

因此，基本回路矩陣將有'b-n+1'行和'b'列。這裡，行和列分別對應於餘樹的支路和給定圖的支路。因此，基本回路矩陣的階數將為**(b - n + 1) × b**。

**基本回路矩陣的元素**將具有以下三個值之一：+1、-1和0。

• 對於選定f-迴路的支路，元素的值將為+1。

• 對於其餘不是選定f-迴路一部分的支路和樹枝，元素的值將為0。

• 如果選定f-迴路的樹枝電流方向與f-迴路支路電流方向相同，則元素的值將為+1。

• 如果選定f-迴路的樹枝電流方向與f-迴路支路電流方向相反，則元素的值將為-1。

求基本回路矩陣的步驟

按照以下步驟查詢給定有向圖的基本回路矩陣。

• 選擇給定有向圖的一棵樹。

• 透過一次包含一個支路，我們將得到一個f-迴路。在基本回路矩陣的一行中填充對應於此f-迴路的元素值。

• 對所有支路重複上述步驟。

示例

看一下以下**有向圖**的樹，該樹用於關聯矩陣。

上述樹包含三個支路d、e和f。因此，支路a、b和c將是對應於上述樹的餘樹的支路。透過將一個支路一次新增到上述樹中，我們將得到一個**f-迴路**。因此，由於有三個支路，將會有三個**f-迴路**。這三個f-迴路如下圖所示。

在上圖中，用彩色線表示的支路形成f-迴路。我們將從每個f-迴路獲得關聯矩陣的行元素值。因此，上述所考慮樹的**關聯矩陣**將是

$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$

上述矩陣的行和列分別表示給定有向圖的支路和支路。這個關聯矩陣的階數是3 × 6。

有向圖的**基本回路矩陣的數量**將等於該有向圖的樹的數量。因為每棵樹都將有一個基本回路矩陣。

基本割集矩陣

基本割集或**f-割集**是從圖中移除的最小數量的支路，以使原始圖變為兩個隔離的子圖。f-割集只包含**一個樹枝**和一個或多個支路。因此，f-割集的數量將等於樹枝的數量。

**基本割集矩陣**用字母C表示。該矩陣給出支路電壓和樹枝電壓之間的關係。

如果一個**有向圖**中有'n'個節點和'b'個支路，則給定圖的選定樹中存在的樹枝數將為n-1。因此，基本割集矩陣將有'n-1'行和'b'列。這裡，行和列分別對應於選定樹的樹枝和給定圖的支路。因此，基本割集矩陣的**階數**將為**(n-1) × b**。

**基本割集矩陣的元素**將具有以下三個值之一：+1、-1和0。

• 對於選定f-割集的樹枝，元素的值將為+1。

• 對於其餘不是選定f-割集一部分的樹枝和支路，元素的值將為0。

• 如果選定f-割集的支路電流方向與f-割集樹枝電流方向相同，則元素的值將為+1。

• 如果選定f-割集的支路電流方向與f-割集樹枝電流方向相反，則元素的值將為-1。

求基本割集矩陣的步驟

按照以下步驟查詢給定有向圖的基本割集矩陣。

• 選擇給定有向圖的一棵樹，並用虛線表示支路。

• 透過一次移除一個樹枝和必要的支路，我們將得到一個f-割集。在基本割集矩陣的一行中填充對應於此f-割集的元素值。

• 對所有樹枝重複上述步驟。

示例

考慮我們在關聯矩陣部分中討論的相同的**有向圖**。選擇該有向圖的支路d、e和f作為樹枝。因此，該有向圖的其餘支路a、b和c將是支路。

**樹枝**d、e和f用實線表示，**支路**a、b和c在下圖中用虛線表示。

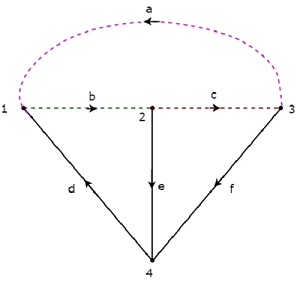
透過一次移除一個樹枝和必要的支路，我們將得到一個f-割集。因此，由於有三個樹枝，將會有三個f-割集。這三個**f-割集**如下圖所示。

透過移除C₁、C₂和C₃的一組樹枝和支路，我們將有三個f-割集。我們將從每個f-割集獲得基本割集矩陣的行元素值。因此，上述所考慮樹的**基本割集矩陣**將是

$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$

上述矩陣的行和列分別表示給定有向圖的樹枝和支路。這個基本割集矩陣的階數是3 × 6。

有向圖的**基本割集矩陣的數量**將等於該有向圖的樹的數量。因為每棵樹都將有一個基本割集矩陣。