Network Theory

網路理論教程

網路理論教程

網路理論，也稱為電路理論，是電氣和電子工程學科的基本學科之一。網路理論提供了電量的基本定義、定律和分析電路的方法。您可以使用本教程作為指南來學習網路理論或電路理論的原理。

本教程涵蓋了諸如電荷、電流、電壓、電動勢、歐姆定律、基爾霍夫定律、諾頓定理、戴維南定理、節點和網孔分析、交流電路、三相電路、電力、二埠網路等主題。

Network Theory Tutorial

電路理論知識對於設計、分析和排除各種電路和系統的故障至關重要。本教程提供了電路的理論和實踐知識。對於希望瞭解學習電氣和電子工程所需的基本概念的學生來說，本教程可以被認為是非常有用的資源。

電路理論導論

電路理論是電氣和電子工程中最基本的學科，它涉及電氣電路和網路的設計、分析和研究。它也被稱為網路理論、網路分析、電路分析、電路基礎等。

電路理論提供了合成和分析各種應用（如電機、電力電子、電力系統、通訊系統、訊號處理等）的電氣電路所需的定律、原理和方法。

什麼是電氣網路？

在電氣工程中，網路只不過是電氣元件（如電阻、電感、電容、導線、電池等）的互連佈置。

如果一個電氣網路具有能量源並且有一個電流流動的閉合路徑，則稱為電路。

下圖描繪了一個典型的電氣網路和一個電路：

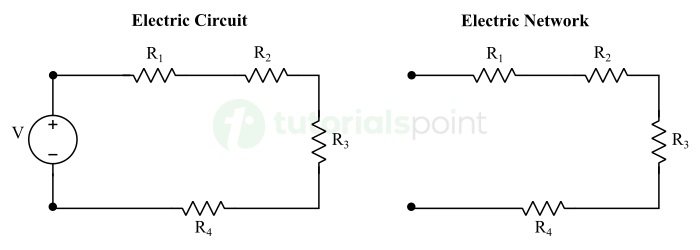
What is a Network in Electrical?

什麼是網路分析？

網路分析或電路分析是確定電路中電激發或響應的過程。

換句話說，網路分析是確定電路中各個元件上的電壓和流過它們的電流的過程。

在電路理論中，有幾種可用於分析電路的定律和方法，例如歐姆定律、KCL、KVL、戴維南定理、諾頓定理、疊加定理等。

網路理論中的重要定義

以下是一些在網路理論中起著至關重要作用的關鍵定義：

電路元件

具有兩個或多個端子的電氣裝置，並允許電流流過，稱為電路元件。它也稱為電路元素。

節點

在電路中，兩個或多個元件連線在一起的點稱為節點。具有接地電位的節點被認為是電路中的參考節點，它用於電路分析的目的。

結點

電路中三個或多個元件連線在一起的節點稱為結點。

支路

電路中兩個結點之間的部分稱為支路。

迴路和網孔

電氣元件的閉合路徑稱為迴路。網孔是一個基本回路，它不包含任何其他迴路。

埠

電路的輸入和輸出端子稱為埠。例如，電池的兩個端子是其輸出埠。

傳遞函式

傳遞函式是一個數學表示式，表示電路的輸入和輸出之間的關係。

元件傳遞函式

對於只有兩個端子（即單埠元件）的電路，傳遞函式以阻抗或導納為單位計算，稱為元件傳遞函式。

等效電路

複雜電路或網路的簡化版本，具有相同的輸入和輸出，稱為等效電路。如果兩個電路在同一對端子之間具有相同的電壓和電流關係，則稱這兩個電路彼此等效。

電阻電路

僅具有電阻作為能量消耗元件和電流或電壓源作為能量供應元件的電路稱為電阻電路。

為什麼電路理論很重要？

電路理論是電氣和電子工程領域的重要學科，原因如下：

  • 它提供了輕鬆分析電路的定律、原理和方法。
  • 它允許工程師設計和合成我們日常生活中使用的裝置和系統的電路。
  • 它還提供了電路分析工具，使它們更加可靠和高效。
  • 它為理解電力系統、電力電子、類比電子、電機和驅動等電氣工程中的複雜概念奠定了基礎。
  • 它提供了故障排除和最佳化電氣系統的工具。

電路理論的優缺點

電路理論提供了一個處理各種電路和系統的科學框架。但是，它既有優點也有侷限性，在下表中突出顯示：

電路理論的優點 電路理論的缺點
電路理論提供了關於電路定律、定理和原理的全面知識。 電路理論主要假設電路元件（如R、L、C等）是集總的和線性的。在處理分散式和非線性元件時，它有一些侷限性。
電路理論提供了各種有效的方法將複雜電路簡化為更簡單的版本。 對於非線性電路，電路分析理論變得更加複雜，需要其他方法。
電路理論具有廣泛的應用，從基礎物理學到現代電力系統和機器人技術。 在電磁場占主導地位的地方（如天線設計）電路理論變得無效。
電路理論提供了交流 (AC) 和直流 (DC) 電路的分析技術。 電路理論中的許多概念都是基於理想假設，並在實際應用中引入了缺陷。
電路理論還提供了一些工具和技術來設計和合成高效的電路和系統。 電路理論有時無法模擬某些特定型別的功率損耗和噪聲，如介質損耗、輻射損耗等。

電路理論的應用

電路理論是整個電氣和電子工程的支柱，它具有廣泛的應用。下面列出了電路理論在各個領域的某些主要應用：

  • 電力系統 - 電力系統中的電路理論有助於設計和實施可靠高效的電力傳輸和分配電網。
  • 電子學 - 電路理論在模擬和數位電子學中發揮著至關重要的作用，因為它允許設計高效的電子電路，如放大器、整流器、削波器、濾波器、振盪器等。
  • 訊號與系統 - 電路理論也可用於訊號與系統中分析和處理訊號。
  • 消費電子產品 - 電路理論用於設計計算機、筆記型電腦、手機、電視等電子裝置的電路。它也用於分析和排除這些裝置的故障。
  • 通訊系統 - 電路理論有助於開發通訊系統中使用的放大器、發射機、接收機、濾波器等電路。

這些電路理論應用示例證明了它在電氣和電子工程領域的通用性。

您將在網路理論教程中學習什麼？

本網路理論綜合教程涵蓋了大量重要主題，這些主題是發展電路基礎和掌握電氣和電子工程中其他高階概念所必需的。下表給出了本教程中涵蓋的每個章節的基本概述：

章節 描述
網路理論概述 本章介紹了網路理論中的基本概念，如電路和網路的概念、基本電量、電路元件的型別等。
網路理論中的有源元件 在本章中，您將瞭解什麼是電路中的有源元件？您還將學習獨立源和受控源。
網路理論中的無源元件 在本節中，我們將詳細討論電路中的三個關鍵無源元件，即電阻、電感和電容。
基爾霍夫定律 本章解釋了網路理論中兩個最基本的定律，即KCL（基爾霍夫電流定律）和KVL（基爾霍夫電壓定律）。
電量分配原理 在本節中，您將學習電路的兩個原理，即電壓分配規則和電流分配規則。
節點分析 本節詳細解釋瞭如何使用節點分析方法求解電路。
網孔分析 在本章中，您將瞭解使用網孔分析方法求解電路的過程和應用。
等效電路 本章演示了將複雜的串聯和並聯電路簡化到其最簡單形式的方法。
三角形到星形轉換 本章解釋了將三角形網路表示為其等效星形網路的過程。
星形到三角形轉換 本節演示了將星形網路轉換為其等效三角形網路的過程。
網路拓撲 在本章中，您將學習網路拓撲（圖論）的概念、圖論的基本術語以及不同型別的網路圖。
網路拓撲矩陣 本章討論了網路拓撲矩陣，這些矩陣可用於透過使用其等效圖來解決任何電路或網路問題。
疊加定理 在本章中，您將找到關於使用疊加定理求解電路的詳細解釋。
戴維南定理 本章提供了關於戴維南定理求解電路的分步說明。
諾頓定理 本章透過求解示例解釋了使用諾頓定理求解電路的方法。
最大功率傳輸定理 本章描述了最大功率傳輸定理的陳述，以及最大功率傳輸的條件和最大功率傳輸時的效率。
直流電路響應 在本章中，您將瞭解直流電路的暫態和穩態響應，並將學習如何找到串聯RL電路的響應。
交流電路響應 本章描述了求解串聯RL電路交流響應的過程。
串聯諧振 本章定義了諧振，並提供了對串聯諧振電路的研究。
並聯諧振 在本章中，您將學習並聯諧振電路中的電路圖和電氣量。
耦合電路 本節概述了耦合電路和電路中耦合的型別。
二埠網路 本章描述了二埠網路和不同型別的二埠網路引數。
二埠引數轉換 在本章中，您將學習轉換二埠網路引數的過程。
濾波器 本節描述了電路中不同型別的濾波器。

網路理論常見問題解答

在本節中，我們收集了一些關於網路理論的常見問題解答 (FAQ)，以及它們的答案。

在電氣工程中，網路理論是一門核心學科，它使用數學原理研究電路，以確定其行為。它有助於分析包含電阻、電容、電感和電源的電路。
疊加定理是用於分析包含多個獨立電源的電路的基本定理。在此定理中，分別確定電路對每個獨立電源的響應，並透過將每個電源的響應相加來確定電路的最終響應。
基爾霍夫提出了兩個用於電路分析的基本定律，稱為基爾霍夫電流定律 (KCL) 和基爾霍夫電壓定律 (KVL)。KCL 提供了一種計算電路中節點進入和離開的總電流的方法，而 KVL 說明了在閉合路徑周圍查詢總電壓的方法。
節點分析和網孔分析的主要區別在於，節點分析基於KCL（基爾霍夫電流定律），而網孔分析基於KVL（基爾霍夫電壓定律）。
戴維南定理和諾頓定理都可將複雜的線性電網路簡化為最簡單的形式以進行分析。其中，戴維南定理將複雜電路簡化為一個等效的簡化電路，該電路包含一個電壓源和一個與之串聯的電阻。另一方面，諾頓定理將複雜電路簡化為一個等效的簡化電路，該電路包含一個電流源和一個與之並聯的電阻。

在串聯電路中，如果連線了N個電阻，則串聯電路的總電阻使用以下關係式計算：

$$\mathrm{R_t = R_1 + R_2 + R_3 + \dots + R_N}$$

類似地，在由N個電阻組成的並聯電路中，總電阻使用以下表達式計算：

$$\mathrm{\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_N}}$$

並聯電路中有一種特殊情況，當只有兩個電阻並聯連線時，總電阻計算如下：

$$\mathrm{R_t = \frac{R_1 R_2}{R_1 + R_2}}$$

在RLC電路中，諧振是在特定頻率（稱為諧振頻率）下發生的一種狀態，在此頻率下，感抗與容抗大小相等且方向相反，從而相互抵消。在諧振條件下，RLC電路表現為純電阻電路。
拉普拉斯變換 (LT) 是一種數學技術，用於在電路分析中將時域微分方程轉換為s域中的簡單代數方程。它主要用於分析包含電容器和電感的電路的暫態行為。

電容器和電感器在交流和直流電路中的行為如下：

  • 在直流電路中，電容器在充電後阻斷直流電流，而電感器允許直流電流透過。
  • 在交流電路中，電容器允許交流電流透過，而電感器試圖阻斷交流電流的變化。

有時在處理電路時，我們會發現一些連線既不是串聯也不是並聯。相反，它們以三角形 (Δ) 或星形 (Y) 配置連線。

為了簡化包含三角形 (Δ) 和星形 (Y) 連線的電路的分析，我們需要將三角形轉換為星形或星形轉換為三角形。這些方法被稱為三角形-星形變換和星形-三角形變換。

列印頁面
上一頁
下一頁
廣告