網路理論 - 節點分析

---

---

解決任何電網路有兩種基本方法：節點分析和網孔分析。在本章中，讓我們討論節點分析方法。

在節點分析中，我們將考慮相對於地面的節點電壓。因此，節點分析也稱為節點電壓法。

節點分析步驟

使用節點分析法解決任何電網路或電路時，請遵循以下步驟。

• 步驟 1 - 識別主節點並選擇其中一個作為參考節點。我們將把該參考節點視為接地。

• 步驟 2 - 從所有主節點（除參考節點外）相對於地標記節點電壓。

• 步驟 3 - 在所有主節點（除參考節點外）處編寫節點方程。節點方程是首先應用KCL，然後應用歐姆定律得到的。

• 步驟 4 - 求解步驟 3 中獲得的節點方程，以獲得節點電壓。

現在，我們可以使用節點電壓找到流過任何元件的電流以及任何存在於給定網路中的元件兩端的電壓。

示例

使用節點分析法求解以下電路中 20 Ω 電阻的電流。

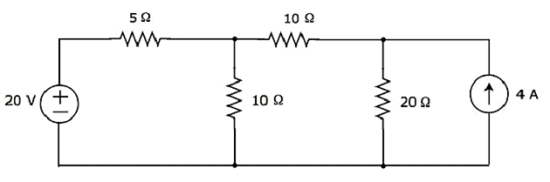
步驟 1 - 上述電路中有三個主節點。它們在以下圖中標記為 1、2 和 3。

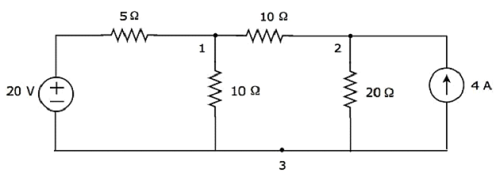
在上圖中，將節點 3視為參考節點（接地）。

步驟 2 - 節點電壓 V₁ 和 V₂ 在下圖中標記。

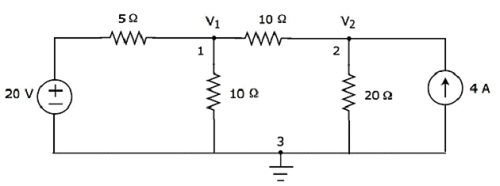
在上圖中，V₁ 是節點 1 相對於地面的電壓，V₂ 是節點 2 相對於地面的電壓。

步驟 3 - 在這種情況下，我們將得到兩個節點方程，因為除了接地之外還有兩個主節點 1 和 2。當我們在節點處編寫節點方程時，假設所有電流都從未指定電流方向的節點發出，並且該節點的電壓大於電路中的其他節點電壓。

節點 1 的節點方程為

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$

$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$

$$\Rightarrow 4V_1 - 40 - V_2 = 0$$

$\Rightarrow V_2 = 4V_1 - 40$ 方程 1

節點 2 的節點方程為

$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$

$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$

$\Rightarrow 3V_2 − 2V_1 = 80$ 方程 2

步驟 4 - 透過求解方程 1 和方程 2 求解節點電壓 V₁ 和 V₂。

將方程 1 代入方程 2。

$$3(4 V_1 - 40) - 2 V_1 = 80$$

$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$

$$\Rightarrow 10 V_1 = 200$$

$$\Rightarrow V_1 = 20V$$

將 V₁ = 20 V 代入方程 1。

$$V_2 = 4(20) - 40$$

$$\Rightarrow V_2 = 40V$$

因此，我們得到了節點電壓 V₁ 和 V₂ 分別為20 V和40 V。

步驟 5 - 20 Ω 電阻兩端的電壓就是節點電壓 V₂，等於 40 V。現在，我們可以使用歐姆定律求解流過 20 Ω 電阻的電流。

$$I_{20 \Omega} = \frac{V_2}{R}$$

將 V₂ 和 R 的值代入上述方程。

$$I_{20 \Omega} = \frac{40}{20}$$

$$\Rightarrow I_{20 \Omega} = 2A$$

因此，給定電路中 20 Ω 電阻的電流為2 A。

注意 - 從上面的例子中，我們可以得出結論，如果電路有 'n' 個主節點（參考節點除外），那麼我們必須求解 'n' 個節點方程。因此，當主節點數（參考節點除外）小於任何電路的網孔數時，我們可以選擇節點分析。