網路理論 - 無源元件

---

---

本章將詳細討論無源元件，例如電阻器、電感器和電容器。讓我們從電阻器開始。

電阻器

電阻器主要功能是阻礙或限制電流的流動。因此，電阻器用於限制電流大小和/或分壓。

設流過電阻器的電流為 I 安培，其兩端的電壓為 V 伏特。下圖顯示了電阻器的**符號**以及電流 I 和電壓 V。

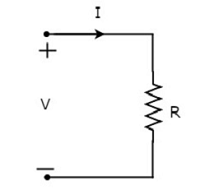
根據**歐姆定律**，電阻器兩端的電壓等於流過它的電流與其電阻的乘積。**數學表示式**為

$V = IR$ 公式 1

$\Rightarrow I = \frac{V}{R}$公式 2

其中，R 為電阻器的電阻。

從公式 2 可以得出，流過電阻器的電流與加在其兩端的電壓成正比，與電阻器的電阻成反比。

電路元件中的**功率**可以表示為

$P = VI$公式 3

將公式 1 代入公式 3。

$P = (IR)I$

$\Rightarrow P = I^2 R$公式 4

將公式 2 代入公式 3。

$P = V \lgroup \frac{V}{R} \rgroup$

$\Rightarrow P = \frac{V^2}{R}$公式 5

因此，我們可以使用公式 3 到 5 中的任何一個公式來計算電阻器上耗散的功率。

電感器

一般來說，電感器會有多個線圈。因此，當電流流過它時，它會產生磁通量。因此，電感器產生的總磁通量取決於流過它的電流 I，它們之間存線上性關係。

**數學表示式**為

$$\Psi \: \alpha \: I$$

$$\Rightarrow \Psi = LI$$

其中，

• Ψ 為總磁通量

• L 為電感器的電感

設流過電感器的電流為I 安培，其兩端的電壓為V 伏特。下圖顯示了電感器的**符號**以及電流I 和電壓V。

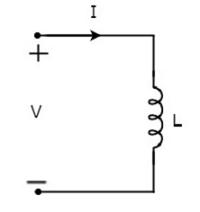
根據**法拉第定律**，電感器兩端的電壓可以寫成

$$V = \frac{d\Psi}{dt}$$

將Ψ = LI 代入上式。

$$V = \frac{d(LI)}{dt}$$

$$\Rightarrow V = L \frac{dI}{dt}$$

$$\Rightarrow I = \frac{1}{L} \int V dt$$

從上述公式可以看出，電感器兩端的電壓與流過它的電流之間存在**線性關係**。

我們知道，電路元件中的**功率**可以表示為

$$P = VI$$

將$V = L \frac{dI}{dt}$代入上式。

$$P = \lgroup L \frac{dI}{dt}\rgroup I$$

$$\Rightarrow P = LI \frac{dI}{dt}$$

透過積分上式，我們可以得到電感器中儲存的**能量**為

$$W = \frac{1}{2} LI^2$$

因此，電感器以磁場的形式儲存能量。

電容器

一般來說，電容器有兩個導電極板，由介電介質隔開。如果在電容器兩端施加正電壓，則它會儲存正電荷。類似地，如果在電容器兩端施加負電壓，則它會儲存負電荷。

因此，電容器中儲存的電荷量取決於施加在其兩端的電壓V，它們之間存線上性關係。數學表示式為

$$Q \: \alpha \: V$$

$$\Rightarrow Q = CV$$

其中，

• Q 為電容器中儲存的電荷。

• C 為電容器的電容。

設流過電容器的電流為I 安培，其兩端的電壓為V 伏特。下圖顯示了電容器的符號以及電流I 和電壓V。

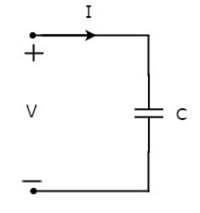
我們知道，**電流**就是**電荷流動的速率**。數學表示式為

$$I = \frac{dQ}{dt}$$

將$Q = CV$代入上式。

$$I = \frac{d(CV)}{dt}$$

$$\Rightarrow I = C \frac{dV}{dt}$$

$$\Rightarrow V = \frac{1}{C} \int I dt$$

從上述公式可以看出，電容器兩端的電壓與流過它的電流之間存在**線性關係**。

我們知道，電路元件中的**功率**可以表示為

$$P = VI$$

將$I = C \frac{dV}{dt}$代入上式。

$$P = V \lgroup C \frac{dV}{dt} \rgroup$$

$$\Rightarrow P = CV \frac{dV}{dt}$$

透過積分上式，我們可以得到電容器中儲存的**能量**為

$$W = \frac{1}{2}CV^2$$

因此，電容器以電場的形式儲存能量。