網路理論 - 星形到三角形轉換

---

---

在上一章中，我們討論了將三角形網路轉換為等效星形網路。現在，讓我們討論如何將星形網路轉換為等效三角形網路。這種轉換稱為星形到三角形轉換。

在上一章中，我們得到了從三角形網路得到的星形網路電阻為

$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ 公式1

$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ 公式2

$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ 公式3

根據星形網路電阻表示的三角形網路電阻

讓我們對上述公式進行變換，以便根據星形網路的電阻得到三角形網路的電阻。

• 相乘每一組兩個公式，然後相加。

$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$

$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$

$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ 公式4

• 用公式2除以公式4，我們將得到

$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$

$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

• 用公式3除以公式4，我們將得到

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

• 用公式1除以公式4，我們將得到

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

利用上述關係，我們可以根據星形網路的電阻找到三角形網路的電阻。透過這種方式，我們可以將星形網路轉換為三角形網路。

示例

讓我們計算三角形網路的電阻，它與下圖所示的星形網路等效。

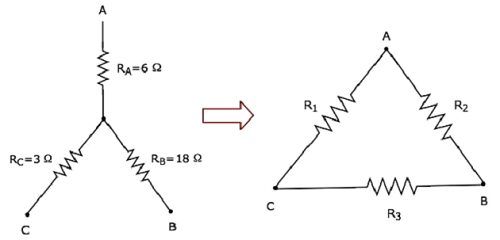
給定星形網路的電阻為R_A = 6 Ω, R_B = 18 Ω和R_C = 3 Ω。

我們知道根據星形網路電阻表示的三角形網路電阻的關係如下。

$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

將R_A, R_B和R_C的值代入上述公式。

$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$

$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$

$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$

因此，我們得到了三角形網路的電阻為R₁ = 10 Ω, R₂ = 60 Ω和R₃ = 30 Ω，它們與給定星形網路的電阻等效。