
- 網路理論教程
- 網路理論 - 首頁
- 網路理論 - 概述
- 例題
- 網路理論 - 有源元件
- 網路理論 - 無源元件
- 網路理論 - 基爾霍夫定律
- 電路量分配原理
- 網路理論 - 節點分析
- 網路理論 - 網孔分析
- 網路理論 - 等效電路
- 等效電路例題
- 三角形到星形轉換
- 星形到三角形轉換
- 網路理論 - 網路拓撲
- 網路拓撲矩陣
- 疊加定理
- 戴維南定理
- 網路理論 - 諾頓定理
- 最大功率傳輸定理
- 直流電路的響應
- 交流電路的響應
- 網路理論 - 串聯諧振
- 並聯諧振
- 網路理論 - 耦合電路
- 二埠網路
- 二埠引數轉換
- 網路理論 - 濾波器
- 網路理論有用資源
- 網路理論 - 快速指南
- 網路理論 - 有用資源
- 網路理論 - 討論
最大功率傳輸定理
負載接收到的功率大小是電力和電子應用中的一個重要引數。在直流電路中,我們可以用一個電阻 RL 歐姆來表示負載。同樣,在交流電路中,我們可以用一個阻抗為 ZL 歐姆的複雜負載來表示它。
最大功率傳輸定理指出,只有當負載電阻等於電源電阻時,直流電壓源才能向可變負載電阻傳遞最大功率。
同樣,最大功率傳輸定理指出,只有當負載阻抗等於電源阻抗的共軛複數時,交流電壓源才能向可變複雜負載傳遞最大功率。
在本章中,讓我們討論一下直流電路的最大功率傳輸定理。
最大功率傳輸定理的證明
將任何二端線性網路或電路替換為可變負載電阻(電阻為 RL 歐姆)左側的戴維南等效電路。我們知道戴維南等效電路類似於一個實際電壓源。
此概念如下圖所示。
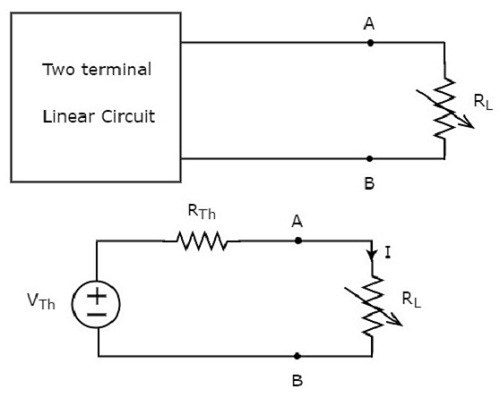
負載電阻上耗散的功率為
$$P_L = I^2 R_L$$
將 $I = \frac{V_{Th}}{R_{Th} + R_L}$ 代入上式。
$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$
$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ 公式1
最大功率傳輸的條件
為了求最大值或最小值,一階導數為零。因此,對公式1關於 RL 求導,並令其等於零。
$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$
$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$
$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$
$$\Rightarrow (R_{Th} - R_L) = 0$$
$$\Rightarrow R_{Th} = R_L\:或\:R_L = R_{Th}$$
因此,負載上最大功率耗散的條件是 $R_L = R_{Th}$。這意味著,如果負載電阻的值等於電源電阻(即戴維南電阻)的值,則負載上耗散的功率將為最大值。
最大功率傳輸的值
將 $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ 代入公式1。
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: 因為 \: R_{L} = R_{Th}$$
因此,傳遞到負載的最大功率為
$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$
最大功率傳輸的效率
我們可以使用以下公式計算最大功率傳輸效率,$\eta_{Max}$。
$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ 公式2
其中,
$P_{L, Max}$ 是傳遞到負載的最大功率。
$P_S$ 是電源產生的功率。
電源產生的功率為
$$P_S = I^2 R_{Th} + I^2 R_L$$
$$\Rightarrow P_S = 2 I^2 R_{Th},\:因為\:R_{L} = R_{Th}$$
將 $I = \frac{V_{Th}}{2 R_{Th}}$ 代入上式。
$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$
$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$
$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$
將 $P_{L, Max}$ 和 $P_S$ 的值代入公式2。
$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$
$$\Rightarrow \eta_{Max} = \frac{1}{2}$$
我們可以用百分比表示最大功率傳輸效率,如下所示:
$$\% \eta_{Max} = \eta_{Max} \times 100\%$$
$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$
$$\Rightarrow \% \eta_{Max} = 50\%$$
因此,最大功率傳輸效率為50%。
示例
求可以傳遞到如下圖所示電路的負載電阻 RL 的最大功率。
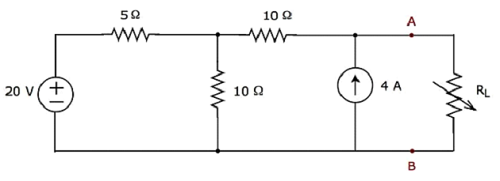
步驟1 - 在戴維南定理章節中,我們計算了 A&B 端子左側的戴維南等效電路。我們現在可以使用此電路。它如下圖所示。
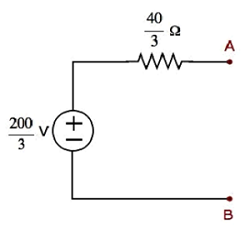
這裡,戴維南電壓 $V_{Th} = \frac{200}{3}V$,戴維南電阻 $R_{Th} = \frac{40}{3} \Omega$
步驟2 - 用上述戴維南等效電路替換給定電路中 A&B 端子左側的部分電路。生成的電路圖如下圖所示。
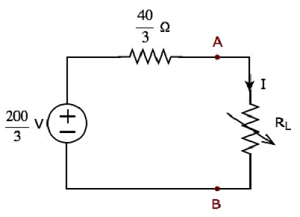
步驟3 - 我們可以使用以下公式找到將傳遞到負載電阻 RL 的最大功率。
$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
將 $V_{Th} = \frac{200}{3}V$ 和 $R_{Th} = \frac{40}{3} \Omega$ 代入上述公式。
$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$
$$P_{L, Max} = \frac{250}{3} W$$
因此,將傳遞到給定電路的負載電阻 RL 的最大功率為 $\mathbf {\frac{250}{3}}$ W