網路理論 - 耦合電路

---

---

當電路中存在的線圈（或電感器）之間存在互感時，該電路被稱為耦合電路。線圈不過是電阻和電感器的串聯組合。在沒有電阻的情況下，線圈變成電感器。有時，線圈和電感器這兩個術語可以互換使用。

在本章中，我們首先討論點約定，然後討論耦合的分類。

點約定

點約定是一種技術，它提供了有關帶點端子上電壓極性的詳細資訊。此資訊在編寫 KVL 方程時非常有用。

• 如果電流進入一個線圈（或電感器）的帶點端子，則它會在另一個線圈（或電感器）上感應出一個電壓，該電壓在帶點端子上具有正極性。

• 如果電流離開一個線圈（或電感器）的帶點端子，則它會在另一個線圈（或電感器）上感應出一個電壓，該電壓在帶點端子上具有負極性。

耦合的分類

我們可以將耦合分為以下兩類。

• 電耦合
• 磁耦合

現在，讓我們逐一討論每種型別的耦合。

電耦合

當兩個線圈（或電感器）之間存在物理連線時，就會發生電耦合。這種耦合可以是互助型或相反型。它取決於電流是進入帶點端子還是離開帶點端子。

互助型耦合

考慮以下電路線路，其中有兩個串聯連線的電感器。

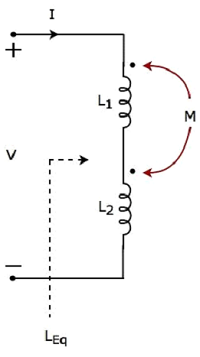
由於兩個電感器是串聯連線的，因此相同的電流I流過兩個自感分別為 L₁ 和 L₂ 的電感器。

在這種情況下，電流 I 進入每個電感器的帶點端子。因此，由於另一個線圈中的電流，每個電感器中的感應電壓在其帶點端子上將具有正極性。

在上述電路線路或網路的迴路周圍應用KVL。

$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$

$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$

$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$

上述方程的形式為 $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

因此，上圖所示的電感器串聯組合的等效電感為

$$L_{Eq} = L_1 + L_2 + 2M$$

在這種情況下，等效電感增加了 2M。因此，上述電路是電耦合的互助型示例。

相反型耦合

考慮以下電路線路，其中有兩個串聯連線的電感器。

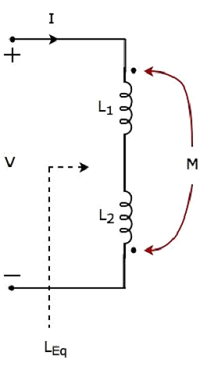
在上圖電路中，電流I進入自感為L₁的電感器的帶點端子。因此，它在另一個自感為L₂的電感器中感應出電壓。因此，該電感器的帶點端子上存在感應電壓的正極性。

在上圖電路中，電流I離開自感為L₂的電感器的帶點端子。因此，它在另一個自感為L₁的電感器中感應出電壓。因此，該電感器的帶點端子上存在感應電壓的負極性。

在上述電路線路或網路的迴路周圍應用KVL。

$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$

$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$

$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$

上述方程的形式為 $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

因此，上圖所示的電感器串聯組合的等效電感為

$$L_{Eq} = L_1 + L_2 - 2M$$

在這種情況下，等效電感減少了 2M。因此，上述電路是電耦合的相反型示例。

磁耦合

當兩個線圈（或電感器）之間沒有物理連線時，就會發生磁耦合。這種耦合可以是互助型或相反型。它取決於電流是進入帶點端子還是離開帶點端子。

互助型耦合

考慮以下變壓器的電等效電路。它有兩個線圈，分別稱為初級線圈和次級線圈。

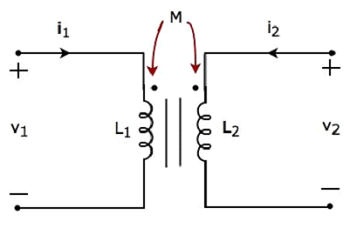
流過初級和次級線圈的電流分別為 i₁ 和 i₂。在這種情況下，這些電流進入各自線圈的帶點端子。因此，由於另一個線圈中的電流，每個線圈中的感應電壓在其帶點端子上將具有正極性。

在初級線圈周圍應用KVL。

$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$方程 1

在次級線圈周圍應用KVL。

$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$方程 2

在方程 1 和方程 2 中，自感電壓和互感電壓具有相同的極性。因此，上述變壓器電路是磁耦合的互助型示例。

相反型耦合

考慮以下變壓器的電等效電路。

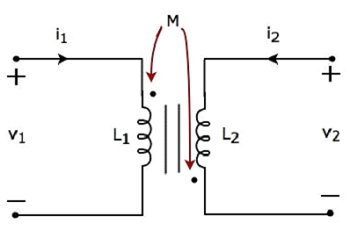
流過初級和次級線圈的電流分別為 i₁ 和 i₂。在這種情況下，電流 i₁ 進入初級線圈的帶點端子。因此，它在次級線圈中感應出電壓。因此，該次級線圈的帶點端子上存在感應電壓的正極性。

在上圖電路中，電流 i₂ 離開次級線圈的帶點端子。因此，它在初級線圈中感應出電壓。因此，該初級線圈的帶點端子上存在感應電壓的負極性。

在初級線圈周圍應用KVL。

$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$方程 3

在次級線圈周圍應用KVL。

$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$方程 4

在方程 3 和方程 4 中，自感電壓和互感電壓具有相反的極性。因此，上述變壓器電路是磁耦合的相反型示例。