網路理論 - 等效電路

---

---

如果一個電路由兩個或多個類似的無源元件組成，並且這些元件僅以串聯或並聯的方式連線，那麼我們可以用一個單獨的等效無源元件來替換它們。因此，該電路被稱為等效電路。

在本章中，讓我們討論以下兩種等效電路。

• 串聯等效電路
• 並聯等效電路

串聯等效電路

如果類似的無源元件串聯連線，則相同的電流將流過所有這些元件。但是，電壓在每個元件上都會被分壓。

請考慮以下電路圖。

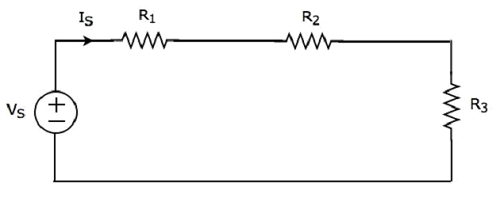
它有一個電壓源 (V_S) 和三個電阻，電阻值為 R₁、R₂ 和 R₃。所有這些元件都串聯連線。電流 IS 流過所有這些元件。

上述電路只有一個網孔。該網孔的KVL 方程為

$$V_S = V_1 + V_2 + V_3$$

將 $V_1 = I_S R_1, \: V_2 = I_S R_2$ 和 $V_3 = I_S R_3$ 代入上述方程。

$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$

$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$

上述方程的形式為 $V_S = I_S R_{Eq}$，其中，

$$R_{Eq} = R_1 + R_2 + R_3$$

給定電路的等效電路圖如下所示。

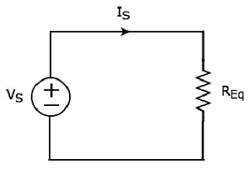
這意味著，如果多個電阻串聯連線，則可以用一個等效電阻來代替它們。該等效電阻的阻值等於所有這些多個電阻阻值的總和。

注 1 - 如果 'N' 個電感，其電感值為 L₁、L₂、...、L_N 串聯連線，則等效電感將為

$$L_{Eq} = L_1 + L_2 + ... + L_N$$

注 2 - 如果 'N' 個電容，其電容值為 C₁、C₂、...、C_N 串聯連線，則等效電容將為

$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$

並聯等效電路

如果類似的無源元件並聯連線，則相同的電壓將保持在每個元件上。但是，流過每個元件的電流將被分流。

請考慮以下電路圖。

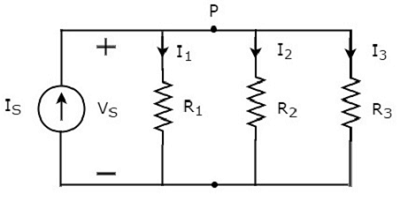
它有一個電流源 (I_S) 和三個電阻，電阻值為 R₁、R₂ 和 R₃。所有這些元件都並聯連線。電壓 (V_S) 可用於所有這些元件。

上述電路只有一個主節點 (P)，除了接地節點。該主節點 (P) 的KCL 方程為

$$I_S = I_1 + I_2 + I_3$$

將 $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ 和 $I_3 = \frac{V_S}{R_3}$ 代入上述方程。

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$

$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$

$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$

上述方程的形式為 V_S = I_SR_Eq，其中，

$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$

$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$

給定電路的等效電路圖如下所示。

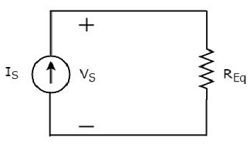
這意味著，如果多個電阻並聯連線，則可以用一個等效電阻來代替它們。該等效電阻的阻值等於所有這些多個電阻的每個電阻阻值倒數之和的倒數。

注 1 - 如果 'N' 個電感，其電感值為 L₁、L₂、...、L_N 並聯連線，則等效電感將為

$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$

注 2 - 如果 'N' 個電容，其電容值為 C₁、C₂、...、C_N 並聯連線，則等效電容將為

$$C_{Eq} = C_1 + C_2 + ... + C_N$$