網路理論 - 網路拓撲

---

---

網路拓撲是電氣電路的圖形表示。它透過將複雜的電氣電路轉換為網路圖來分析這些電路。網路拓撲也稱為**圖論**。

網路拓撲的基本術語

現在，讓我們討論一下網路拓撲中涉及的基本術語。

圖

網路圖簡稱為**圖**。它由一組透過分支連線的節點組成。在圖中，節點是兩個或多個分支的公共點。有時，只有一個分支可能連線到節點。分支是連線兩個節點的線段。

任何電氣電路或網路都可以透過用短路代替無源元件和電壓源，用開路代替電流源，將其轉換為等效的**圖**。這意味著圖中的線段表示對應於電氣電路的無源元件或電壓源的分支。

示例

讓我們考慮以下**電氣電路**。

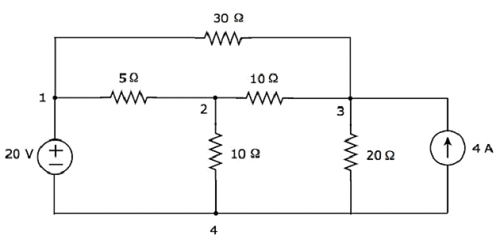
在上圖中，有**四個主節點**，分別標記為 1、2、3 和 4。在上圖中，有**七個分支**，其中一個分支包含一個 20 V 的電壓源，另一個分支包含一個 4 A 的電流源，其餘五個分支包含電阻，電阻值分別為 30 Ω、5 Ω、10 Ω、10 Ω 和 20 Ω。

與上述電氣電路對應的等效**圖**如下所示。

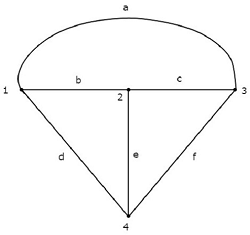
在上圖中，有**四個節點**，分別標記為 1、2、3 和 4。它們與電氣電路中的主節點相同。上圖中有**六個分支**，分別標記為 a、b、c、d、e 和 f。

在這種情況下，我們在圖中**少了一個分支**，因為在將電氣電路轉換為等效圖時，4 A 的電流源被視為開路。

從這個例子中，我們可以得出以下結論 -

• 圖中存在的**節點數**將等於電氣電路中存在的主節點數。

• 圖中存在的**分支數**將小於或等於電氣電路中存在的分支數。

圖的型別

以下是圖的型別 -

• 連通圖
• 非連通圖
• 有向圖
• 無向圖

現在，讓我們逐一討論這些圖。

連通圖

如果圖的任意兩個節點之間至少存在一個分支，則稱為**連通圖**。這意味著連通圖中的每個節點都將有一個或多個連線到它的分支。因此，沒有節點會以孤立或分離的形式出現。

前面示例中顯示的圖是**連通圖**。在這裡，所有節點都由三個分支連線。

非連通圖

如果圖中至少存在一個節點，即使單個分支也沒有連線到它，則稱為**非連通圖**。因此，非連通圖中將存在一個或多個孤立節點。

考慮下圖所示的圖。

在此圖中，節點 2、3 和 4 由兩個分支連線。但是，甚至沒有一個分支連線到**節點 1**。因此，節點 1 成為**孤立節點**。因此，上圖是**非連通圖**。

有向圖

如果圖的所有分支都用箭頭表示，則該圖稱為**有向圖**。這些箭頭表示每個分支中電流流動的方向。因此，此圖也稱為**定向圖**。

考慮下圖所示的圖。

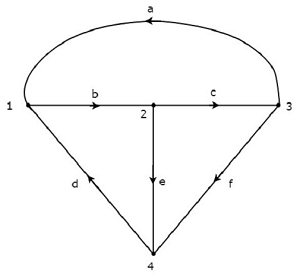
在上圖中，每個分支中電流流動的方向都用箭頭表示。因此，它是一個**有向圖**。

無向圖

如果圖的分支沒有用箭頭表示，則該圖稱為**無向圖**。由於沒有電流流動的方向，因此此圖也稱為**無定向圖**。

本章第一個示例中顯示的圖是**無定向圖**，因為該圖的分支上沒有箭頭。

子圖及其型別

圖的一部分稱為**子圖**。我們透過移除給定圖的一些節點和/或分支來獲得子圖。因此，子圖的分支和/或節點數將小於原始圖。因此，我們可以得出結論，子圖是圖的子集。

以下是子圖的**兩種型別**。

• 樹
• 餘樹

樹

樹是給定圖的連通子圖，它包含圖的所有節點。但是，該子圖中不應該有任何迴路。樹的分支稱為**樹枝**。

考慮以下本章開頭示例中所示的圖的**連通子圖**。

此連通子圖包含給定圖的所有四個節點，並且沒有迴路。因此，它是一棵**樹**。

此樹只有三個分支，而不是給定圖的六個分支。因為，如果我們考慮給定圖的其餘分支中的任何一個分支，那麼上述連通子圖中將會有一個迴路。然後，生成的連通子圖將不是樹。

從上面的樹中，我們可以得出結論，樹中存在的**分支數**應等於**n - 1**，其中“n”是給定圖的節點數。

餘樹

餘樹是在形成樹時移除的分支形成的子圖。因此，它稱為樹的**補圖**。對於每棵樹，都將有一個相應的餘樹，其分支稱為**連支**或弦。通常，連支用虛線表示。

與上述樹對應的**餘樹**如下所示。

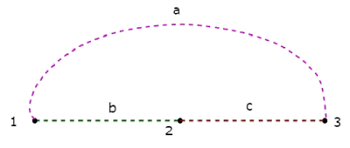
此餘樹只有三個節點，而不是給定圖的四個節點，因為節點 4 與上述餘樹隔離。因此，餘樹不必是連通子圖。此餘樹有三個分支，它們形成一個迴路。

餘樹中存在的**分支數**將等於給定圖的分支數與樹枝數之差。在數學上，可以寫成

$$l = b - (n - 1)$$

$$l = b - n + 1$$

其中，

• l 是連支數。
• b 是給定圖中存在的分支數。
• n 是給定圖中存在的節點數。

如果我們將樹及其對應的餘樹組合起來，我們將得到如下所示的**原始圖**。

樹枝 d、e 和 f 用實線表示。餘樹分支 a、b 和 c 用虛線表示。