網路理論 - 基爾霍夫定律

---

---

網路元件可以是有源或無源型別。任何電路或網路都包含這兩種型別的網路元件之一或兩者結合。

現在，讓我們討論以下兩個定律，它們通常被稱為基爾霍夫定律。

• 基爾霍夫電流定律
• 基爾霍夫電壓定律

基爾霍夫電流定律

基爾霍夫電流定律 (KCL) 指出，離開（或進入）節點的所有電流的代數和等於零。

節點是指兩個或多個電路元件連線在一起的點。如果只有兩個電路元件連線到一個節點，則稱為簡單節點。如果三個或更多電路元件連線到一個節點，則稱為主節點。

數學上，KCL 可以表示為

$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$

其中，

• I_m 是離開節點的第 m 個支路電流。

• M 是連線到節點的支路數量。

上述KCL的陳述也可以表示為“進入節點的所有電流的代數和等於離開節點的所有電流的代數和”。讓我們透過以下示例來驗證此陳述。

示例

在以下圖形的節點P處寫出KCL 方程。

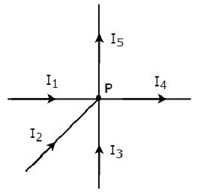
• 在上圖中，支路電流 I₁、I₂ 和 I₃ 進入節點 P。因此，對這三個電流考慮負號。

• 在上圖中，支路電流 I₄ 和 I₅ 離開節點 P。因此，對這兩個電流考慮正號。

節點 P 處的KCL 方程將是

$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$

$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$

在上式中，左側表示進入電流的總和，而右側表示離開電流的總和。

在本教程中，當電流離開節點時，我們將考慮正號，而當電流進入節點時，我們將考慮負號。同樣，您可以考慮當電流離開節點時使用負號，而當電流進入節點時使用正號。在這兩種情況下，結果都相同。

注意 - KCL 與連線到節點的網路元件的性質無關。

基爾霍夫電壓定律

基爾霍夫電壓定律 (KVL) 指出，圍繞回路或網孔的所有電壓的代數和等於零。

迴路是指從同一個節點開始並終止於同一個節點的路徑。相比之下，網孔是指不包含任何其他迴路的迴路。

數學上，KVL 可以表示為

$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$

其中，

• V_n 是迴路（網孔）中第 n 個元件的電壓。

• N 是迴路（網孔）中網路元件的數量。

上述KVL的陳述也可以表示為“電壓源的代數和等於迴路中存在的電壓降的代數和”。讓我們藉助以下示例來驗證此陳述。

示例

在以下電路的迴路周圍寫出KVL 方程。

上述電路圖由一個電壓源 V_S 與兩個電阻 R₁ 和 R₂ 串聯組成。電阻 R₁ 和 R₂ 上的電壓降分別為 V₁ 和 V₂。

圍繞回路應用KVL。

$$V_S - V_1 - V_2 = 0$$

$$\Rightarrow V_S = V_1 + V_2$$

在上式中，左側項表示單個電壓源 VS。而右側表示電壓降的總和。在這個例子中，我們只考慮了一個電壓源。因此，左側只包含一項。如果我們考慮多個電壓源，則左側包含電壓源的總和。

在本教程中，我們考慮每個元件電壓的符號作為圍繞回路行進時存在的第二個端子的極性。同樣，您可以考慮每個電壓的符號作為圍繞回路行進時存在的第一個端子的極性。在這兩種情況下，結果都相同。

注意 - KVL 與迴路中存在的網路元件的性質無關。