等效電路例題

在上一章中，我們討論了串聯組合和並聯組合的等效電路。本章我們透過考慮相似無源元件的串聯和並聯組合來解決一個例題。

例題

讓我們求解以下電路網路中A&B兩端之間的等效電阻。

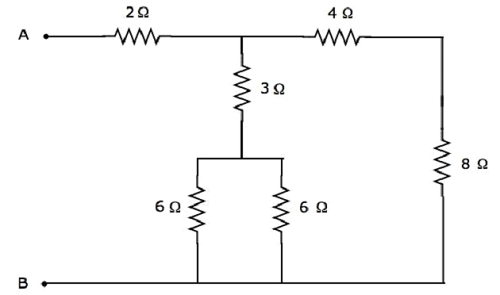
我們將透過將上述網路簡化為這兩端之間的一個單一電阻來得到A&B兩端之間的等效電阻。為此，我們必須識別以串聯和並聯形式連線的電阻組合，然後在每一步中找到各自形式的等效電阻。

給定的電路網路被修改成如下所示的形式。

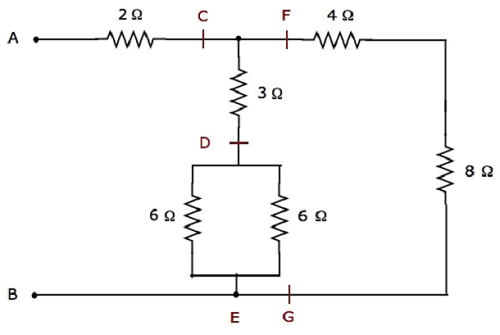
在上圖中，字母C到G用於標記各個節點。

步驟1 - 在上述網路中，兩個6 Ω電阻並聯連線。因此，D&E之間的等效電阻將為3 Ω。這可以透過以下簡化得到。

$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$

在上圖網路中，4 Ω和8 Ω的電阻串聯連線。因此，F&G之間的等效電阻將為12 Ω。這可以透過以下簡化得到。

$$R_{FG} = 4 + 8 = 12 \Omega$$

步驟2 - 步驟1之後簡化的電路網路如下圖所示。

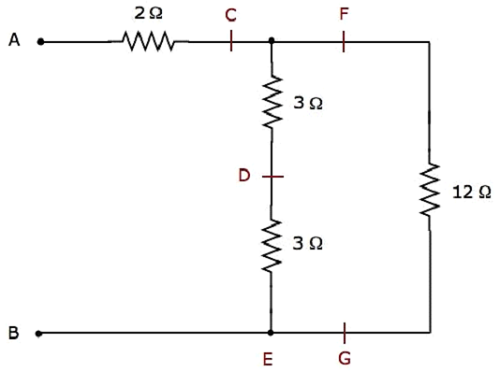
在上圖網路中，兩個3 Ω電阻串聯連線。因此，C&E之間的等效電阻將為6 Ω。這可以透過以下簡化得到。

$$R_{CE} = 3 + 3 = 6 \Omega$$

步驟3 - 步驟2之後簡化的電路網路如下圖所示。

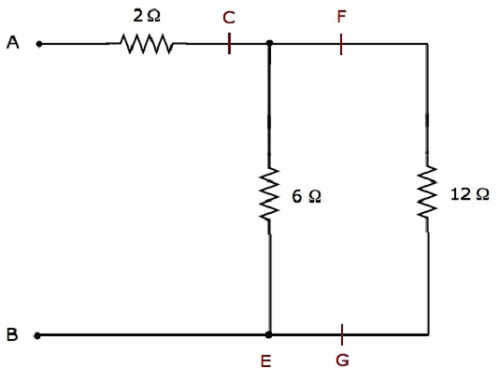
在上圖網路中，6 Ω和12 Ω的電阻並聯連線。因此，C&B之間的等效電阻將為4 Ω。這可以透過以下簡化得到。

$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$

步驟4 - 步驟3之後簡化的電路網路如下圖所示。

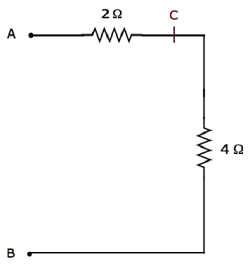
在上圖網路中，2 Ω和4 Ω的電阻在A&B端之間串聯連線。因此，A&B之間的等效電阻將為6 Ω。這可以透過以下簡化得到。

$$R_{AB} = 2 + 4 = 6 \Omega$$

因此，給定電路網路中A&B兩端之間的等效電阻為6 Ω。