網路理論 - 直流電路的響應

---

---

如果電迴路的輸出對於輸入隨時間變化，則稱為時間響應。時間響應包含以下兩個部分。

• 暫態響應
• 穩態響應

在本章中，首先讓我們討論這兩個響應，然後觀察串聯RL電路在直流電壓源激勵下的這兩個響應。

暫態響應

對電迴路施加輸入後，輸出需要一定時間才能達到穩態。因此，輸出將處於暫態狀態，直到它進入穩態。因此，電迴路在暫態狀態下的響應稱為暫態響應。

對於較大的“t”值，暫態響應將為零。理想情況下，此“t”值應為無窮大。但是，實際上五個時間常數就足夠了。

暫態的存在與否

由於施加到電迴路的電源的突然變化和/或由於開關動作，響應中會出現暫態。存在兩種可能的開關動作。分別是開啟開關和閉合開關。

• 如果電迴路或網路僅包含電阻，則電迴路或網路的響應中不會出現暫態部分。因為電阻能夠調節任意數量的電壓和電流。

• 由於存在儲能元件，如電感和電容，因此電迴路或網路的響應中會出現暫態部分。因為它們不能立即改變儲存在這些元件中的能量。

電感器的行為

假設開關動作發生在t = 0 時。當開關動作發生時，電感電流不會瞬時變化。這意味著，開關動作後的電感電流值將與開關動作前的值相同。

數學上，它可以表示為

$$i_L (0^+) = i_L (0^-)$$

電容器的行為

當開關動作發生時，電容電壓不會像電感電流那樣瞬時變化。這意味著，開關動作後的電容電壓值將與開關動作前的值相同。

數學上，它可以表示為

$$v_c (0^+) = v_c (0^-)$$

穩態響應

即使在暫態響應對於較大的“t”值變為零後仍然存在的時域響應部分稱為穩態響應。這意味著，在穩態期間響應中將沒有任何暫態部分。

電感器的行為

如果獨立電源連線到具有一個或多個電感和電阻（可選）的電迴路或網路很長時間，則該電迴路或網路被稱為處於穩態。因此，該電迴路中電感器的儲能達到最大且恆定。

數學上，它可以表示為

$W_L = \frac{L {i_L}^2}{2} = $ 最大且恆定

$\Rightarrow i_L = $ 最大且恆定

因此，電感在穩態下充當恆流源。

電感兩端的電壓將為

$$V_L = L \frac{di_{L}}{dt} = 0V$$

因此，電感在穩態下充當短路。

電容器的行為

如果獨立電源連線到具有一個或多個電容和電阻（可選）的電迴路或網路很長時間，則該電迴路或網路被稱為處於穩態。因此，該電迴路中電容器的儲能達到最大且恆定。

數學上，它可以表示為

$W_c = \frac{C{v_c}^2}{2} = $ 最大且恆定

$\Rightarrow v_c = $最大且恆定

因此，電容在穩態下充當恆壓源。

流過電容的電流將為

$$i_c = C\frac{dv_c}{dt} = 0A$$

因此，電容在穩態下充當開路。

求解串聯RL電路的響應

考慮以下串聯RL電路圖。

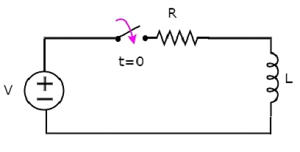
在上述電路中，開關一直保持開啟狀態，直到 t = 0，並在 t = 0 時閉合。因此，電壓為 V伏特的直流電壓源在此之前未連線到串聯RL電路。因此，沒有初始電流流過電感。

開關處於閉合位置時的電路圖如下所示。

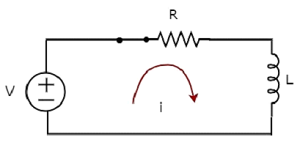
現在，由於電壓為V伏特的直流電壓源已連線到串聯RL電路，因此電流i流經整個電路。

現在，對迴路應用KVL。

$$V = Ri + L \frac{di}{dt}$$

$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$公式 1

上述公式是一階微分公式，其形式為

$\frac{dy}{dt} + Py = Q$公式 2

透過比較公式 1 和公式 2，我們將得到以下關係。

$$x = t$$

$$y = i$$

$$P = \frac{R}{L}$$

$$Q = \frac{V}{L}$$

公式 2 的解將為

$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$公式 3

其中，k 為常數。

將 x、y、P 和 Q 的值代入公式 3。

$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$

$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$公式 4

我們知道電路中沒有初始電流。因此，為了找到常數k的值，請在公式 4 中代入t = 0 和𝑖 = 0。

$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$

$$0 = \frac{V}{R} + k(1)$$

$$k = - \frac{V}{R}$$

將 k 的值代入公式 4。

$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$

$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$

因此，流過電路的電流為

$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$公式 5

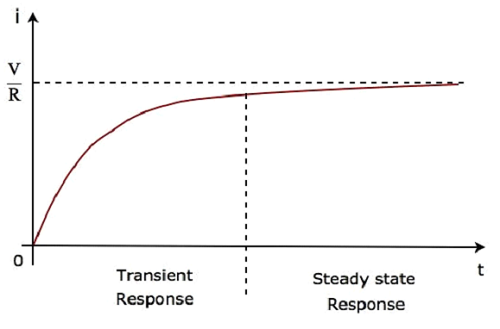
因此，當串聯RL電路由直流電壓源激勵時，其響應具有以下兩項。

• 第一項$-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$對應於暫態響應。

• 第二項$\frac{V}{R}$對應於穩態響應。這兩項響應如下圖所示。

我們可以如下重新編寫公式 5 −

$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$

$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$公式 6

其中，τ 為時間常數，其值等於$\frac{L}{R}$。

公式 5 和公式 6 是相同的。但是，透過在公式 6 中代入一些t的值（如 0、τ、2τ、5τ 等），我們可以輕鬆理解上述流過電路的電流波形。

在上述流過電路的電流波形中，暫態響應從零開始存在，直到五個時間常數，而穩態響應從五個時間常數開始存在。