
- 密碼學教程
- 密碼學 - 首頁
- 密碼學 - 起源
- 密碼學 - 歷史
- 密碼學 - 原理
- 密碼學 - 應用
- 密碼學 - 優點與缺點
- 密碼學 - 現代
- 密碼學 - 傳統密碼
- 密碼學 - 加密的需求
- 密碼學 - 雙重強度加密
- 密碼系統
- 密碼系統
- 密碼系統 - 元件
- 密碼系統的攻擊
- 密碼系統 - 彩虹表攻擊
- 密碼系統 - 字典攻擊
- 密碼系統 - 暴力破解攻擊
- 密碼系統 - 密碼分析技術
- 密碼學的型別
- 密碼系統 - 型別
- 公鑰加密
- 現代對稱金鑰加密
- 密碼學雜湊函式
- 金鑰管理
- 密碼系統 - 金鑰生成
- 密碼系統 - 金鑰儲存
- 密碼系統 - 金鑰分發
- 密碼系統 - 金鑰撤銷
- 分組密碼
- 密碼系統 - 流密碼
- 密碼學 - 分組密碼
- 密碼學 - Feistel分組密碼
- 分組密碼的工作模式
- 分組密碼的工作模式
- 電子密碼本(ECB)模式
- 密碼分組連結(CBC)模式
- 密碼反饋(CFB)模式
- 輸出反饋(OFB)模式
- 計數器(CTR)模式
- 經典密碼
- 密碼學 - 反向密碼
- 密碼學 - 凱撒密碼
- 密碼學 - ROT13演算法
- 密碼學 - 換位密碼
- 密碼學 - 加密換位密碼
- 密碼學 - 解密換位密碼
- 密碼學 - 乘法密碼
- 密碼學 - 仿射密碼
- 密碼學 - 簡單替換密碼
- 密碼學 - 簡單替換密碼的加密
- 密碼學 - 簡單替換密碼的解密
- 密碼學 - 維吉尼亞密碼
- 密碼學 - 維吉尼亞密碼的實現
- 現代密碼
- Base64編碼與解碼
- 密碼學 - XOR加密
- 替換技術
- 密碼學 - 單字母替換密碼
- 密碼學 - 單字母替換密碼的破解
- 密碼學 - 多字母替換密碼
- 密碼學 - Playfair密碼
- 密碼學 - 希爾密碼
- 多字母替換密碼
- 密碼學 - 一次性密碼本密碼
- 一次性密碼本密碼的實現
- 密碼學 - 換位技術
- 密碼學 - 柵欄密碼
- 密碼學 - 列移位密碼
- 密碼學 - 隱寫術
- 對稱演算法
- 密碼學 - 資料加密
- 密碼學 - 加密演算法
- 密碼學 - 資料加密標準
- 密碼學 - 三重DES
- 密碼學 - 雙重DES
- 高階加密標準
- 密碼學 - AES結構
- 密碼學 - AES變換函式
- 密碼學 - 位元組替換變換
- 密碼學 - 行移位變換
- 密碼學 - 列混合變換
- 密碼學 - 輪金鑰加變換
- 密碼學 - AES金鑰擴充套件演算法
- 密碼學 - Blowfish演算法
- 密碼學 - SHA演算法
- 密碼學 - RC4演算法
- 密碼學 - Camellia加密演算法
- 密碼學 - ChaCha20加密演算法
- 密碼學 - CAST5加密演算法
- 密碼學 - SEED加密演算法
- 密碼學 - SM4加密演算法
- IDEA - 國際資料加密演算法
- 公鑰(非對稱)密碼學演算法
- 密碼學 - RSA演算法
- 密碼學 - RSA加密
- 密碼學 - RSA解密
- 密碼學 - 建立RSA金鑰
- 密碼學 - 破解RSA密碼
- 密碼學 - ECDSA演算法
- 密碼學 - DSA演算法
- 密碼學 - Diffie-Hellman演算法
- 密碼學中的資料完整性
- 密碼學中的資料完整性
- 訊息認證
- 密碼學數字簽名
- 公鑰基礎設施
- 雜湊
- MD5(訊息摘要演算法5)
- SHA-1(安全雜湊演算法1)
- SHA-256(安全雜湊演算法256位)
- SHA-512(安全雜湊演算法512位)
- SHA-3(安全雜湊演算法3)
- 雜湊密碼
- Bcrypt雜湊模組
- 現代密碼學
- 量子密碼學
- 後量子密碼學
- 密碼學協議
- 密碼學 - SSL/TLS協議
- 密碼學 - SSH協議
- 密碼學 - IPsec協議
- 密碼學 - PGP協議
- 影像與檔案加密
- 密碼學 - 影像
- 密碼學 - 檔案
- 隱寫術 - 影像
- 檔案加密和解密
- 密碼學 - 檔案加密
- 密碼學 - 檔案解密
- 物聯網中的密碼學
- 物聯網安全挑戰、威脅和攻擊
- 物聯網安全的密碼學技術
- 物聯網裝置的通訊協議
- 常用的密碼學技術
- 自定義構建密碼學演算法(混合密碼學)
- 雲密碼學
- 量子密碼學
- 密碼學中的影像隱寫術
- DNA密碼學
- 密碼學中的一次性密碼(OTP)演算法
- 之間的區別
- 密碼學 - MD5與SHA1
- 密碼學 - RSA與DSA
- 密碼學 - RSA與Diffie-Hellman
- 密碼學與密碼學
- 密碼學 - 密碼學與密碼分析
- 密碼學 - 經典與量子
- 密碼學與隱寫術
- 密碼學與加密
- 密碼學與網路安全
- 密碼學 - 流密碼與分組密碼
- 密碼學 - AES與DES密碼
- 密碼學 - 對稱與非對稱
- 密碼學有用資源
- 密碼學 - 快速指南
- 密碼學 - 討論
SHA-3(安全雜湊演算法3)
資訊安全技術的新模型被稱為SHA-3。這是一段程式碼,可以加密資訊並使其對任何沒有金鑰的人不可讀。SHA-1和SHA-2等先前版本中的基本功能與SHA-3不同。
SHA-3是稱為Keccak的一組更大的秘密程式碼工具的一部分。該小組由Guido Bertoni、Joan Daemen、Michael Peeters和Gilles Van Assche等人建立,他們在名為RadioGatun的基礎上進行了構建。他們讓Keccak執行更多操作,例如為訊息建立秘密程式碼,並在透過網際網路傳送資訊時保護資訊安全。
Keccak以一種稱為海綿構造的獨特方式工作。它就像一塊海綿,可以吸收任意數量的水(或資料),也可以擠出任意數量的水。它可以混合資料,以便在沒有金鑰的情況下沒有人能夠理解它。這使得它非常靈活和有用。
儘管SHA-3相對較新,但較舊的演算法SHA-1和SHA-2仍在使用。但如果需要,SHA-3可以直接替換它們。SHA-3的目標是使秘密程式碼更強大,並總體上更好。
對於小型訊息,有一個名為KangarooTwelve的更快版本。它可以更快地處理短訊息,並且具有特殊的設定使其工作得更好。
SHA-3系列有六個雜湊函式,其摘要(雜湊值)為128、224、256、384或512位:SHA3-224、SHA3-256、SHA3-384、SHA3-512、SHAKE128和SHAKE256。
此庫與上面列出的每種演算法相容。
- SHA3-224,28位摘要大小
- SHA3-256,32位摘要大小
- SHA3-384,48位摘要大小
- SHA3-512,64位摘要大小
- SHAKE-128
- SHAKE-256
SHA-3的歷史
Keccak演算法基於早期稱為PANAMA和RadioGatun的演算法,由Guido Bertoni、Joan Daemen、Michael Peeters和Gilles Van Assche開發。Daemen和Craig Clapp於1998年建立了PANAMA。後來,在2006年,Daemen、Peeters和Van Assche推出了RadioGatun,這是PANAMA的升級版本。
美國國家標準與技術研究院(NIST)於2006年釋出了一場競賽,以擴充套件SHA-3,這是一種廣為人知的秘密程式碼。以前的秘密演算法(如MD5、SHA-0和SHA-1)不再安全,因此為了為SHA-2提供機會,進行了此操作。
Keccak是競賽的51個參賽作品之一。在經過幾輪測試和改進後,它於2010年12月進入決賽。在競賽期間,Keccak進行了修改以提高其強度和安全性。
2012年10月2日,Keccak被選中作為競賽的支持者。NIST於2014年釋出了FIPS 202“SHA-3標準:基於置換的雜湊和可擴充套件輸出函式”的草案。該草案於2015年8月5日獲得批准,使SHA-3成為正式的雜湊標準。
SHA-3的設計
SHA-3的設計使用一種稱為海綿構造的方法。以下是它的工作原理:
- 吸收階段 - 在此步驟中,“海綿”吸收資訊。一個稱為f的轉換函式用於將每塊資料與海綿當前狀態的一部分組合。此函式重新排列狀態的元件。“速率”指的是狀態與輸入/輸出互動的程度,而“容量”指的是保持不變的狀態的程度。系統的安全性取決於其容量。
- 擠壓階段 - 在擠壓階段,轉換函式f在從狀態的同一子集中讀取輸出塊之間交替。要修改輸出的長度,請更改函式的引數。
SHA-3的內部狀態是一個單詞網格,每個單詞都有固定數量的位。此網格的大小影響演算法的整體安全性。SHA-3的不同版本允許不同的輸出長度和字大小,使其適合各種安全需求。
一些SHA-3示例(如SHA3-224、SHA3-256、SHA3-384和SHA3-512)的輸出長度小於速率,因此在擠壓階段不需要額外的轉換。但是,對於SHAKE128和SHAKE256等版本(允許不同的輸出長度),需要進行更多更改才能產生所需的結果。
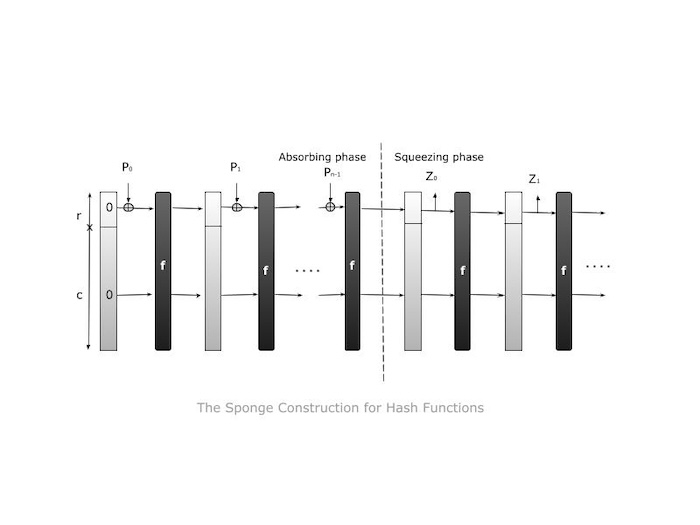
以下是海綿構造的工作原理概述:
- 輸入字串N用一個名為pad的函式進行填充。這確保了填充字串P的長度可以被速率r整除,表示為len(P)/r = n,其中len(P)是P的長度。
- 然後,填充字串P被分成n個連續的塊,每個塊包含r位。這些塊被標識為P0、P1、...和Pn-1。
- 狀態S被初始化為b個零位字串,其中b是狀態的總寬度。
- 每個塊Pi都在末尾擴充套件了一個c個零位字串,其中c等於b - r。這將建立一個長度為b的塊。然後,此擴充套件塊與當前狀態S進行異或運算。之後,將塊置換函式f應用於結果以生成新的狀態S。
- 輸出字串Z被設定為空字串。當Z的長度小於d(所需的輸出長度)時,當前狀態S的前r位將新增到Z中。如果Z仍然小於d位,則f將再次應用於S以生成新的狀態S。此操作將持續進行,直到Z達到所需的長度d。
- 最後,如果Z大於d位,則將其截斷以獲得最終結果。
在SHA-3中,內部狀態S被定義為5×5的單詞網格,每個單詞寬w位。在SHA-3中,w設定為64,總狀態大小為1600位(5×5×64 = 1600)。
但是Keccak允許各種字大小,從w = 1位開始,總狀態大小為25位。字大小的靈活性使得能夠使用較小的狀態大小測試密碼分析攻擊,以及使用從w = 8(200位)到w = 32(800位)的中間狀態大小的實際實現。
在一些SHA-3實現中,例如SHA3-224、SHA3-256、SHA3-384和SHA3-512,速率r(用於吸收輸入的狀態部分)大於所需的輸出長度d。在這些情況下,在擠壓步驟期間不需要進行進一步的塊置換。相反,狀態的前d位給出了所需的雜湊輸出。
另一方面,SHAKE128 和 SHAKE256 允許任意長度的輸出。此功能在諸如最優非對稱加密填充之類的應用中非常有用,在這些應用中,輸出長度必須自定義以滿足特定要求。
SHA-3 變體的示例
假設我們有一個明文為“Tutorialspoint”,那麼根據 SHA-3 變體的雜湊值如下所示:
SHA3-224
此變體生成一個 224 位的雜湊值。“Tutorialspoint” 的雜湊值為 - b3b059b134b17b4bed361b16392b40b16648695eabbf87896c0f8e50
SHA3-256
此變體生成一個 256 位的雜湊值。“Tutorialspoint” 的雜湊值為 - a789f0a2eb3b13ec69245210b8c522bbb7c33ccb0561729697294bcd35367622
SHA3-384
此變體生成一個 384 位的雜湊值。“Tutorialspoint” 的雜湊值為 - 68ccee414159dc755f8aa17d82bd1958c956cd09ecf9a221b661c93ce7b36e40237cbadddf48a0600e1eda4ecdd87295
SHA3-512
此變體生成一個 512 位的雜湊值。“Tutorialspoint” 的雜湊值為 - fb3e821c3a16c720f1137673c6d4247f26e88889093831cf4ca2bb1ef7e0ce4566798297d891b5fae396e93fe4b7003be794e18a194e438a1c802798d0703819
SHAKE128
雜湊值:42a52efbca7de46de5ab54b443870c48
SHAKE256
雜湊值06c9b7ff87b0d9360f0a2e0d2fe58757945f79b8d7b5e7a2a14827c8d37ff570
這些變體提供了不同級別的安全性和輸出長度,以滿足各種加密需求。上述雜湊值是使用不同的 SHA-3 變體對明文“Tutorialspoint”進行的唯一表示。
此外,還有 SHAKE128 和 SHAKE256,它們允許任意長度的輸出,這使得它們適用於需要靈活雜湊長度的應用程式。
各種 SHA 函式的比較
| 函式 | 輸出大小 | 安全性 | 用途 |
|---|---|---|---|
| SHA-1 | 160 位 | 容易受到碰撞攻擊,不再被認為是安全的 | 遺留系統,但應避免在新設計中使用 |
| SHA-2(SHA-224、SHA-256、SHA-384、SHA-512) | 分別為 224、256、384 和 512 位 | 通常被認為是安全的,並且能夠抵抗碰撞攻擊 | 資料完整性驗證、數字簽名、加密應用 |
| SHA-3(SHA3-224、SHA3-256、SHA3-384、SHA3-512) | 分別為 224、256、384 和 512 位 | 旨在提供針對已知加密攻擊的安全保障 | SHA-2 的替代方案,需要加密雜湊的新設計 |
| SHAKE128 和 SHAKE256 | 可變(可以生成任何所需長度的雜湊值) | 旨在提供與 SHA-3 類似的安全保障 | 需要靈活的雜湊長度,加密協議需要動態雜湊長度 |
使用 Python 實現 SHA-3
Python 程式碼計算給定訊息在各種雜湊長度(224、256、384 和 512 位)下的 SHA-3 雜湊值。因此,我們將使用 Python 的 hashlib 包,該包提供安全的雜湊和訊息摘要方法。它包含各種加密雜湊方法的實現,例如 SHA-3。它檢查長度是否為 224、256、384 或 512 位,然後使用正確的 hashlib.sha3_224()、hashlib.sha3_256()、hashlib.sha3_384() 或 hashlib.sha3_512() 函式計算雜湊值。因此,各種 SHA-3 變體的 Python 程式碼如下所示:
import hashlib
def sha3(message, length):
if length == 224:
return hashlib.sha3_224(message.encode()).hexdigest()
elif length == 256:
return hashlib.sha3_256(message.encode()).hexdigest()
elif length == 384:
return hashlib.sha3_384(message.encode()).hexdigest()
elif length == 512:
return hashlib.sha3_512(message.encode()).hexdigest()
else:
return "Invalid length"
message = "Tutorialspoint"
print("SHA3-224 hash:", sha3(message, 224))
print("SHA3-256 hash:", sha3(message, 256))
print("SHA3-384 hash:", sha3(message, 384))
print("SHA3-512 hash:", sha3(message, 512))
輸出
SHA3-224 hash: b3b059b134b17b4bed361b16392b40b16648695eabbf87896c0f8e50 SHA3-256 hash: a789f0a2eb3b13ec69245210b8c522bbb7c33ccb0561729697294bcd35367622 SHA3-384 hash: 68ccee414159dc755f8aa17d82bd1958c956cd09ecf9a221b661c93ce7b36e40237cbadddf48a0600e1eda4ecdd87295 SHA3-512 hash: fb3e821c3a16c720f1137673c6d4247f26e88889093831cf4ca2bb1ef7e0ce4566798297d891b5fae396e93fe4b7003be794e18a194e438a1c802798d0703819
使用 Java 實現 SHA-3
為了實現 SHA-3 變體,我們將使用 Java 上的內建類 - java.security.MessageDigest 和 java.security.NoSuchAlgorithmException。MessageDigest 類用於加密雜湊函式。它提供了 SHA-3 等演算法以進行安全雜湊。程式碼展示瞭如何使用 Java 的 MessageDigest 類計算給定不同長度訊息的 SHA-3 雜湊值。它將雜湊位元組更改為十六進位制表示形式。因此,Java 中 SHA-3 的程式碼如下所示:
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
public class Sha3Algorithm {
public static String sha3(String msg, int length) throws NoSuchAlgorithmException {
MessageDigest digest = MessageDigest.getInstance("SHA3-" + length);
byte[] hashBytes = digest.digest(msg.getBytes());
StringBuilder hexString = new StringBuilder();
for (byte hashByte : hashBytes) {
String hex = Integer.toHexString(0xff & hashByte);
if (hex.length() == 1) hexString.append('0');
hexString.append(hex);
}
return hexString.toString();
}
public static void main(String[] args) throws NoSuchAlgorithmException {
String msg = "Tutorialspoint";
System.out.println("SHA3-224 hash: " + sha3(msg, 224));
System.out.println("SHA3-256 hash: " + sha3(msg, 256));
System.out.println("SHA3-384 hash: " + sha3(msg, 384));
System.out.println("SHA3-512 hash: " + sha3(msg, 512));
}
}
輸出
SHA3-224 hash: b3b059b134b17b4bed361b16392b40b16648695eabbf87896c0f8e50 SHA3-256 hash: a789f0a2eb3b13ec69245210b8c522bbb7c33ccb0561729697294bcd35367622 SHA3-384 hash: 68ccee414159dc755f8aa17d82bd1958c956cd09ecf9a221b661c93ce7b36e40237cbadddf48a0600e1eda4ecdd87295 SHA3-512 hash: fb3e821c3a16c720f1137673c6d4247f26e88889093831cf4ca2bb1ef7e0ce4566798297d891b5fae396e93fe4b7003be794e18a194e438a1c802798d0703819