
- 密碼學教程
- 密碼學 - 首頁
- 密碼學 - 起源
- 密碼學 - 歷史
- 密碼學 - 原理
- 密碼學 - 應用
- 密碼學 - 優點與缺點
- 密碼學 - 現代
- 密碼學 - 傳統密碼
- 密碼學 - 加密的需求
- 密碼學 - 雙重強度加密
- 密碼系統
- 密碼系統
- 密碼系統 - 元件
- 密碼系統攻擊
- 密碼系統 - 彩虹表攻擊
- 密碼系統 - 字典攻擊
- 密碼系統 - 暴力攻擊
- 密碼系統 - 密碼分析技術
- 密碼學型別
- 密碼系統 - 型別
- 公鑰加密
- 現代對稱金鑰加密
- 密碼學雜湊函式
- 金鑰管理
- 密碼系統 - 金鑰生成
- 密碼系統 - 金鑰儲存
- 密碼系統 - 金鑰分發
- 密碼系統 - 金鑰撤銷
- 分組密碼
- 密碼系統 - 流密碼
- 密碼學 - 分組密碼
- 密碼學 - Feistel 分組密碼
- 分組密碼操作模式
- 分組密碼操作模式
- 電子密碼本 (ECB) 模式
- 密碼分組連結 (CBC) 模式
- 密碼反饋 (CFB) 模式
- 輸出反饋 (OFB) 模式
- 計數器 (CTR) 模式
- 經典密碼
- 密碼學 - 反向密碼
- 密碼學 - 凱撒密碼
- 密碼學 - ROT13 演算法
- 密碼學 - 換位密碼
- 密碼學 - 加密換位密碼
- 密碼學 - 解密換位密碼
- 密碼學 - 乘法密碼
- 密碼學 - 仿射密碼
- 密碼學 - 簡單替換密碼
- 密碼學 - 簡單替換密碼加密
- 密碼學 - 簡單替換密碼解密
- 密碼學 - 維吉尼亞密碼
- 密碼學 - 實現維吉尼亞密碼
- 現代密碼
- Base64 編碼和解碼
- 密碼學 - XOR 加密
- 替換技術
- 密碼學 - 單表替換密碼
- 密碼學 - 破解單表替換密碼
- 密碼學 - 多表替換密碼
- 密碼學 - Playfair 密碼
- 密碼學 - 希爾密碼
- 多表替換密碼
- 密碼學 - 一次性密碼本密碼
- 一次性密碼本密碼的實現
- 密碼學 - 轉置技術
- 密碼學 - 柵欄密碼
- 密碼學 - 列置換密碼
- 密碼學 - 密碼隱寫術
- 對稱演算法
- 密碼學 - 資料加密
- 密碼學 - 加密演算法
- 密碼學 - 資料加密標準
- 密碼學 - 三重DES
- 密碼學 - 雙重DES
- 高階加密標準
- 密碼學 - AES 結構
- 密碼學 - AES 變換函式
- 密碼學 - 位元組替換變換
- 密碼學 - 行移位變換
- 密碼學 - 列混合變換
- 密碼學 - 輪金鑰加變換
- 密碼學 - AES 金鑰擴充套件演算法
- 密碼學 - Blowfish 演算法
- 密碼學 - SHA 演算法
- 密碼學 - RC4 演算法
- 密碼學 - Camellia 加密演算法
- 密碼學 - ChaCha20 加密演算法
- 密碼學 - CAST5 加密演算法
- 密碼學 - SEED 加密演算法
- 密碼學 - SM4 加密演算法
- IDEA - 國際資料加密演算法
- 公鑰(非對稱)密碼學演算法
- 密碼學 - RSA 演算法
- 密碼學 - RSA 加密
- 密碼學 - RSA 解密
- 密碼學 - 建立 RSA 金鑰
- 密碼學 - 破解 RSA 密碼
- 密碼學 - ECDSA 演算法
- 密碼學 - DSA 演算法
- 密碼學 - Diffie-Hellman 演算法
- 密碼學中的資料完整性
- 密碼學中的資料完整性
- 訊息認證
- 密碼學數字簽名
- 公鑰基礎設施
- 雜湊
- MD5(訊息摘要演算法 5)
- SHA-1(安全雜湊演算法 1)
- SHA-256(安全雜湊演算法 256 位)
- SHA-512(安全雜湊演算法 512 位)
- SHA-3(安全雜湊演算法 3)
- 雜湊密碼
- Bcrypt 雜湊模組
- 現代密碼學
- 量子密碼學
- 後量子密碼學
- 密碼學協議
- 密碼學 - SSL/TLS 協議
- 密碼學 - SSH 協議
- 密碼學 - IPsec 協議
- 密碼學 - PGP 協議
- 影像和檔案加密
- 密碼學 - 影像
- 密碼學 - 檔案
- 密碼隱寫術 - 影像
- 檔案加密和解密
- 密碼學 - 檔案加密
- 密碼學 - 檔案解密
- 物聯網中的密碼學
- 物聯網安全挑戰、威脅和攻擊
- 物聯網安全的加密技術
- 物聯網裝置的通訊協議
- 常用加密技術
- 自定義構建加密演算法(混合加密)
- 雲加密
- 量子密碼學
- 密碼學中的影像隱寫術
- DNA 密碼學
- 密碼學中的一次性密碼 (OTP) 演算法
- 區別
- 密碼學 - MD5 與 SHA1
- 密碼學 - RSA 與 DSA
- 密碼學 - RSA 與 Diffie-Hellman
- 密碼學與密碼學
- 密碼學 - 密碼學與密碼分析
- 密碼學 - 經典與量子
- 密碼學與隱寫術
- 密碼學與加密
- 密碼學與網路安全
- 密碼學 - 流密碼與分組密碼
- 密碼學 - AES 與 DES 密碼
- 密碼學 - 對稱與非對稱
- 密碼學有用資源
- 密碼學 - 快速指南
- 密碼學 - 討論
密碼學 - 轉置技術
轉置技術是一種加密方法,它透過對給定的明文進行置換來工作。轉置密碼是透過使用轉置技術將普通文字對映到密文而建立的。
本章將涵蓋轉置技術的多種用途,以及轉置和替換技術之間的差異。
另一方面,替換方法用密文中的符號替換明文中的符號。但是,轉置方法透過對原始明文應用置換來生成密文。
轉置技術
柵欄轉置
列置換
列置換 - 多輪
書籍密碼/執行金鑰密碼
維爾南密碼
讓我們在下面的部分中逐一討論這些技術 -
柵欄轉置
柵欄是一種基本的轉置方法,其中明文寫成一系列對角線,然後逐行讀取以生成密文。
演算法
步驟 1:使用一系列對角線來編寫明文。
步驟 2:然後將文字作為一系列行讀取,以提取密文。
為了幫助您理解它,讓我舉一個例子。
明文:讓我們今天見面
我們現在將這個簡單的句子以對角線格式編寫,如下所示,遵循特定的順序 -
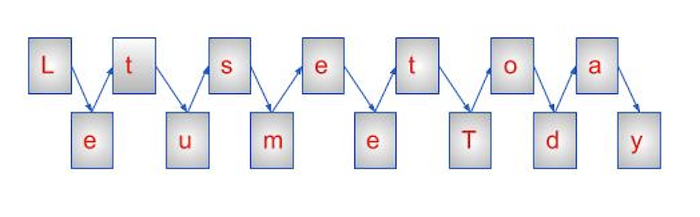
透過檢視影像,我們可以看到為什麼它被稱為“柵欄”,它實際上看起來像一個柵欄。
將訊息寫成一系列對角線後,必須將其作為一系列行讀取以提取密文。因此,在讀取第一行後,密文的前半部分將為 -
Ltsetoa
我們將透過讀取柵欄的第二行來解密密文的第二部分 -
eumeTdy
現在,我們將密文的兩個部分加在一起以獲得完整的密文,如下所示 -
密文:LTSETOAEUMETDY
柵欄密碼易於使用,對於密碼分析師來說,破解起來也更容易。因此,需要一種更復雜的方法。
列置換
與柵欄相比,列置換密碼更加複雜。要使用此方法獲取密文,請使用以下步驟 -
演算法
步驟 1:明文以逐行的方式寫入給定大小的矩形矩陣中。
步驟 2:要獲取密文,請逐列讀取矩形矩陣中的文字。但是,在逐列讀取資料之前,必須先置換列的順序。接收到的訊息是密文訊息。
要了解列置換,請考慮以下示例 -
明文:讓我們今天見面
將明文放置在一個預定義大小的矩形中。在我們的例子中,矩形的定義大小為 3x5。下圖顯示了放置在 3x5 矩形中的明文。此外,我們還置換了列的順序。
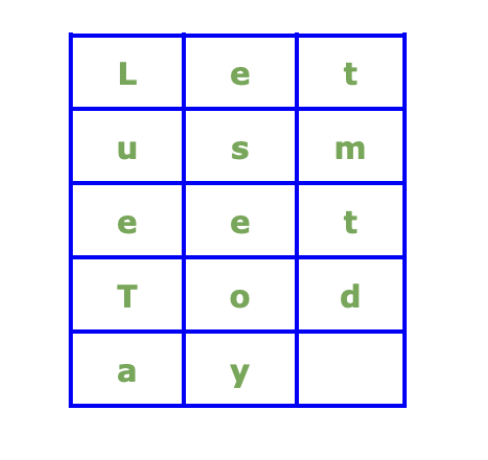
要獲取密文,我們需要以置換後的列順序逐列讀取明文。因此,使用列置換密碼建立的密文如下 -
密文:LUETAESEOYEMTD
與柵欄密碼類似,列置換密碼也很容易破解。密碼分析師只需要測試列順序的一些排列和組合,即可獲得導致原始訊息的置換列順序。因此,必須使用更復雜的方法來確保加密的安全性。
列置換 - 多輪/改進的列置換
它與簡單的列置換方法相同,但提供了一些改進。此列置換方法對明文應用多次。使用多輪列置換方法的步驟如下 -
演算法
步驟 1:明文以逐行的方式寫入預定義的矩形中。
步驟 2:要獲取密文,請逐列讀取矩形中的明文。在逐列讀取矩形中的文字之前,請以與基本列置換技術相同的方式重新排列列。
步驟 3:重複上述步驟多次以生成最終密文。
因此,現在我們將根據上述方法執行第一輪,第一輪後的密文將如下所示 -
密文:LUETAESEOYEMTD
要解密第二輪的密文,請將第一輪的密文排列在一個 3x5 的矩形中並重新排列列。提取的第二輪密文為 LSYETMOATTEMUD。在此方法中,我們可以根據需要執行任意次數的迭代。增加重複次數會增加複雜度。
書籍密碼/執行金鑰密碼
書籍密碼,也稱為執行金鑰密碼,其操作基本原理與一次性密碼本密碼相同。在一次性密碼本密碼中,金鑰與明文長度相同,並在使用後刪除。每次使用新金鑰傳送新訊息。
金鑰或一次性密碼本是從書籍中提取的,這比書籍密碼中的一次性密碼有所改進。讓我們概述一下各個階段 -
步驟 1:將明文轉換為數字形式:A=0,B=1,C=3,...Z=25。
步驟 2:從任何書籍中獲取一次性密碼本或金鑰,並將其轉換為數字格式。但金鑰必須與明文長度相同。
步驟 3:現在組合明文和金鑰的數字形式,將每個明文字母與相應的金鑰文字字母匹配。如果任何明文字母與匹配的金鑰文字字母的總和超過 26,則減去 26。
讓我們用一個例子來討論一下 -
明文:明天見面。
金鑰來自書籍:ANENCRYPTION。
現在我們必須將此明文和金鑰文字轉換為數字形式,並將它們組合起來以獲得密文,如下面的影像所示 -
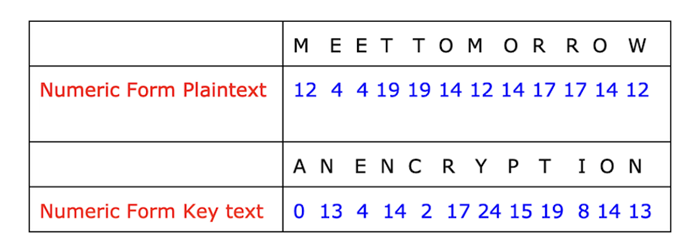
新增明文和金鑰文字的數字形式。因此,在新增這兩個值後,我們將得到 12 7 8 32 21 31 36 29 36 25 28 35 -
現在我們在上面的結果中得到了一些數字(以粗體顯示),這些數字大於 26,所以我們將這些數字減去 26,最終結果將是 − 12 17 8 6 21 5 10 3 10 25 3 9。
因此,新的密文將是:MRIGVFKDKZDJ。
維爾南密碼
一次性密碼本是維爾南密碼的一個子集,它使用一組隨機的、不重複的字元作為其輸入密文。用於轉置的密文在使用後永遠不會用於其他訊息。輸入密文的長度需要與明文的長度匹配。
演算法
步驟 1:將明文中的每個字元按數字順序排列,例如 A = 0,B = 1,... Z = 25。
步驟 2:對輸入密文中的每個字元再次執行步驟 1。
步驟 3:對於每個等效於明文字元的數字,將相應的輸入密文字元數字加 1。
步驟 4:如果總和大於 25,則從中減去 26。
步驟 5:將每個和的數字轉換為相應的字元。
步驟 6:步驟 5 的輸出將成為密文。
維爾南密碼僅適用於簡短的訊息,因為在使用後,輸入密文不能再次使用。
例如:明文訊息是 point,密文是 ntcba
| 明文 | p | o | i | n | t |
|---|---|---|---|---|---|
| 15 | 14 | 8 | 13 | 19 | |
| 內部密文 | n | t | c | b | a |
| 13 | 19 | 2 | 1 | 0 | |
| 明文和輸入密文的加法 | 27 | 33 | 10 | 14 | 19 |
| 如果大於 26,則減去 26 | 1 | 6 | 10 | 14 | 19 |
| 密文 | b | g | k | o | t |
因此,密文將是:bgkot。
所以,這就是關於轉置技術的全部內容,它使用置換將明文轉換為密文。