SHA-1（安全雜湊演算法1）

SHA-1是一種密碼雜湊函式，它可以從任何長度不超過2⁶⁴ - 1位的輸入訊息生成一個160位的雜湊值（也稱為訊息摘要）。

SHA-1是由國家安全域性（NSA）設計的，並於1995年由國家標準與技術研究院（NIST）作為安全雜湊標準（SHS）的一部分發布。

SHA-1是單向函式，這意味著無法從其雜湊值計算出原始訊息。

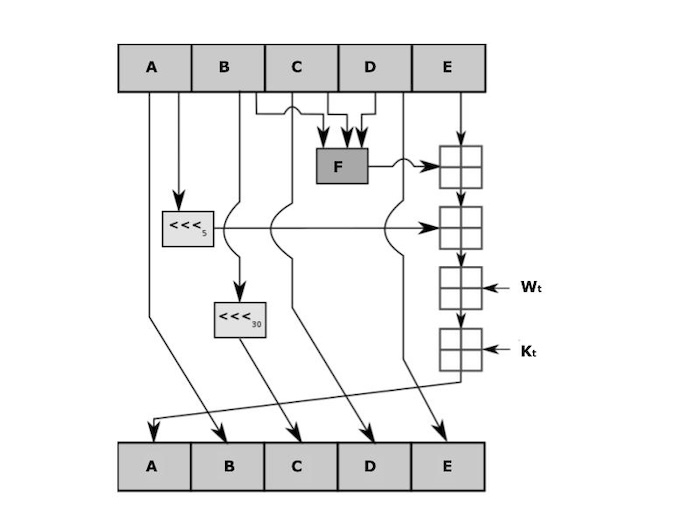
在上圖中，在SHA-1壓縮函式的一個迴圈中，A、B、C、D和E代表32位狀態字。

F = 變化的非線性函式。
⋘n = 左移n位。
n = 每個操作的值都不同。
W_t = 第t輪的擴充套件訊息字；
K_t = 第t輪的輪常數；以及
⊞ = 模2³²加法。

演算法

以下是SHA-1中需要遵循的步驟：

初始化
- 讓我們從一些初始值開始。
- 用正確的值設定所有五個變數（h0到h4）。
預處理
- 準備要進行雜湊處理的訊息。
- 應在訊息的末尾新增一個'1'位。
- 為了設定訊息的最大長度，請追加一些'0'位。
- 在訊息的末尾，包含訊息的原始長度（以位為單位）。
處理
- 將訊息分成易於管理的部分，並分別處理每一部分。
- 每一部分應包含512位。
- 將這些部分分別分成十六個32位字。
- 使用公式將這些字擴充套件成八十個32位字。
主迴圈
- 遍歷每個字並進行一些計算。
- 根據字的位置和值，更新臨時變數。
- 根據這些計算，更新雜湊值。
最終化
- 要獲得最終雜湊值，請組合雜湊值。
- 使用預定的順序排列雜湊值以生成一個160位整數。

SHA-1的實現

以下是SHA-1演算法的Python和Java實現，以及結果：

使用Python

此Python程式碼透過使用hashlib包實現SHA-1演算法。它定義了函式sha1，該函式接受訊息作為輸入並輸出使用SHA-1生成的雜湊值。在函式內部，生成一個SHA-1雜湊物件並使用輸入訊息對其進行更新，並返回雜湊的十六進位制摘要。

import hashlib

def sha1(message):
   # generate a SHA-1 hash object
   sha1_hash = hashlib.sha1()

   # update the hash object 
   sha1_hash.update(message.encode('utf-8'))

   # hexadecimal digest of the hash
   return sha1_hash.hexdigest()

# execute the function
message = "Hello, everyone!"
sha1_hash = sha1(message)
print("SHA-1 hash:", sha1_hash)

輸出

SHA-1 hash: 9a8bfaaace7b9e422f79ef862956e3512aa9d8ea

使用Java

在此Java程式碼中，我們將使用java.security.MessageDigest類。該類實現了SHA-1演算法。它定義了一個名為sha1的方法，該方法接受訊息作為輸入並返回其SHA-1雜湊值。該函式為SHA-1建立一個MessageDigest物件，用訊息位元組更新它，獲取摘要位元組。因此，請參考下面的Java程式碼以獲取SHA-1：

import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;

public class SHA1 {
   public static String sha1(String message) {
      try {
         // generate a MessageDigest object here
         MessageDigest md = MessageDigest.getInstance("SHA-1");

         // then update the digest
         md.update(message.getBytes());

         // the digest bytes
         byte[] digestBytes = md.digest();

         // change the bytes to hexadecimal
         StringBuilder sb = new StringBuilder();
         for (byte b : digestBytes) {
            sb.append(String.format("%02x", b));
         }

         return sb.toString();
      } catch (NoSuchAlgorithmException e) {
         e.printStackTrace();
         return null;
      }
   }

   public static void main(String[] args) {
      // execute the function
      String message = "Hello, tutorialspoint!";
      String sha1Hash = sha1(message);
      System.out.println("SHA-1 hash: " + sha1Hash);
   }
}

輸出

SHA-1 hash: 92c2164b880f6a60355a0764dd59ae828b53d6f3

SHA-1的特性

SHA-1具有幾個特性，使其適合各種應用：

雜湊函式的基本目的是為每個輸入訊息生成不同的雜湊值。SHA-1確保兩個不同的訊息不太可能生成相同的雜湊結果，從而使其能夠抵抗碰撞攻擊。
SHA-1是單向函式，這意味著無法從其雜湊值檢索原始訊息。此屬性對於數字簽名、密碼儲存和其他安全相關應用至關重要。
SHA-1具有固定的160位輸出長度，無論輸入訊息的大小如何。這允許您輕鬆比較雜湊值並將它們儲存在資料庫中。

SHA-1的應用

SHA-1用於各種應用，例如：

數字簽名 - 數字簽名演算法（如數字簽名標準 (DSS)）使用SHA-1來確保資料完整性和不可否認性。
密碼儲存 - 密碼使用SHA-1儲存在資料庫中。系統儲存密碼的雜湊值而不是實際密碼，這使得攻擊者難以竊取密碼。
安全通訊 - SHA-1在安全通訊協議（如傳輸層安全 (TLS) 和安全套接字層 (SSL)）中保護資料完整性和機密性。

SHA-1的漏洞

雖然 SHA-1 之前被認為是一種安全的雜湊演算法，但目前它容易受到各種攻擊。

SHA-1 的根本風險在於其抗碰撞性，這意味著兩個不同的訊息可以生成相同的雜湊值。這可以用於多種方式，例如：

生日攻擊 − 生日攻擊是一種碰撞攻擊，攻擊者試圖找到兩個具有相同雜湊值的獨立訊息。使用 SHA-1 的生日攻擊只需要 2⁸⁰ 次計算，對於現代計算能力來說是可行的。
中間人攻擊 − 中間人攻擊發生在攻擊者攔截並修改雙方之間傳送的資料時。SHA-1 允許攻擊者生成一個與原始訊息具有相同雜湊值的修改後的訊息，這使得難以檢測到更改。
證書偽造 − 數字證書使用 SHA-1 來驗證網站或服務的真實性。但是，由於容易受到碰撞攻擊，攻擊者可以生成一個與真實證書具有相同雜湊值的偽造證書。

SHA-1 的替代方案

由於 SHA-1 的弱點，建議採用更強大的雜湊演算法，例如 SHA-2 和 SHA-3。
SHA-2 是一組雜湊演算法，其中包含 SHA-256、SHA-384 和 SHA-512，它們分別生成 256、384 和 512 位的雜湊值。
SHA-2 是為了取代 SHA-1 而建立的，被認為更加安全。SHA-3 是 NIST 於 2012 年開發的一種較新的雜湊函式，其建立雜湊值的方式與 SHA-2 不同。

最佳實踐

由於 SHA-1 容易受到攻擊，一些舊程式和系統仍在使用它。為了最大限度地降低此類情況下的攻擊風險，務必遵循最佳實踐：

避免將 SHA-1 應用於新的應用程式和平臺 − 選擇更強大的雜湊演算法，例如 SHA-2 和 SHA-3。
升級舊系統 − 如果你在舊系統中繼續使用 SHA-1，建議儘快切換到更好的雜湊演算法。
使用加鹽雜湊 − 為了提高密碼儲存安全性，加鹽雜湊在雜湊後向密碼新增隨機文字（鹽）。這使得攻擊者使用預計算雜湊表破解密碼變得更加困難。

列印頁面