密碼學速成指南

密碼學的起源

從古至今，人類始終存在著兩種內在需求：(a) 交流和分享資訊；(b) 選擇性地交流資訊。這兩種需求催生了對資訊進行編碼的藝術，只有預期的接收者才能訪問這些資訊。即使被加密的訊息落入未授權者手中，他們也無法提取任何資訊。

隱藏資訊以在資訊安全中引入保密性的藝術和科學被稱為密碼學。

“密碼學”一詞是由兩個希臘詞組合而成的，“Krypto”意為隱藏，“graphene”意為書寫。

密碼學歷史

密碼學的藝術被認為是隨著書寫藝術而誕生的。隨著文明的發展，人類組織成部落、群體和王國。這導致了權力、戰爭、霸權和政治等觀念的出現。這些觀念進一步激發了人們秘密與特定接收者交流的自然需求，這反過來又確保了密碼學的持續發展。

密碼學的根源可以追溯到羅馬和埃及文明。

象形文字——最古老的密碼技術

密碼學最早的已知證據可以追溯到“象形文字”的使用。大約4000年前，埃及人使用象形文字書寫的訊息進行交流。這種密碼只有代表國王傳遞資訊的抄寫員才知道。下面顯示了一個這樣的象形文字。

後來，學者們在公元前500年到600年期間開始使用簡單的單字母替換密碼。這涉及到根據某種秘密規則用其他字母替換訊息中的字母。這個**規則**變成了檢索從亂碼訊息中檢索回訊息的**金鑰**。

早期的羅馬密碼方法，俗稱**凱撒移位密碼**，依賴於將訊息的字母按商定的數字進行移位（3是一個常見的選擇），該訊息的接收者然後將字母按相同的數字移回，並獲得原始訊息。

隱寫術

隱寫術類似，但為密碼學增加了另一個維度。在這種方法中，人們不僅希望透過隱藏資訊來保護資訊的秘密，而且還希望確保任何未經授權的人都沒有證據表明資訊的存在。例如，**不可見水印**。

在隱寫術中，意外的接收者或入侵者不知道觀察到的資料包含隱藏資訊。在密碼學中，入侵者通常知道正在通訊資料，因為他們可以看到編碼/加密的訊息。

密碼學的發展

在歐洲文藝復興時期及之後，義大利和教皇國推動了密碼技術的迅速發展。在這個時代，人們研究了各種分析和攻擊技術來破解秘密程式碼。

15世紀出現了改進的編碼技術，例如**維吉尼亞編碼**，它提供了在訊息中移動字母的多個可變位置，而不是將它們移動相同數量的位置。
直到19世紀以後，密碼學才從臨時性的加密方法發展成為更復雜的資訊安全藝術和科學。
在20世紀初期，機械和機電機器（例如**Enigma轉子機**）的發明為編碼資訊提供了更先進和有效的方法。
在第二次世界大戰期間，**密碼學**和**密碼分析**都變得極其數學化。

隨著該領域取得的進步，政府組織、軍事單位和一些公司開始採用密碼學的應用。他們使用密碼學來保護他們的秘密免受他人侵犯。現在，計算機和網際網路的出現使普通民眾都能使用有效的密碼學。

現代密碼學

現代密碼學是計算機和通訊安全的基礎。它的基礎是基於數論、計算複雜性理論和機率論等各種數學概念。

現代密碼學的特點

有三個主要特點將現代密碼學與經典方法區分開來。

經典密碼學	現代密碼學
它直接操作傳統字元，即字母和數字。	它在二進位制位序列上執行。
它主要基於“安全性透過模糊性”。採用的編碼技術保密，只有參與通訊的雙方才知道。	它依賴於公開的數學演算法來編碼資訊。透過用作演算法種子的秘密金鑰來獲得保密性。演算法的計算難度、秘密金鑰的缺失等，即使攻擊者知道用於編碼的演算法，也使他無法獲得原始資訊。
它需要整個密碼系統才能進行機密通訊。	現代密碼學只需要對安全通訊感興趣的各方擁有秘密金鑰即可。

密碼學的背景

密碼學，即對密碼系統的研究，可以細分為兩個分支：

密碼學
密碼分析

什麼是密碼學？

密碼學是建立能夠提供資訊安全的密碼系統的藝術和科學。

密碼學處理數字資料的實際安全。它指的是基於提供基本資訊安全服務的數學演算法的設計機制。您可以將密碼學視為包含安全應用程式中不同技術的龐大工具包的建立。

什麼是密碼分析？

破解密文的藝術和科學被稱為密碼分析。

密碼分析是密碼學的姊妹分支，兩者並存。密碼學過程產生用於傳輸或儲存的密文。它涉及對密碼機制的研究，目的是破解它們。密碼分析也用於新密碼技術的安全性設計中，以測試其強度。

注意 − 密碼學關注密碼系統的設計，而密碼分析研究密碼系統的破解。

密碼學的安全服務

使用密碼學的首要目標是提供以下四項基本資訊安全服務。讓我們來看看密碼學旨在實現的目標。

機密性

機密性是密碼學提供的基本安全服務。它是一種防止未授權人員訪問資訊的安全性服務。有時也稱為隱私或保密性。

機密性可以透過多種方式實現，從物理安全到使用數學演算法進行資料加密。

資料完整性

這是一種處理識別資料任何更改的安全服務。資料可能被未授權的實體有意或意外地修改。完整性服務確認資料自上次被授權使用者建立、傳輸或儲存以來是否保持完整。

資料完整性無法防止資料被更改，但提供了一種檢測資料是否被未授權方式操縱的方法。

身份驗證

身份驗證提供發件人的身份識別。它向接收方確認收到的資料僅由已識別和驗證的發件人傳送。

身份驗證服務有兩個變體：

訊息認證識別訊息的發起者，而不管傳送訊息的路由器或系統。
實體認證是確保資料來自特定實體（例如特定網站）的保證。

除了發件人之外，身份驗證還可以提供關於資料的其他引數的保證，例如建立/傳輸的日期和時間。

不可否認性

這是一種確保實體無法拒絕先前承諾或行為所有權的安全服務。它保證資料的原始建立者不能否認已將所述資料建立或傳輸給接收者或第三方。

不可否認性是在可能發生資料交換爭議的情況下最理想的屬性。例如，一旦電子下單，如果在此交易中啟用了不可否認性服務，則購買者無法否認採購訂單。

密碼學原語

密碼學原語只不過是密碼學中的工具和技術，可以選擇性地使用它們來提供一組所需的安全服務：

加密
雜湊函式
訊息認證碼 (MAC)
數字簽名

下表顯示了可以獨立實現特定安全服務的原語。

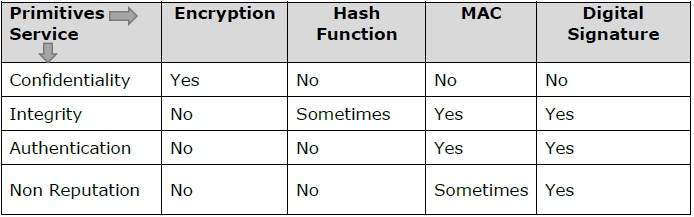
注意 − 密碼學原語彼此錯綜複雜地關聯，通常會將它們組合起來以從密碼系統中獲得一組所需的安全服務。

密碼系統

密碼系統是密碼技術的實現及其配套的基礎設施，用於提供資訊安全服務。密碼系統也稱為密碼系統。

讓我們討論一個簡單的密碼系統模型，該模型為正在傳輸的資訊提供機密性。該基本模型如下圖所示：

該圖顯示了一個傳送方，他希望以任何攔截或竊聽通訊通道的一方都無法提取資料的方式將一些敏感資料傳輸給接收方。

這個簡單密碼系統的目標是，在流程結束時，只有傳送方和接收方才能知道明文。

密碼系統的組成部分

基本密碼系統的各個組成部分如下：

明文。這是在傳輸過程中需要保護的資料。
加密演算法。這是一個數學過程，它為任何給定的明文和加密金鑰生成密文。它是一種密碼演算法，它以明文和加密金鑰作為輸入，併產生密文。
密文。這是加密演算法使用特定加密金鑰生成的明文的混淆版本。密文不受保護。它在公共通道上傳輸。任何可以訪問通訊通道的人都可以攔截或破壞它。
解密演算法，這是一個數學過程，它為任何給定的密文和解密金鑰生成唯一的明文。它是一種密碼演算法，它以密文和解密金鑰作為輸入，並輸出明文。解密演算法本質上是反轉加密演算法，因此與之密切相關。
加密金鑰。這是傳送方已知的值。傳送方將加密金鑰與明文一起輸入加密演算法以計算密文。
解密金鑰。這是接收方已知的值。解密金鑰與加密金鑰相關，但不總是與之相同。接收方將解密金鑰與密文一起輸入解密演算法以計算明文。

對於給定的密碼系統，所有可能的解密金鑰的集合稱為金鑰空間。

攔截者（攻擊者）是試圖確定明文的未授權實體。他可以看到密文，並且可能知道解密演算法。但是，他絕不能知道解密金鑰。

密碼系統的型別

從根本上說，根據系統中執行加密-解密的方式，密碼系統有兩種型別：

對稱金鑰加密
非對稱金鑰加密

這些密碼系統之間的主要區別在於加密金鑰和解密金鑰之間的關係。從邏輯上講，在任何密碼系統中，兩個金鑰都密切相關。使用與加密金鑰無關的金鑰來解密密文實際上是不可能的。

對稱金鑰加密

使用相同的金鑰加密和解密資訊的加密過程稱為對稱金鑰加密。

對稱密碼系統研究被稱為對稱密碼學。對稱密碼系統有時也稱為秘密金鑰密碼系統。

一些眾所周知的對稱金鑰加密方法包括：數字加密標準 (DES)、三重 DES (3DES)、IDEA 和 BLOWFISH。

在 1970 年之前，所有密碼系統都採用對稱金鑰加密。即使在今天，它的相關性也非常高，並且在許多密碼系統中被廣泛使用。這種加密不太可能消失，因為它比非對稱金鑰加密具有一定的優勢。

基於對稱金鑰加密的密碼系統的顯著特徵是：

使用對稱金鑰加密的人員必須在交換資訊之前共享一個共同的金鑰。
建議定期更改金鑰以防止對系統進行任何攻擊。
需要存在一個強大的機制來交換通訊雙方之間的金鑰。由於需要定期更改金鑰，因此此機制變得昂貴且繁瑣。
在一組n人中，要啟用任意兩人之間的雙向通訊，該組所需的金鑰數量為n × (n – 1)/2。
此加密中的金鑰長度（位數）較小，因此加密-解密過程比非對稱金鑰加密快。
執行對稱演算法所需的計算機系統處理能力較低。

對稱金鑰密碼系統的挑戰

使用對稱金鑰密碼學有兩個限制性挑戰。

金鑰建立 − 在任何通訊之前，傳送方和接收方都需要就一個秘密對稱金鑰達成一致。它需要一個安全的金鑰建立機制。
信任問題 − 由於傳送方和接收方使用相同的對稱金鑰，因此隱含地要求傳送方和接收方“相互信任”。例如，接收方可能已將金鑰丟失給攻擊者，而傳送方未被告知。

這兩個挑戰對於現代通訊來說是極大的限制。如今，人們需要與不熟悉且不可信的各方交換資訊。例如，線上賣家和客戶之間的溝通。對稱金鑰加密的這些限制導致了非對稱金鑰加密方案的出現。

非對稱金鑰加密

使用不同的金鑰加密和解密資訊的加密過程稱為非對稱金鑰加密。儘管金鑰不同，但它們在數學上是相關的，因此，透過解密密文來檢索明文是可行的。該過程如下圖所示：

非對稱金鑰加密是在 20 世紀發明的，以克服通訊人員之間預共享秘密金鑰的必要性。該加密方案的顯著特徵如下：

此係統中的每個使用者都需要有一對不同的金鑰，私鑰和公鑰。這些金鑰在數學上是相關的——當使用一個金鑰進行加密時，另一個金鑰可以將密文解密回原始明文。
它需要將公鑰放入公共儲存庫，並將私鑰作為受保護的秘密。因此，這種加密方案也稱為公鑰加密。
儘管使用者的公鑰和私鑰相關，但在計算上並不容易從一個金鑰找到另一個金鑰。這是此方案的優勢。
當主機1需要向主機2傳送資料時，他從儲存庫中獲取主機2的公鑰，加密資料並傳輸。
主機2使用他的私鑰提取明文。
此加密中的金鑰長度（位數）很大，因此加密-解密過程比對稱金鑰加密慢。
執行非對稱演算法所需的計算機系統處理能力更高。

對稱密碼系統是一個自然的概念。相反，公鑰密碼系統很難理解。

您可能會想，加密金鑰和解密金鑰如何“相關”，但又不可能根據加密金鑰確定解密金鑰？答案在於數學概念。可以設計一個具有此屬性的密碼系統。公鑰密碼學的概念相對較新。已知的公鑰演算法比對稱演算法少。

公鑰密碼系統的挑戰

公鑰密碼系統面臨一個重大挑戰——使用者需要相信他與某人通訊時使用的公鑰確實是該人的公鑰，並且沒有被惡意第三方欺騙。

這通常透過由可信第三方組成的公鑰基礎設施 (PKI) 來實現。第三方安全地管理並證明公鑰的真實性。當請求第三方提供任何通訊者 X 的公鑰時，人們相信他們會提供正確的公鑰。

第三方透過證明、公證或其他一些過程來驗證使用者身份——X 是唯一且全域性唯一的 X。使已驗證的公鑰可用的最常見方法是將它們嵌入到由可信第三方數字簽名的證書中。

加密方案之間的關係

以下是兩種型別的密碼系統的基本金鑰屬性的摘要：

	對稱密碼系統	公鑰密碼系統
金鑰之間的關係	相同	不同，但數學上相關
加密金鑰	對稱的	公開的
解密金鑰	對稱的	私有的

由於兩種系統的優缺點，對稱金鑰和公鑰密碼系統經常在實際的資訊安全系統中一起使用。

Kerckhoffs 密碼系統原理

19 世紀，荷蘭密碼學家 A. Kerckhoffs 提供了良好密碼系統的要求。Kerckhoffs 指出，即使密碼系統的所有內容（金鑰除外）都是公開的，該系統也應該是安全的。Kerckhoffs 為密碼系統定義的六個設計原則如下：

密碼系統即使在數學上並非如此，也應該實際上牢不可破。
密碼系統落入入侵者手中不應導致系統受到任何損害，從而防止使用者受到任何不便。
金鑰應該易於溝通、記憶和更改。
密文應可以透過電報（不安全的通道）傳輸。
加密裝置和檔案應便於攜帶，並可由一人操作。
最後，系統必須易於使用，既不需要精神壓力，也不需要了解一系列需要遵守的規則。

第二條規則目前被稱為 **Kerckhoffs 原理**。它實際上應用於所有當代加密演算法，例如 DES、AES 等。這些公共演算法被認為是完全安全的。加密訊息的安全完全取決於秘密加密金鑰的安全。

將演算法保密可能會對密碼分析構成重大障礙。然而，只有在嚴格限制的範圍內使用演算法時，才能將演算法保密。

在現代，密碼學需要滿足連線到網際網路的使用者。在這種情況下，使用秘密演算法是不可行的，因此 Kerckhoffs 原理成為現代密碼學中設計算法的基本準則。

對密碼系統的攻擊

在當今時代，不僅商業，幾乎所有人類生活方面都由資訊驅動。因此，保護有用的資訊免受惡意活動（如攻擊）的影響已成為當務之急。讓我們考慮一下資訊通常會受到哪些型別的攻擊。

攻擊通常根據攻擊者執行的操作進行分類。因此，攻擊可以是 **被動的** 或 **主動的**。

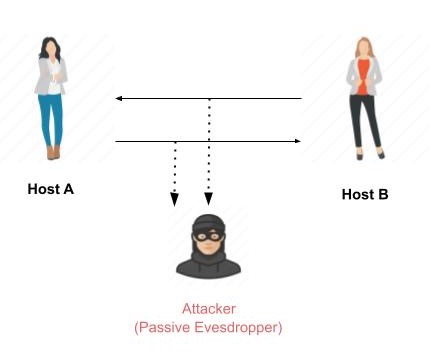
被動攻擊

被動攻擊的主要目標是獲得 **對資訊的未授權訪問**。例如，攔截和竊聽通訊通道等行為可以被視為被動攻擊。

這些行為本質上是被動的，因為它們既不影響資訊也不中斷通訊通道。被動攻擊通常被視為 *竊取* 資訊。竊取實物和竊取資訊的區別在於，竊取資料後，所有者仍然擁有該資料。因此，被動資訊攻擊比竊取貨物更危險，因為資訊竊取可能未被所有者注意到。

主動攻擊

主動攻擊涉及透過對資訊進行某些處理來以某種方式更改資訊。例如：

以未經授權的方式修改資訊。
啟動意外或未經授權的資訊傳輸。
更改身份驗證資料，例如與資訊關聯的發起者姓名或時間戳
未經授權刪除資料。
拒絕合法使用者訪問資訊（拒絕服務）。

密碼學提供了許多工具和技術，用於實現能夠防止上述大多數攻擊的密碼系統。

攻擊者的假設

讓我們看看密碼系統周圍普遍存在的環境，以及用於破壞這些系統的攻擊型別：

密碼系統周圍的環境

在考慮對密碼系統的可能攻擊時，有必要了解密碼系統環境。攻擊者的假設和對環境的瞭解決定了他的能力。

在密碼學中，對安全環境和攻擊者的能力做出以下三個假設。

加密方案的細節

密碼系統的設計基於以下兩種密碼演算法：

**公共演算法**——使用此選項，演算法的所有詳細資訊都屬於公共領域，眾所周知。
**專有演算法**——只有系統設計人員和使用者知道演算法的詳細資訊。

對於專有演算法，安全是透過模糊性來確保的。私有演算法可能不是最強大的演算法，因為它們是在內部開發的，並且可能沒有經過廣泛的弱點調查。

其次，它們只允許封閉組之間的通訊。因此，它們不適用於現代通訊，在現代通訊中，人們與大量已知或未知的實體進行通訊。此外，根據 Kerckhoffs 原理，演算法最好是公開的，加密強度在於 *金鑰*。

因此，關於安全環境的第一個假設是 **攻擊者知道加密演算法**。

密文的可用性

我們知道，一旦明文加密成密文，它就會被放在不安全的公共通道（例如電子郵件）上進行傳輸。因此，攻擊者顯然可以假設它 **可以訪問密碼系統生成的密文**。

明文和密文的可用性

這個假設不像其他假設那麼明顯。但是，在某些情況下，攻擊者可能 **可以訪問明文和相應的密文**。一些可能的這種情況是：

攻擊者影響傳送者轉換他選擇的明文並獲得密文。
接收者可能會無意中向攻擊者洩露明文。攻擊者可以訪問從開放通道收集的相應密文。
在公鑰密碼系統中，加密金鑰處於開放域，任何潛在的攻擊者都知道。使用此金鑰，他可以生成成對的相應明文和密文。

密碼攻擊

攻擊者的基本意圖是破壞密碼系統並從密文中找到明文。要獲得明文，攻擊者只需要找出秘密解密金鑰，因為演算法已經在公共領域。

因此，他將最大努力用於找出密碼系統中使用的秘密金鑰。一旦攻擊者能夠確定金鑰，則被攻擊的系統就被認為是 *被破壞的* 或 *被破壞的*。

根據使用的方法，對密碼系統的攻擊分類如下：

**僅密文攻擊 (COA)**——在這種方法中，攻擊者可以訪問一組密文。他無法訪問相應的明文。當可以從給定的密文集確定相應的明文時，COA 就被認為是成功的。有時，可以從這種攻擊中確定加密金鑰。現代密碼系統可以防止僅密文攻擊。
**已知明文攻擊 (KPA)**——在這種方法中，攻擊者知道密文某些部分的明文。任務是使用此資訊解密密文的其餘部分。這可以透過確定金鑰或透過其他方法來完成。這種攻擊的最佳示例是對分組密碼的 *線性密碼分析*。
**選擇明文攻擊 (CPA)**——在這種方法中，攻擊者有他選擇的文字被加密。因此，他擁有他選擇的密文-明文對。這簡化了他確定加密金鑰的任務。這種攻擊的一個例子是應用於分組密碼和雜湊函式的 *差分密碼分析*。流行的公鑰密碼系統 RSA 也容易受到選擇明文攻擊。
**字典攻擊**——這種攻擊有很多變體，所有這些變體都涉及編譯“字典”。在這種攻擊的最簡單方法中，攻擊者構建了一個包含他一段時間內學習到的密文和相應明文的字典。將來，當攻擊者獲得密文時，他將參考字典以查詢相應的明文。
**暴力攻擊 (BFA)**——在這種方法中，攻擊者試圖透過嘗試所有可能的金鑰來確定金鑰。如果金鑰是 8 位長的，則可能的金鑰數量為 2⁸ = 256。攻擊者知道密文和演算法，現在他逐一嘗試所有 256 個金鑰進行解密。如果金鑰很長，則完成攻擊所需的時間將非常長。
**生日攻擊**——這種攻擊是暴力技術的變體。它用於對抗密碼雜湊函式。當詢問班上的學生他們的生日時，答案是可能的 365 個日期之一。讓我們假設第一個學生的生日是 8 月 3 日。然後，要找到下一個生日是 8 月 3 日的學生，我們需要詢問大約 1.25 * √365 ≈ 25 個學生。

類似地，如果雜湊函式產生 64 位雜湊值，則可能的雜湊值是 1.8x10¹⁹。透過對不同輸入重複評估函式，預計在大約 5.1x10⁹ 個隨機輸入後將獲得相同的輸出。

如果攻擊者能夠找到兩個產生相同雜湊值的不同的輸入，則這是一個 **衝突**，並且該雜湊函式被認為是被破壞的。
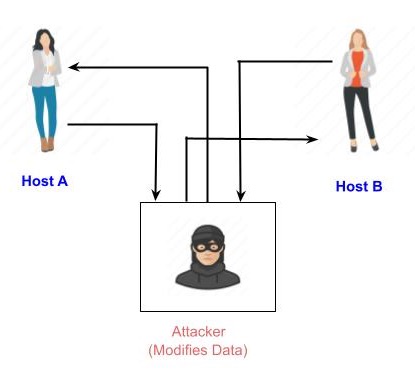
**中間人攻擊 (MIM)**——這種攻擊的目標主要是涉及金鑰交換的公鑰密碼系統，在通訊發生之前進行金鑰交換。
- 主機 *A* 想要與主機 *B* 通訊，因此請求 *B* 的公鑰。
- 攻擊者攔截此請求併發送他的公鑰。
- 因此，主機 *A* 傳送給主機 *B* 的任何內容，攻擊者都可以讀取。
- 為了保持通訊，攻擊者在讀取後使用他的公鑰重新加密資料併發送給 *B*。
- 攻擊者傳送其公鑰作為A的公鑰，以便B將其視為來自A。
側通道攻擊 (SCA) − 此類攻擊並非針對任何特定型別的密碼系統或演算法。相反，它旨在利用密碼系統物理實現中的弱點。
定時攻擊 − 它們利用不同計算在處理器上花費不同時間這一事實。透過測量這些時間，可以瞭解處理器正在執行的特定計算。例如，如果加密花費的時間更長，則表示金鑰較長。
功耗分析攻擊 − 這些攻擊類似於定時攻擊，只是使用功耗量來獲取有關底層計算性質的資訊。
故障分析攻擊 − 在這些攻擊中，密碼系統中會引入錯誤，攻擊者會研究由此產生的輸出以獲取有用的資訊。

攻擊的實用性

此處描述的針對密碼系統的攻擊在很大程度上是學術性的，因為其中大部分來自學術界。事實上，許多學術攻擊都涉及對環境以及攻擊者能力相當不現實的假設。例如，在選擇密文攻擊中，攻擊者需要數量不切實際的故意選擇的明文-密文對。它可能根本不實用。

儘管如此，任何攻擊的存在都應該引起關注，特別是如果攻擊技術有可能改進。

傳統密碼

在第二章中，我們討論了現代密碼學的 fundamentals。我們將密碼學等同於一個工具箱，其中各種密碼技術被視為基本工具。這些工具之一是對稱金鑰加密，其中用於加密和解密的金鑰相同。

本章將進一步討論這項技術及其在開發各種密碼系統中的應用。

早期的密碼系統

在繼續之前，您需要了解一些關於歷史密碼系統的事實：

所有這些系統都基於對稱金鑰加密方案。
這些系統提供的唯一安全服務是資訊的機密性。
與將資料視為二進位制數字的現代數字系統不同，早期系統以字母為基本元素。

這些早期的密碼系統也稱為密碼。一般來說，密碼只是一組用於執行加密和相應解密的步驟（演算法）。

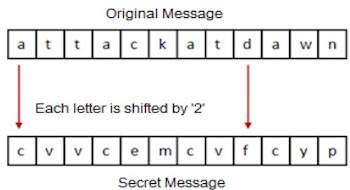
凱撒密碼

這是一種單字母替代密碼，其中明文的每個字母都被另一個字母替換以形成密文。它是最簡單的替換密碼方案。

該密碼系統通常被稱為移位密碼。其概念是用另一個“移位”了某個固定數字（0到25之間）的字母來替換每個字母。

對於這種方案，傳送方和接收方就字母的“秘密移位數字”達成一致。這個介於 0 和 25 之間的數字成為加密金鑰。

當使用“移位三”時，有時會使用“凱撒密碼”來描述移位密碼。

移位密碼的過程

為了加密明文字母，傳送方將滑動尺放在第一組明文字母下方，並將其向左滑動秘密移位的位數。
然後將明文字母加密為滑動尺下方的密文字母。對於商定的三個位置的移位，此過程的結果如下圖所示。在這種情況下，明文“tutorial”被加密為密文“WXWRULDO”。以下是移位 3 的密文字母表：

收到密文後，也瞭解秘密移位的接收方將滑動尺放在密文字母表下方，並將其向右滑動商定的移位數，在本例中為 3。
然後，他用滑動尺下方的明文字母替換密文字母。因此，密文“WXWRULDO”被解密為“tutorial”。要解密用移位 3 編碼的訊息，請使用“-3”的移位生成明文字母表，如下所示：

安全價值

凱撒密碼不是安全的密碼系統，因為只有 26 個可能的金鑰需要嘗試。攻擊者可以使用有限的可用計算資源進行窮舉金鑰搜尋。

簡單替換密碼

它是對凱撒密碼的改進。此方案不是將字母移位某個數字，而是使用字母的某種排列。

例如，A.B…..Y.Z 和 Z.Y……B.A 是字母表中所有字母的兩種明顯的排列。排列只不過是一組亂序的字母。

字母表中有 26 個字母，可能的排列是 26！（26 的階乘），等於 4x10²⁶。傳送方和接收方可以選擇這些可能的排列中的任何一個作為密文字母表。此排列是方案的秘密金鑰。

簡單替換密碼的過程

按自然順序編寫字母 A、B、C……Z。
傳送方和接收方確定字母表的隨機選擇的排列。
在自然順序字母下方，寫出所選字母排列。為了加密，傳送方透過替換表格中正下方對應的排列字母來替換每個明文字母。此過程如下圖所示。在這個例子中，選擇的排列是 K、D、G……O。明文“point”被加密為“MJBXZ”。

這是一個亂序的密文字母表，其中密文字母的順序是一個金鑰。

收到密文後，也瞭解隨機選擇的排列的接收方將底行中的每個密文字母替換為頂行中對應的明文字母。密文“MJBXZ”被解密為“point”。

安全價值

簡單替換密碼比凱撒密碼有了相當大的改進。可能的金鑰數量很大（26！），即使是現代計算系統也還不夠強大，無法輕鬆發起暴力攻擊來破解該系統。但是，簡單替換密碼設計簡單，容易出現設計缺陷，例如選擇明顯的排列，這個密碼系統很容易被破解。

單字母和多字母密碼

單字母密碼是一種替換密碼，其中對於給定的金鑰，每個明文字母的密碼字母在整個加密過程中都是固定的。例如，如果“A”被加密為“D”，則在該明文中出現任意次數，“A”將始終被加密為“D”。

本章前面討論的所有替換密碼都是單字母的；這些密碼極易受到密碼分析的影響。

多字母密碼是一種替換密碼，其中明文字母的密碼字母在加密過程中不同位置可能不同。接下來的兩個例子，Playfair 密碼和 Vigenere 密碼是多字母密碼。

Playfair 密碼

在此方案中，加密的是字母對，而不是像簡單替換密碼那樣單個字母。

在 Playfair 密碼中，最初建立一個金鑰表。金鑰表是一個 5×5 的字母網格，用作加密明文的金鑰。所有 25 個字母必須是唯一的，並且字母表中的一個字母（通常是 J）被省略，因為我們只需要 25 個字母而不是 26 個。如果明文包含 J，則將其替換為 I。

傳送方和接收方確定一個特定的金鑰，例如“tutorials”。在金鑰表中，表中的第一個字元（從左到右）是該短語，不包括重複的字母。表中的其餘部分將按自然順序填充字母表中剩餘的字母。金鑰表如下所示：

Playfair 密碼的過程

首先，將明文訊息分成兩字母的組（雙字母）。如果字母數量為奇數，則在最後一個字母后新增 Z。假設我們要加密訊息“hide money”。它將被寫成：

HI DE MO NE YZ
加密規則如下：
- 如果兩個字母都在同一列中，則取每個字母下方的字母（如果在底部則返回頂部）

T	U	O	R	I	“H”和“I”在同一列中，因此取它們下方的字母進行替換。HI → QC
A	L	S	B	C
D	E	F	G	H
K	M	N	P	Q
V	W	X	Y	Z

如果兩個字母都在同一行中，則取每個字母右邊的字母（如果在最右邊則返回左邊）

T	U	O	R	I	“D”和“E”在同一行中，因此取它們右邊的字母進行替換。DE → EF
A	L	S	B	C
D	E	F	G	H
K	M	N	P	Q
V	W	X	Y	Z

如果前面兩個規則都不成立，則用這兩個字母形成一個矩形，並取矩形水平對角上的字母。

使用這些規則，“hide money”使用“tutorials”金鑰加密的結果將是：

QC EF NU MF ZV

Playfair 密碼的解密與反向執行相同的過程一樣簡單。接收方擁有相同的金鑰，可以建立相同的金鑰表，然後解密使用該金鑰製作的任何訊息。

安全價值

它也是一種替換密碼，與簡單替換密碼相比更難破解。與替換密碼一樣，Playfair 密碼也可能受到密碼分析的影響，但是它針對的是 625 個可能的字母對（25x25 個字母），而不是 26 個不同的可能的字母。

Playfair 密碼主要用於保護重要但不關鍵的秘密，因為它使用快捷，不需要特殊裝置。

Vigenere 密碼

這種密碼方案使用文字字串（例如，一個單詞）作為金鑰，然後將其用於對明文進行多次移位。

例如，假設金鑰是“point”。金鑰的每個字母都轉換為其相應的數值：在這種情況下，

p → 16，o → 15，i → 9，n → 14，t → 20。

因此，金鑰是：16 15 9 14 20。

維吉尼亞密碼的過程

傳送方和接收方確定一個金鑰。假設金鑰是“point”。此金鑰的數字表示是“16 15 9 14 20”。
傳送方想要加密訊息，例如“attack from south east”。他將明文和數字金鑰排列如下：

他現在將每個明文字母按其下方的數字移動以建立密文，如下所示：

這裡，每個明文字元都移動了不同的數量——並且該數量由金鑰決定。金鑰必須小於或等於訊息的大小。
為了解密，接收方使用相同的金鑰並以相反的順序移動收到的密文以獲得明文。

安全價值

維吉尼亞密碼的設計是對標準凱撒密碼的改進，以降低對密文的密碼分析的有效性，並使密碼系統更強大。它比普通的凱撒密碼安全得多。

歷史上，它經常用於保護敏感的政治和軍事資訊。由於它對密碼分析造成的困難，它被稱為不可破的密碼。

維吉尼亞密碼的變體

維吉尼亞密碼有兩種特殊情況：

關鍵字長度與明文訊息相同。這種情況稱為維爾南密碼。它比典型的維吉尼亞密碼更安全。
維吉尼亞密碼成為具有完美保密性的密碼系統，稱為一次性密碼本。

一次性密碼本

情況如下：

關鍵字的長度與明文的長度相同。
關鍵字是由字母組成的隨機生成的字串。
關鍵字僅使用一次。

安全價值

讓我們比較移位密碼和一次性密碼本。

移位密碼——易於破解

在移位密碼的情況下，整個訊息可能具有 1 到 25 之間的移位。這是一個非常小的範圍，很容易進行暴力破解。但是，由於每個字元現在都有其自身的 1 到 26 之間的個體移位，因此對於訊息而言，可能的金鑰呈指數級增長。

一次性密碼本——不可能破解

假設我們用一次性密碼本加密名稱“point”。這是一個 5 個字母的文字。要透過暴力破解來破解密文，你需要嘗試所有可能的金鑰，並對 (26 x 26 x 26 x 26 x 26) = 26⁵ = 11881376 次進行計算。這是對於包含 5 個字母的訊息而言。因此，對於更長的訊息，計算量會隨著每個額外字母的增加而呈指數級增長。這使得透過暴力破解計算上不可能破解密文。

置換密碼

這是另一種型別的密碼，其中明文中字母的順序被重新排列以建立密文。實際的明文字母不會被替換。

一個例子是“簡單的列置換”密碼，其中明文以一定的字母寬度水平書寫。然後，密文按如下所示垂直讀取。

例如，明文是“golden statue is in eleventh cave”，選擇的秘密隨機金鑰是“five”。我們將此文字水平排列在列數等於金鑰值的表中。生成的文字如下所示。

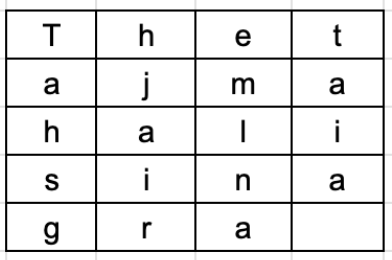
密文透過從第一列到最後一列垂直向下讀取列獲得。密文是“gnuneaoseenvltiltedasehetivc”。

為了解密，接收方準備類似的表格。列數等於金鑰數字。行數透過將密文字母總數除以金鑰值並將商四捨五入到下一個整數值來獲得。

然後，接收方垂直向下並從左到右列寫入收到的密文。為了獲得文字，他從左到右水平讀取，從上到下讀取行。

現代對稱金鑰加密

數字資料用二進位制數字（位）字串表示，不像字母那樣。現代密碼系統需要處理這些二進位制字串，將其轉換為另一個二進位制字串。根據如何處理這些二進位制字串，對稱加密方案可以分為：

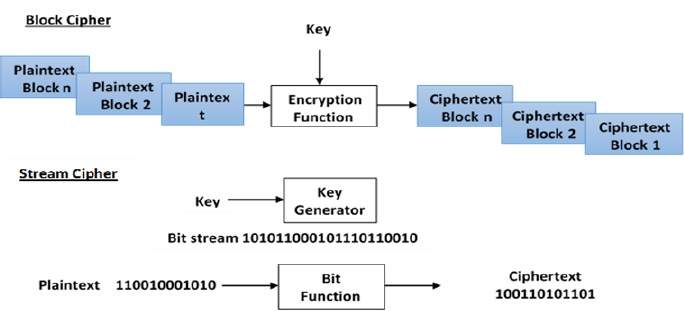
分組密碼

在這個方案中，明文二進位制文字一次處理成塊（組）位；即選擇明文位塊，對該塊執行一系列操作以生成密文位塊。塊中的位數是固定的。例如，DES 和 AES 方案的塊大小分別為 64 和 128。

流密碼

在這個方案中，明文一次處理一位，即取一位明文，對其執行一系列操作以生成一位密文。從技術上講，流密碼是塊大小為一位的塊密碼。

分組密碼

分組密碼的基本方案如下所示：

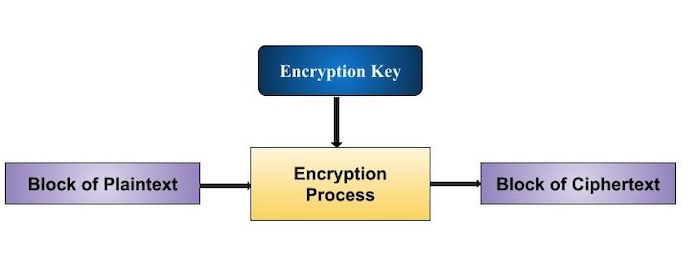
分組密碼接收明文位塊並生成密文位塊，通常大小相同。塊的大小在給定的方案中是固定的。塊大小的選擇不會直接影響加密方案的強度。密碼的強度取決於金鑰長度。

分組大小

雖然任何大小的塊都是可以接受的，但在選擇塊大小時應牢記以下幾個方面。

避免非常小的塊大小——假設塊大小為 m 位。則可能的明文位組合為 2^m。如果攻擊者發現了對應於某些先前傳送的密文塊的明文塊，則攻擊者可以透過建立已傳送使用該加密金鑰的明文/密文對的字典來發起一種“字典攻擊”。更大的塊大小使攻擊更加困難，因為字典需要更大。
不要有非常大的塊大小——對於非常大的塊大小，密碼的操作效率會降低。此類明文需要在加密之前進行填充。
8 位的倍數——首選的塊大小是 8 的倍數，因為它易於實現，因為大多數計算機處理器處理的資料都是 8 位的倍數。

分組密碼中的填充

分組密碼處理固定大小的塊（例如 64 位）。明文的長度大多不是塊大小的倍數。例如，150 位明文提供兩個 64 位塊，第三個塊剩餘 22 位。最後一個位塊需要用冗餘資訊填充，以便最後一個塊的長度等於方案的塊大小。在我們的例子中，剩餘的 22 位需要新增額外的 42 個冗餘位以提供一個完整的塊。向最後一個塊新增位的過程稱為填充。

過多的填充會使系統效率降低。此外，如果始終使用相同的位進行填充，則填充有時可能會使系統不安全。

分組密碼方案

有大量正在使用的分組密碼方案。其中許多都是公開已知的。下面列出了最流行和最突出的分組密碼。

數字加密標準 (DES)——20 世紀 90 年代流行的分組密碼。現在它被認為是一個“已破譯的”分組密碼，這主要是由於其金鑰大小較小。
三重 DES——它是一個基於重複 DES 應用的變體方案。它仍然是一個受人尊敬的分組密碼，但與現在可用的新型更快分組密碼相比效率較低。
高階加密標準 (AES)——它是一個相對較新的分組密碼，基於在 AES 設計競賽中獲勝的加密演算法Rijndael。
IDEA——它是一個足夠強大的分組密碼，塊大小為 64，金鑰大小為 128 位。許多應用程式使用 IDEA 加密，包括早期版本的 Pretty Good Privacy (PGP) 協議。由於專利問題，IDEA 方案的使用受到限制。
Twofish——這種分組密碼方案使用 128 位的塊大小和可變長度的金鑰。它是 AES 決賽選手之一。它基於早期塊大小為 64 位的分組密碼 Blowfish。
Serpent——一種塊大小為 128 位，金鑰長度為 128、192 或 256 位的分組密碼，也是 AES 競賽的決賽選手之一。它速度較慢，但設計比其他分組密碼更安全。

在接下來的部分中，我們將首先討論分組密碼模型，然後討論 DES 和 AES，這是兩個最具影響力的現代分組密碼。

Feistel 分組密碼

Feistel 密碼不是一種特定的分組密碼方案。它是一個設計模型，許多不同的分組密碼都是由此衍生出來的。DES 只是 Feistel 密碼的一個例子。基於 Feistel 密碼結構的密碼系統對加密和解密使用相同的演算法。

加密過程

加密過程使用 Feistel 結構，該結構由對明文的多次處理組成，每輪處理由“替換”步驟和置換步驟組成。

Feistel 結構如下圖所示：

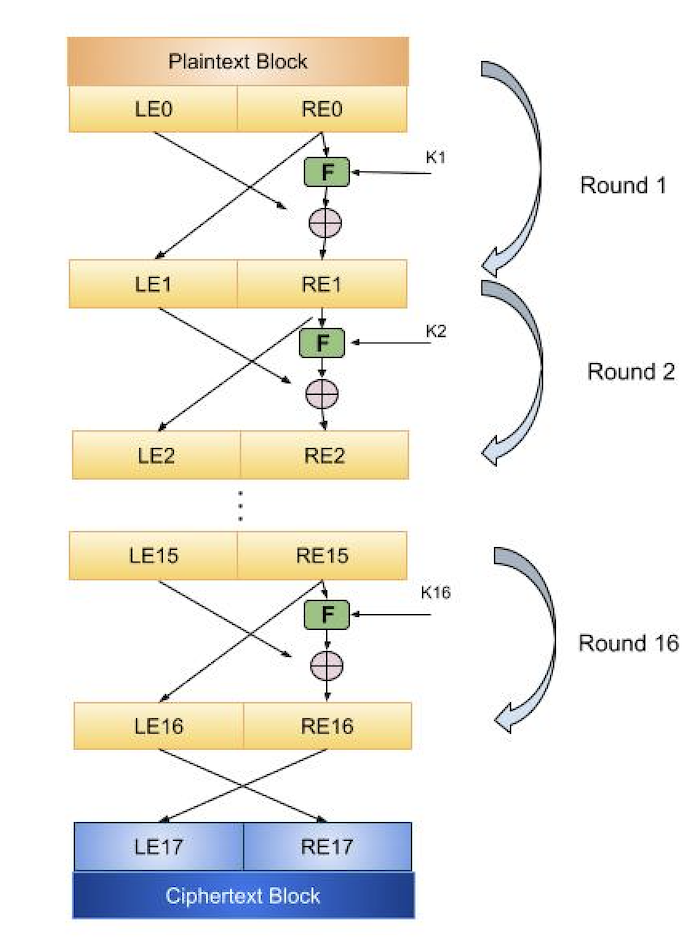
輸入到每一輪的塊被分成兩半，可以表示為 L（左半部分）和 R（右半部分）。
在每一輪中，塊的右半部分 R 保持不變。但是左半部分 L 會經歷一個取決於 R 和加密金鑰的操作。首先，我們應用一個加密函式“f”，它有兩個輸入——金鑰 K 和 R。該函式產生輸出 f(R,K)。然後，我們將數學函式的輸出與 L 進行異或。
在 Feistel 密碼的實際實現中，例如 DES，不是在每一輪中都使用整個加密金鑰，而是從加密金鑰中匯出一個依賴於輪次的金鑰（子金鑰）。這意味著每一輪使用不同的金鑰，儘管所有這些子金鑰都與原始金鑰相關。
每一輪結束時的置換步驟會交換修改後的 L 和未修改的 R。因此，下一輪的 L 將是當前輪的 R。下一輪的 R 將是當前輪的輸出 L。
上述替換和置換步驟構成一個“輪次”。輪數由演算法設計指定。
完成最後一輪後，兩個子塊“R”和“L”按此順序連線起來形成密文塊。

設計 Feistel 密碼的難點在於選擇輪函式“f”。為了使方案不可破，該函式需要具備一些重要的特性，這些特性超出了我們的討論範圍。

解密過程

Feistel 密碼的解密過程幾乎相同。只是不是以明文塊開始，而是將密文塊輸入 Feistel 結構的起始位置，然後接下來的過程與給定圖示中描述的完全相同。

之所以說是幾乎相同而不是完全相同，是因為在解密過程中，唯一的區別在於加密中使用的子金鑰以相反的順序使用。

Feistel 密碼最後一步中“L”和“R”的最終交換至關重要。如果不交換它們，則生成的密文將無法使用相同的演算法解密。

輪數

Feistel 密碼中使用的輪數取決於系統所需的安全性。輪數越多，系統越安全。但與此同時，輪數越多意味著加密和解密過程效率越低，速度越慢。因此，系統中的輪數取決於效率與安全性的權衡。

資料加密標準

資料加密標準 (DES) 是美國國家標準與技術研究院 (NIST) 釋出的對稱金鑰分組密碼。

DES 是 Feistel 密碼的一種實現。它使用 16 輪 Feistel 結構。分組大小為 64 位。雖然金鑰長度為 64 位，但 DES 的有效金鑰長度為 56 位，因為 64 位金鑰中的 8 位沒有被加密演算法使用（僅用作校驗位）。DES 的總體結構如下圖所示：

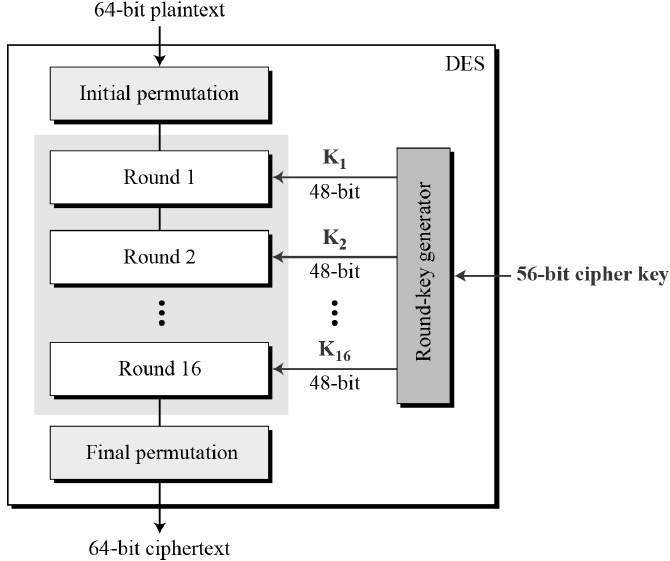
由於 DES 基於 Feistel 密碼，因此只需要指定以下內容即可：

輪函式
金鑰排程
任何其他處理：初始置換和最終置換

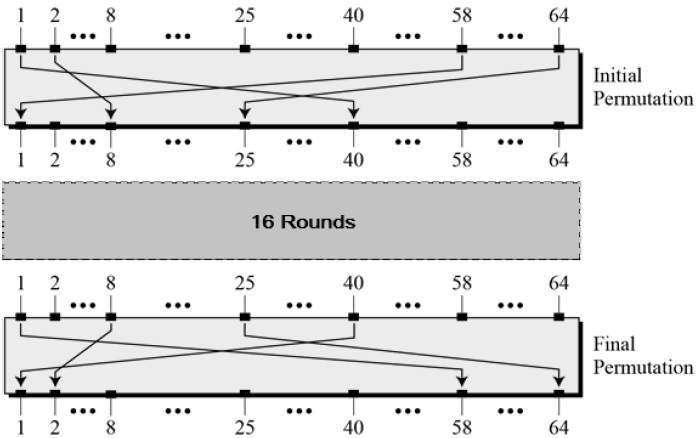
初始置換和最終置換

初始置換和最終置換是彼此互逆的簡單置換盒 (P 盒)。它們在 DES 中沒有密碼學意義。初始置換和最終置換如下所示：

輪函式

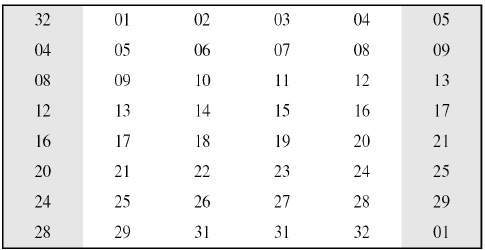
該密碼的核心是 DES 函式 f。DES 函式將 48 位金鑰應用於最右邊的 32 位，以產生 32 位輸出。

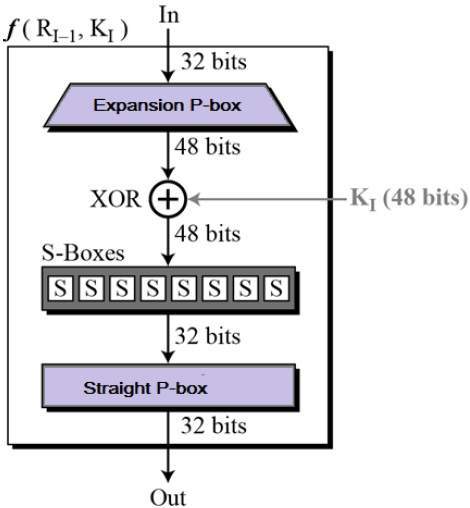
擴充套件置換盒：由於右側輸入為 32 位，而輪金鑰為 48 位，因此我們首先需要將右側輸入擴充套件到 48 位。置換邏輯如下圖所示：

DES 規範中通常將圖示的置換邏輯描述為表格，如下所示：

異或 (白化)：擴充套件置換後，DES 對擴充套件的右側部分和輪金鑰進行異或運算。輪金鑰僅在此操作中使用。
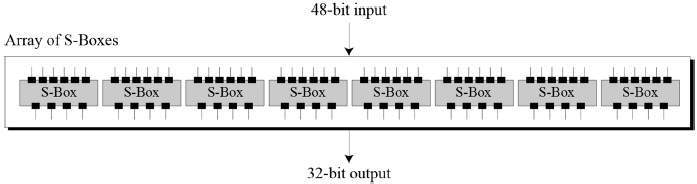
替代盒：S 盒執行真正的混合 (混淆)。DES 使用 8 個 S 盒，每個 S 盒都有 6 位輸入和 4 位輸出。請參考下圖：

S 盒規則如下所示：

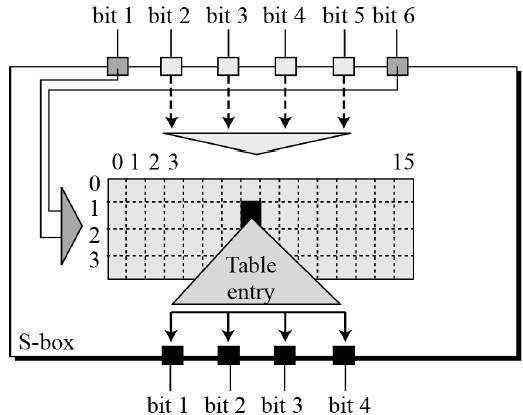
共有八個 S 盒表格。然後將所有八個 S 盒的輸出組合成 32 位部分。
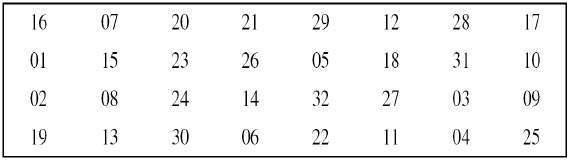
簡單置換：然後，S 盒的 32 位輸出將進行簡單置換，規則如下圖所示：

金鑰生成

輪金鑰生成器從 56 位密碼金鑰中建立十六個 48 位金鑰。金鑰生成過程如下圖所示：

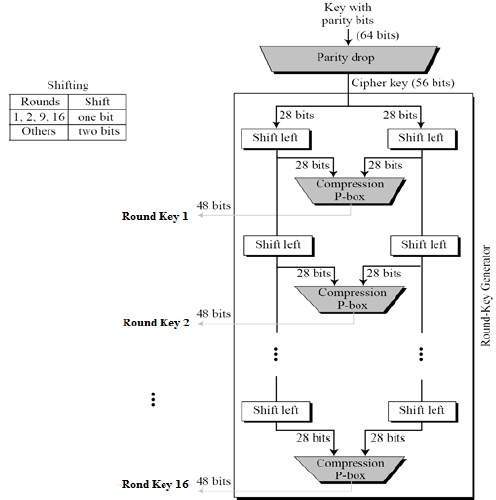
奇偶校驗丟棄、移位和壓縮 P 盒的邏輯在 DES 說明中給出。

DES 分析

DES 滿足分組密碼所需的兩個屬性。這兩個屬性使密碼非常強大。

雪崩效應：明文中的微小變化會導致密文中非常大的變化。
完整性：密文的每一位都依賴於許多位的明文。

在過去幾年中，密碼分析發現，當選擇的金鑰是弱金鑰時，DES 存在一些弱點。這些金鑰應避免使用。

DES已被證明是一個設計非常精良的分組密碼。除了窮舉金鑰搜尋之外，沒有針對 DES 的重大密碼分析攻擊。

三重 DES

1990 年之後，針對 DES 的窮舉金鑰搜尋速度開始引起 DES 使用者的不適。然而，使用者並不想更換 DES，因為更換已被廣泛採用並嵌入大型安全架構中的加密演算法需要花費大量時間和金錢。

務實的做法不是完全放棄 DES，而是改變 DES 的使用方式。這導致了三重 DES（有時稱為 3DES）的改進方案。

順便說一下，三重 DES 有兩種變體，分別稱為 3 金鑰三重 DES (3TDES) 和 2 金鑰三重 DES (2TDES)。

3 金鑰三重 DES

在使用 3TDES 之前，使用者首先要生成和分發 3TDES 金鑰 K，它由三個不同的 DES 金鑰 K₁、K₂ 和 K₃ 組成。這意味著實際的 3TDES 金鑰長度為 3×56 = 168 位。加密方案如下圖所示：

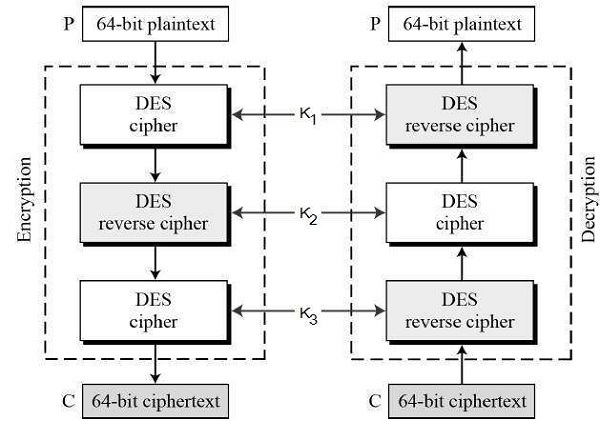
加密解密過程如下：

使用金鑰 K₁ 使用單 DES 加密明文塊。
現在使用金鑰 K₂ 使用單 DES 解密步驟 1 的輸出。
最後，使用金鑰 K₃ 使用單 DES 加密步驟 2 的輸出。
步驟 3 的輸出是密文。
密文的解密是一個反向過程。使用者首先使用 K₃ 解密，然後使用 K₂ 加密，最後使用 K₁ 解密。

由於三重 DES 被設計為加密-解密-加密過程，因此可以透過將 K₁、K₂ 和 K₃ 設定為相同的值來使用 3TDES（硬體）實現單 DES。這提供了與 DES 的向後相容性。

三重 DES 的第二個變體 (2TDES) 與 3TDES 相同，只是 K₃ 被 K₁ 替換。換句話說，使用者使用金鑰 K₁ 加密明文塊，然後使用金鑰 K₂ 解密，最後再次使用 K₁ 加密。因此，2TDES 的金鑰長度為 112 位。

三重 DES 系統比單 DES 安全得多，但它們顯然比使用單 DES 加密的過程慢得多。

高階加密標準 (AES)

如今可能遇到的更流行和廣泛採用的對稱加密演算法是高階加密標準 (AES)。它至少比三重 DES 快六倍。

由於 DES 的金鑰大小太小，因此需要替換它。隨著計算能力的提高，它被認為容易受到窮舉金鑰搜尋攻擊。三重 DES 的設計是為了克服這個缺點，但它被發現速度很慢。

AES 的特點如下：

對稱金鑰對稱分組密碼
128 位資料，128/192/256 位金鑰
比三重 DES 更強大、更快
提供完整的規範和設計細節
可在 C 和 Java 中實現的軟體

AES 的操作

AES 是一種迭代密碼，而不是 Feistel 密碼。它基於“替代-置換網路”。它包括一系列連結操作，其中一些操作涉及用特定輸出替換輸入（替代），而另一些操作則涉及重新排列位（置換）。

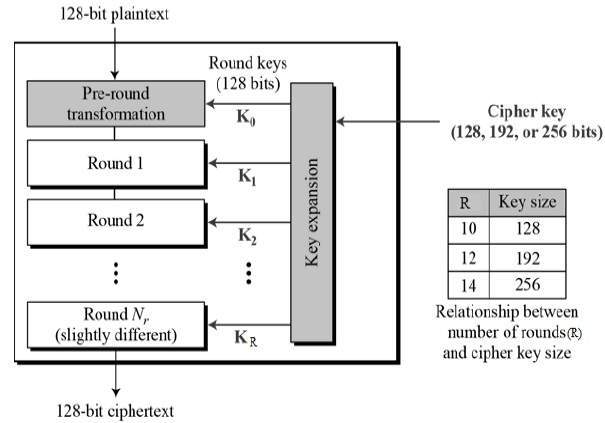
有趣的是，AES 執行的所有計算都是針對位元組而不是位進行的。因此，AES 將明文塊的 128 位視為 16 個位元組。這 16 個位元組被排列成四列四行，以矩陣形式進行處理：

與 DES 不同，AES 中的輪數是可變的，並且取決於金鑰的長度。對於 128 位金鑰，AES 使用 10 輪；對於 192 位金鑰，使用 12 輪；對於 256 位金鑰，使用 14 輪。每一輪都使用不同的 128 位輪金鑰，該金鑰是從原始 AES 金鑰計算出來的。

AES 結構示意圖如下所示：

加密過程

這裡，我們只介紹 AES 加密的典型輪次。每一輪都包含四個子過程。第一輪過程如下圖所示：

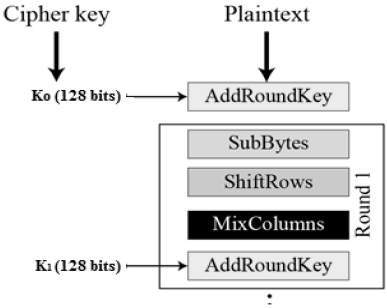
位元組替代 (SubBytes)

透過查詢設計中給出的固定表 (S 盒) 來替代 16 個輸入位元組。結果是一個四行四列的矩陣。

行移位 (ShiftRows)

矩陣的每一行都向左移動。任何“掉落”的條目都重新插入到行的右側。移位如下進行：

第一行不移位。
第二行向左移動一個（位元組）位置。
第三行向左移動兩個位置。
第四行向左移動三個位置。
結果是一個新的矩陣，它包含相同的 16 個位元組，但彼此之間發生了移位。

列混淆 (MixColumns)

現在使用特殊的數學函式變換四個位元組的每一列。此函式以一列的四個位元組作為輸入，並輸出四個全新的位元組，這些位元組替換原始列。結果是另一個包含 16 個新位元組的新矩陣。需要注意的是，在最後一輪中不執行此步驟。

輪金鑰加 (AddRoundKey)

矩陣的 16 個位元組現在被視為 128 位，並與輪金鑰的 128 位進行異或運算。如果這是最後一輪，則輸出是密文。否則，將結果 128 位解釋為 16 個位元組，然後我們開始另一輪類似的輪次。

解密過程

AES 密文的解密過程與加密過程類似，但順序相反。每一輪都包含四個以相反順序進行的子過程：

輪金鑰加
列混淆
行移位
位元組替代

由於每一輪中的子過程都是反向的，因此與 Feistel 密碼不同，加密和解密演算法需要單獨實現，儘管它們非常密切相關。

AES 分析

在當今的密碼學中，AES 被廣泛採用並在硬體和軟體中都得到支援。迄今為止，尚未發現針對 AES 的任何實際密碼分析攻擊。此外，AES 具有內建的金鑰長度靈活性，這使得它能夠在一定程度上“面向未來”，以應對窮舉金鑰搜尋能力的進步。

但是，與 DES 一樣，只有正確實現 AES 並採用良好的金鑰管理才能確保 AES 的安全性。

分組密碼的工作模式

本章將討論分組密碼的不同操作模式。這些是通用分組密碼的程式規則。有趣的是，不同的模式會導致實現不同的屬性，從而增強底層分組密碼的安全性。

分組密碼處理固定大小的資料塊。通常，訊息的大小大於塊大小。因此，長訊息被分成一系列連續的訊息塊，密碼一次對這些塊進行操作。

電子密碼本 (ECB) 模式

此模式是處理一系列連續列出的訊息塊的最直接方法。

操作

使用者取明文的第一塊，用金鑰加密它，產生密文的第一塊。
然後，他取明文的第二塊，用相同的金鑰重複相同的過程，以此類推。

ECB模式是**確定性**的，也就是說，如果明文塊P1、P2……Pm用相同的金鑰加密兩次，輸出的密文塊將相同。

事實上，對於給定的金鑰，從技術上講，我們可以為所有可能的明文塊建立一個密文程式碼本。加密將只需要查詢所需的明文並選擇相應的密文。因此，該操作類似於在程式碼本中分配程式碼字，因此獲得了正式名稱——電子密碼本操作模式（ECB）。如下圖所示：

ECB模式分析

實際上，任何應用程式資料通常都包含可以猜測的部分資訊。例如，可以猜測工資範圍。如果明文訊息在可預測範圍內，則來自ECB的密文可以允許攻擊者透過反覆試驗來猜測明文。

例如，如果已知來自ECB模式的密文加密的是工資數字，則少量嘗試將允許攻擊者恢復該數字。一般來說，我們不希望使用確定性密碼，因此在大多數應用程式中不應使用ECB模式。

密碼分組連結 (CBC) 模式

CBC操作模式提供訊息依賴性來生成密文，並使系統非確定性。

操作

CBC模式的操作如下圖所示。步驟如下：

將n位初始化向量（IV）載入到頂部暫存器中。
將n位明文塊與頂部暫存器中的資料值進行異或運算。
使用底層分組密碼和金鑰K加密異或運算的結果。
將密文塊送入頂部暫存器，並繼續操作，直到處理所有明文塊。
對於解密，IV資料與解密的第一個密文塊進行異或運算。第一個密文塊也被送入暫存器，替換IV以解密下一個密文塊。

CBC模式分析

在CBC模式中，當前明文塊被新增到之前的密文塊，然後結果用金鑰加密。因此，解密是相反的過程，包括解密當前密文，然後將之前的密文塊新增到結果中。

CBC優於ECB的優點是更改IV會導致相同訊息的密文不同。缺點是，由於鏈式效應，傳輸中的錯誤會在解密期間傳播到幾個後續塊。

值得一提的是，CBC模式構成了眾所周知的資料來源認證機制的基礎。因此，對於那些需要對稱加密和資料來源認證的應用程式，它具有優勢。

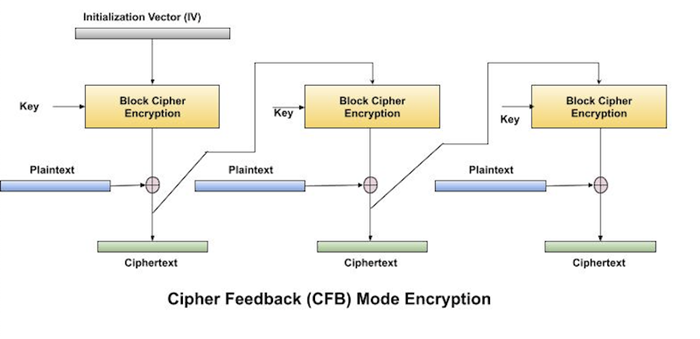
密碼反饋 (CFB) 模式

在此模式下，每個密文塊都被“反饋”到加密過程中，以便加密下一個明文塊。

操作

CFB模式的操作如下圖所示。例如，在本系統中，訊息塊的大小為“s”位，其中1 < s < n。CFB模式需要一個初始化向量（IV）作為初始隨機n位輸入塊。IV不需要保密。操作步驟如下：

將IV載入到頂部暫存器中。
使用底層分組密碼和金鑰K加密頂部暫存器中的資料值。
僅取加密過程輸出的“s”個最高有效位（左位），並將它們與“s”位明文訊息塊進行異或運算，以生成密文塊。
透過將已有的資料左移，將密文塊送入頂部暫存器，並繼續操作，直到處理所有明文塊。
本質上，之前的密文塊用金鑰加密，然後結果與當前明文塊進行異或運算。
解密也遵循類似的步驟。預先確定的IV最初在解密開始時載入。

CFB模式分析

CFB模式與ECB模式有很大不同，給定明文塊對應的密文不僅取決於該明文塊和金鑰，還取決於之前的密文塊。換句話說，密文塊取決於訊息。

CFB有一個非常奇怪的特性。在此模式下，使用者僅使用分組密碼的加密過程來解密密文。從不使用底層分組密碼的解密演算法。

顯然，CFB模式正在將分組密碼轉換為一種流密碼。加密演算法用作金鑰流生成器，以生成放置在底部暫存器中的金鑰流。然後，此金鑰流與明文進行異或運算，就像流密碼的情況一樣。

透過將分組密碼轉換為流密碼，CFB模式提供了一些流密碼的優點，同時保留了分組密碼的優點。

另一方面，由於塊的更改，傳輸錯誤會傳播。

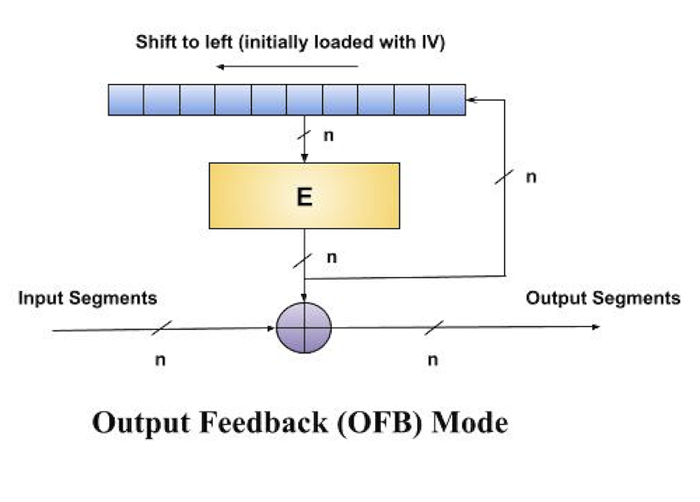
輸出反饋 (OFB) 模式

它涉及將來自底層分組密碼的連續輸出塊反饋給它。這些反饋塊提供了一系列位來饋送加密演算法，該演算法充當金鑰流生成器，就像在CFB模式中一樣。

生成的金鑰流與明文塊進行異或運算。OFB模式需要一個IV作為初始隨機n位輸入塊。IV不需要保密。

操作如下圖所示：

計數器 (CTR) 模式

它可以被認為是無反饋的CFB模式的基於計數器的版本。在此模式下，傳送方和接收方都需要訪問可靠的計數器，該計數器每次交換密文塊時都會計算一個新的共享值。此共享計數器不一定是秘密值，但挑戰在於雙方必須保持計數器的同步。

操作

CTR模式中的加密和解密如下圖所示。操作步驟如下：

載入頂部暫存器中的初始計數器值對於傳送方和接收方都是相同的。它在CFB（和CBC）模式中扮演與IV相同的作用。
使用金鑰加密計數器的內容，並將結果放置在底部暫存器中。
取第一個明文塊P1並將其與底部暫存器的內容進行異或運算。結果為C1。將C1傳送到接收方並更新計數器。計數器更新替換了CFB模式中的密文反饋。
繼續以這種方式進行，直到加密最後一個明文塊。
解密是相反的過程。密文塊與加密的計數器值的輸出進行異或運算。在每個密文塊解密後，計數器都會像加密一樣更新。

計數器模式分析

它沒有訊息依賴性，因此密文塊不依賴於之前的明文塊。

與CFB模式一樣，CTR模式不涉及分組密碼的解密過程。這是因為CTR模式實際上是使用分組密碼生成金鑰流，該金鑰流使用XOR函式加密。換句話說，CTR模式也將分組密碼轉換為流密碼。

CTR模式的一個嚴重缺點是它需要傳送方和接收方具有同步計數器。同步丟失會導致明文恢復不正確。

但是，CTR模式幾乎具有CFB模式的所有優點。此外，它根本不會傳播傳輸錯誤。

公鑰加密

公鑰密碼術

與對稱金鑰密碼術不同，我們沒有發現公鑰密碼術的歷史用途。這是一個相對較新的概念。

對稱密碼術非常適合政府、軍隊和大型金融公司等參與機密通訊的組織。

在過去幾十年中，隨著越來越多的不安全的計算機網路的普及，人們感到需要大規模使用密碼術。由於對稱金鑰在金鑰管理方面面臨挑戰，因此發現它不切實際。這導致了公鑰密碼系統的出現。

加密和解密過程如下圖所示：

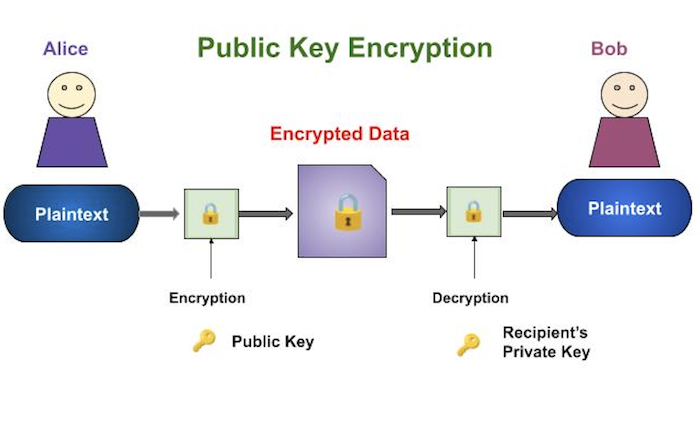
公鑰加密方案最重要的屬性是：

加密和解密使用不同的金鑰。這是使此方案不同於對稱加密方案的屬性。
每個接收者擁有一個唯一的解密金鑰，通常稱為其私鑰。
接收者需要釋出一個加密金鑰，稱為其公鑰。
此方案需要對公鑰的真實性進行一些保證，以避免被對手冒充為接收者。通常，這種型別的密碼系統涉及可信賴的第三方，該第三方證明特定的公鑰只屬於特定的人或實體。
加密演算法足夠複雜，可以阻止攻擊者從密文和加密（公鑰）中推斷出明文。
儘管私鑰和公鑰在數學上是相關的，但從公鑰計算私鑰是不可行的。事實上，任何公鑰密碼系統的智慧部分都在於設計兩個金鑰之間的關係。

公鑰加密方案有三種類型。我們在以下部分討論它們：

RSA密碼系統

該密碼系統是最初的系統之一。即使在今天，它仍然是最常用的密碼系統。該系統由三位學者**Ron Rivest、Adi Shamir**和**Len Adleman**發明，因此被稱為RSA密碼系統。

我們將看到RSA密碼系統的兩個方面，首先是金鑰對的生成，其次是加密解密演算法。

RSA金鑰對的生成

每個希望使用加密參與通訊的人或一方都需要生成一對金鑰，即公鑰和私鑰。金鑰生成的流程如下：

生成RSA模數(n)
- 選擇兩個大素數，p 和 q。
- 計算 n=p*q。為了獲得強大的不可破解加密，n 應該是一個很大的數，通常至少 512 位。
尋找匯出數 (e)
- 數字e必須大於 1 且小於 (p − 1)(q − 1)。
- e 和 (p − 1)(q − 1) 之間除了 1 以外，不能有其他公因子。換句話說，e 和 (p – 1)(q – 1) 互質。
形成公鑰
- 數字對 (n, e) 構成 RSA 公鑰，並公開。
- 有趣的是，雖然 n 是公鑰的一部分，但大型素數難以分解確保攻擊者無法在有限時間內找到用於獲得 n 的兩個素數 (p & q)。這是 RSA 的優勢。
生成私鑰
- 私鑰 d 由 p、q 和 e 計算得出。對於給定的 n 和 e，存在唯一的數字 d。
- 數字 d 是 e 模 (p - 1)(q – 1) 的逆元。這意味著 d 是小於 (p - 1)(q - 1) 的數字，當它乘以 e 時，模 (p - 1)(q - 1) 等於 1。
- 這種關係可以用以下數學公式表示：

ed = 1 mod (p − 1)(q − 1)

擴充套件歐幾里德演算法以 p、q 和 e 為輸入，並以 d 為輸出。

示例

下面給出了生成 RSA 金鑰對的一個示例。（為了便於理解，這裡選擇的素數 p & q 值較小。實際上，這些值非常大）。

設兩個素數為 p = 7 和 q = 13。因此，模數 n = pq = 7 x 13 = 91。
選擇 e = 5，這是一個有效的選擇，因為除了 1 之外，5 和 (p − 1)(q − 1) = 6 × 12 = 72 沒有公因子。
數字對 (n, e) = (91, 5) 構成公鑰，可以提供給任何我們希望向其傳送加密訊息的人。
將 p = 7、q = 13 和 e = 5 輸入擴充套件歐幾里德演算法。輸出將為 d = 29。
透過計算以下內容來檢查計算出的 d 是否正確：

de = 29 × 5 = 145 = 1 mod 72

因此，公鑰是 (91, 5)，私鑰是 (91, 29)。

加密和解密

金鑰對生成後，加密和解密過程相對簡單，計算量也很小。

有趣的是，RSA 不直接對位串進行操作，就像對稱金鑰加密一樣。它對模 n 的數字進行操作。因此，有必要將明文表示為一系列小於 n 的數字。

RSA 加密

假設傳送方希望向公鑰為 (n, e) 的某人傳送文字訊息。
然後，傳送方將明文表示為一系列小於 n 的數字。
要加密第一個明文 P（它是模 n 的一個數字）。加密過程是一個簡單的數學步驟：

C = P^e mod n

換句話說，密文 C 等於明文 P 自乘 e 次，然後模 n。這意味著 C 也是小於 n 的數字。
回到我們的金鑰生成示例，明文 P = 10，我們得到密文 C：

C = 10⁵ mod 91

RSA 解密

RSA 的解密過程也很簡單。假設公鑰對 (n, e) 的接收方收到了密文 C。
接收方將 C 乘方到其私鑰 d。模 n 的結果將是明文 P。

Plaintext = C^d mod n

再次回到我們的數值示例，密文 C = 82 將使用私鑰 29 解密為數字 10：

Plaintext = 82²⁹ mod 91 = 10

RSA 分析

RSA 的安全性取決於兩個獨立函式的強度。RSA 密碼系統是最流行的公鑰密碼系統，其強度基於對非常大的數字進行因式分解的實際難度。

加密函式：它被認為是一個將明文轉換為密文的一維函式，只有知道私鑰 d 才能將其反轉。
金鑰生成：從 RSA 公鑰確定私鑰的難度等同於對模數 n 進行因式分解。因此，除非攻擊者能夠對 n 進行因式分解，否則他無法使用 RSA 公鑰的知識來確定 RSA 私鑰。這也是一個單向函式，從 p & q 值到模數 n 很容易，但反過來則不可能。

如果這兩個函式中的任何一個都被證明不是單向函式，那麼 RSA 將被破解。事實上，如果開發出一種有效的因式分解技術，那麼 RSA 將不再安全。

如果 p 和 q 不是大素數和/或選擇的公鑰 e 是一個小數，則 RSA 加密的強度會大幅下降。

ElGamal 密碼系統

除了 RSA 之外，還提出了其他公鑰密碼系統。它們中的許多都基於離散對數問題的不同版本。

ElGamal 密碼系統（稱為橢圓曲線變體）基於離散對數問題。它的強度源於這樣的假設：對於給定的數字，在實際時間範圍內無法找到離散對數，而冪的逆運算可以有效地計算。

讓我們來看一下 ElGamal 的一個簡單版本，它使用模 p 的數字。在橢圓曲線變體的情況下，它基於完全不同的數字系統。

ElGamal 金鑰對的生成

ElGamal 密碼系統的每個使用者都透過以下方式生成金鑰對：

選擇一個大素數 p。通常選擇長度為 1024 到 2048 位的素數。
選擇一個生成元 g。
- 這個數字必須在 1 和 p − 1 之間，但不能是任何數字。
- 它是模 p 整數乘法群的生成元。這意味著對於與 p 互質的每個整數 m，存在一個整數 k 使得 g^k=a mod n。
  
  例如，3 是群 5 (Z₅ = {1, 2, 3, 4}) 的生成元。

N	3ⁿ	3ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

選擇私鑰。私鑰 x 是任何大於 1 且小於 p−1 的數字。
計算公鑰的一部分。值 y 由引數 p、g 和私鑰 x 計算如下：

y = g^x mod p

獲得公鑰。ElGamal 公鑰由三個引數 (p, g, y) 組成。

例如，假設 p = 17 且 g = 6（可以確認 6 是群 Z₁₇ 的生成元）。私鑰 x 可以是任何大於 1 且小於 71 的數字，因此我們選擇 x = 5。然後計算值 y 如下：

y = 6⁵ mod 17 = 7

因此私鑰是 62，公鑰是 (17, 6, 7)。

加密和解密

與 RSA 相比，ElGamal 金鑰對的生成相對簡單。但是加密和解密比 RSA 稍微複雜一些。

ElGamal 加密

假設傳送方希望向 ElGamal 公鑰為 (p, g, y) 的某人傳送明文，則：

傳送方將明文表示為一系列模 p 的數字。
要加密第一個明文 P（表示為模 p 的數字）。獲得密文 C 的加密過程如下：
- 隨機生成一個數字 k；
- 計算兩個值 C1 和 C2，其中：

C1 = g^k mod p
C2 = (P^*y^k) mod p

一起傳送由兩個單獨值 (C1, C2) 組成的密文 C。
參考上面給出的 ElGamal 金鑰生成示例，明文 P = 13 加密如下：
- 隨機生成一個數字，例如 k = 10
- 計算兩個值 C1 和 C2，其中：

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

傳送密文 C = (C1, C2) = (15, 9)。

ElGamal 解密

要使用私鑰 x 解密密文 (C1, C2)，需要執行以下兩個步驟：
- 計算 (C1)^x 模 p 的模逆元，即 (C1)^-x，通常稱為解密因子。
- 使用以下公式獲得明文：

C2 × (C1)^-x mod p = Plaintext

在我們的示例中，要使用私鑰 x = 5 解密密文 C = (C1, C2) = (15, 9)，解密因子為

15^-5 mod 17 = 9

提取明文 P = (9 × 9) mod 17 = 13。

ElGamal 分析

在 ElGamal 系統中，每個使用者都有一個私鑰 x，並具有公鑰的三個組成部分：素模數 p、生成元 g 和公鑰 Y = g^x mod p。ElGamal 的強度基於離散對數問題的難度。

安全金鑰大小通常 > 1024 位。如今甚至使用 2048 位長的金鑰。在處理速度方面，ElGamal 相當慢，它主要用於金鑰身份驗證協議。由於更高的處理效率，ElGamal 的橢圓曲線變體正變得越來越流行。

橢圓曲線密碼術 (ECC)

橢圓曲線密碼術 (ECC) 用於描述一套密碼工具和協議，其安全性基於離散對數問題的特殊版本。它不使用模 p 的數字。

ECC 基於與稱為橢圓曲線的數學物件相關的數字集。存在新增和計算這些數字倍數的規則，就像模 p 的數字一樣。

ECC 包括許多最初為模數設計的密碼方案的變體，例如 ElGamal 加密和數字簽名演算法。

人們認為，當應用於橢圓曲線上的點時，離散對數問題要困難得多。這促使人們從模 p 的數字切換到橢圓曲線上的點。如果我們使用基於橢圓曲線的變體，也可以獲得等效的安全級別，而金鑰長度更短。

較短的金鑰帶來兩個好處：

金鑰管理簡便
高效計算

這些優點使基於橢圓曲線的加密方案變體對於計算資源受限的應用非常有吸引力。

RSA 和 ElGamal 方案——比較

讓我們簡要比較一下 RSA 和 ElGamal 方案的各個方面。

RSA	ElGamal
加密效率更高。	解密效率更高。
解密效率較低。	解密效率更高。
對於特定的安全級別，RSA 需要較長的金鑰。	對於相同的安全級別，需要非常短的金鑰。
它被廣泛接受和使用。	它比較新，在市場上並不流行。

密碼學中的資料完整性

到目前為止，我們討論了使用對稱和公鑰方案來實現資訊機密性。本章開始討論旨在提供其他安全服務的不同密碼技術。

本章重點關注資料完整性和用於實現相同目標的密碼工具。

對資料完整性的威脅

交換敏感資訊時，接收方必須確信訊息完整地來自預期的傳送方，並且不會無意中或以其他方式被修改。存在兩種不同型別的資料完整性威脅，即被動和主動。

被動威脅

此類威脅是由於資料的意外更改而存在的。

這些資料錯誤可能是由於通訊通道中的噪聲引起的。此外，資料在磁碟上儲存時也可能損壞。
糾錯碼和簡單的校驗和（如迴圈冗餘校驗 (CRC)）用於檢測資料完整性丟失。在這些技術中，資料的摘要是透過數學計算計算出來的，並附加到資料中。

主動威脅

在這種型別的威脅中，攻擊者可以惡意操縱資料。

在最簡單的層面上，如果資料沒有摘要，則可以修改資料而不會被檢測到。系統可以使用附加 CRC 到資料的方法來檢測任何主動修改。
在更高層次的威脅中，攻擊者可能會修改資料並嘗試從現有摘要中為修改後的資料匯出新的摘要。如果使用簡單的機制（如 CRC）計算摘要，則這是可能的。
諸如雜湊函式之類的安全機制用於解決主動修改威脅。

密碼學雜湊函式

雜湊函式極其有用，幾乎出現在所有資訊安全應用中。

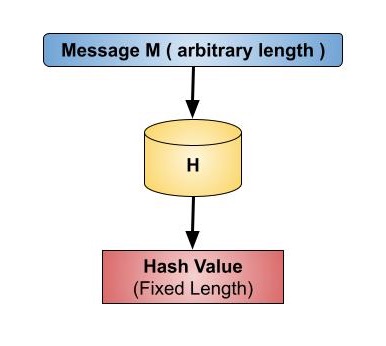
雜湊函式是一種數學函式，它將數值輸入值轉換為另一個壓縮的數值值。雜湊函式的輸入長度是任意的，但輸出長度始終是固定的。

雜湊函式返回的值稱為訊息摘要或簡稱為雜湊值。下圖說明了雜湊函式：

雜湊函式的特徵

雜湊函式的典型特徵如下：

固定長度的輸出（雜湊值）
- 雜湊函式將任意長度的資料轉換為固定長度的資料。這個過程通常被稱為對資料進行雜湊。
- 通常情況下，雜湊值遠小於輸入資料，因此雜湊函式有時也被稱為壓縮函式。
- 由於雜湊值是較大資料的較小表示，因此它也稱為摘要。
- 具有n位輸出的雜湊函式被稱為n位雜湊函式。流行的雜湊函式生成的雜湊值長度在160到512位之間。
運算效率
- 通常，對於任何輸入為x的雜湊函式h，計算h(x)是一個快速操作。
- 在計算上，雜湊函式比對稱加密快得多。

雜湊函式的特性

為了成為有效的密碼工具，雜湊函式需要具備以下特性：

抗原像性
- 此特性意味著反轉雜湊函式在計算上應該是困難的。
- 換句話說，如果雜湊函式h產生了一個雜湊值z，那麼找到任何雜湊到z的輸入值x都應該是一個困難的過程。
- 此特性可以防止攻擊者只擁有雜湊值並試圖找到輸入。
抗第二原像性
- 此特性意味著，給定一個輸入及其雜湊值，應該很難找到另一個具有相同雜湊值的輸入。
- 換句話說，如果輸入為x的雜湊函式h產生雜湊值h(x)，那麼應該很難找到任何其他輸入值y，使得h(y) = h(x)。
- 雜湊函式的此特性可以防止攻擊者擁有一個輸入值及其雜湊值，並想用不同的值替換原始輸入值。
抗碰撞性
- 此特性意味著應該很難找到兩個不同的輸入（長度任意），它們產生相同的雜湊值。此特性也稱為無碰撞雜湊函式。
- 換句話說，對於雜湊函式h，很難找到任何兩個不同的輸入x和y，使得h(x) = h(y)。
- 由於雜湊函式是具有固定雜湊長度的壓縮函式，因此雜湊函式不可能沒有碰撞。無碰撞特性只確認這些碰撞應該很難找到。
- 此特性使得攻擊者很難找到兩個具有相同雜湊值的輸入值。
- 此外，如果雜湊函式具有抗碰撞性，那麼它也具有抗第二原像性。

雜湊演算法的設計

雜湊的核心是一個數學函式，它對兩個固定大小的資料塊進行運算以建立雜湊碼。此雜湊函式構成雜湊演算法的一部分。

每個資料塊的大小根據演算法的不同而不同。通常資料塊的大小從128位到512位不等。下圖演示了雜湊函式：

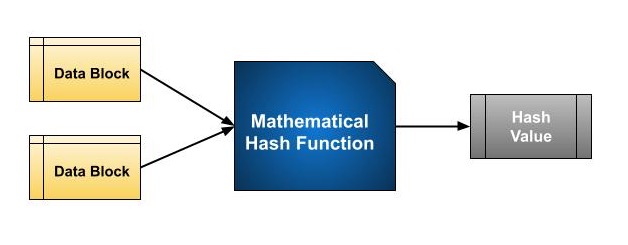
雜湊演算法涉及到像塊密碼一樣對上述雜湊函式進行多輪運算。每一輪都接收固定大小的輸入，通常是最近的訊息塊和上一輪輸出的組合。

此過程將重複進行足夠多的輪數，以對整個訊息進行雜湊運算。雜湊演算法的示意圖如下所示：

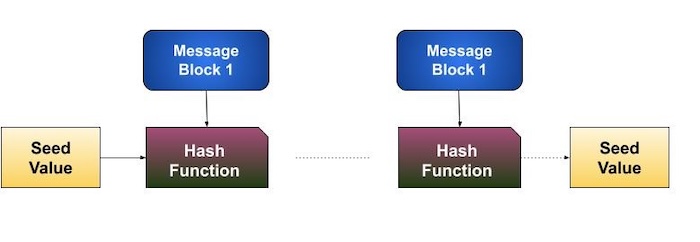
由於第一個訊息塊的雜湊值成為第二個雜湊運算的輸入，其輸出會改變第三個運算的結果，依此類推。這種效應被稱為雜湊的雪崩效應。

雪崩效應導致兩個即使只相差一位資料的郵件產生截然不同的雜湊值。

正確理解雜湊函式和演算法的區別。雜湊函式透過對兩個固定長度的二進位制資料塊進行運算來生成雜湊碼。

雜湊演算法是使用雜湊函式的過程，它指定了如何將訊息分解以及如何將先前訊息塊的結果連結在一起。

流行的雜湊函式

讓我們簡要了解一些流行的雜湊函式：

訊息摘要 (MD)

MD5在相當長的一段時間內是最流行和最廣泛使用的雜湊函式。

MD家族包括雜湊函式MD2、MD4、MD5和MD6。它被採納為網際網路標準RFC 1321。它是一個128位雜湊函式。
MD5摘要已廣泛用於軟體領域，以確保傳輸檔案的完整性。例如，檔案伺服器通常會為檔案提供預先計算的MD5校驗和，以便使用者可以將其與下載檔案的校驗和進行比較。
2004年，在MD5中發現了碰撞。據報道，使用計算機叢集只需一個小時就能成功進行分析攻擊。這種碰撞攻擊導致MD5遭到破壞，因此不再推薦使用。

安全雜湊演算法 (SHA)

SHA家族包括四種SHA演算法：SHA-0、SHA-1、SHA-2和SHA-3。雖然來自同一個家族，但在結構上有所不同。

原始版本SHA-0是一個160位的雜湊函式，於1993年由美國國家標準與技術研究院(NIST)釋出。它有一些弱點，並沒有流行起來。後來在1995年，設計了SHA-1來糾正SHA-0的所謂弱點。
SHA-1是現有的SHA雜湊函式中最廣泛使用的。它被用於包括安全套接字層(SSL)安全在內的幾個廣泛使用的應用程式和協議中。
2005年，人們找到了一種方法，可以在實際時間範圍內發現SHA-1的碰撞，這使得SHA-1的長期可用性令人懷疑。
SHA-2家族根據雜湊值的位數，還有四種SHA變體，分別是SHA-224、SHA-256、SHA-384和SHA-512。目前還沒有關於SHA-2雜湊函式的成功攻擊報告。
雖然SHA-2是一個強大的雜湊函式。雖然差異很大，但其基本設計仍然遵循SHA-1的設計。因此，NIST呼籲新的競爭性雜湊函式設計。
2012年10月，NIST選擇Keccak演算法作為新的SHA-3標準。Keccak具有許多優點，例如高效的效能和良好的抗攻擊能力。

RIPEMD

RIPEMD是RACE完整性基元評估訊息摘要的縮寫。這組雜湊函式是由開放研究社群設計的，通常被稱為歐洲雜湊函式家族。

該集合包括RIPEMD、RIPEMD-128和RIPEMD-160。該演算法還存在256位和320位版本。
原始RIPEMD（128位）基於MD4中使用的設計原則，並被發現提供安全性存疑。RIPEMD 128位版本作為快速修復替代方案出現，以克服原始RIPEMD的漏洞。
RIPEMD-160是改進版本，也是該家族中使用最廣泛的版本。256位和320位版本降低了意外碰撞的機率，但與RIPEMD-128和RIPEMD-160相比，其安全性並沒有更高。

Whirlpool

這是一個512位的雜湊函式。

它源自高階加密標準(AES)的修改版本。其中一位設計者是Vincent Rijmen，他是AES的共同建立者。
Whirlpool已經發布了三個版本：WHIRLPOOL-0、WHIRLPOOL-T和WHIRLPOOL。

雜湊函式的應用

基於雜湊函式的密碼特性，它有兩個直接的應用。

密碼儲存

雜湊函式提供密碼儲存保護。

大多數登入過程不是以明文儲存密碼，而是在檔案中儲存密碼的雜湊值。
密碼檔案由一系列成對的值組成，形式為(使用者ID, h(P))。
登入過程如下圖所示：

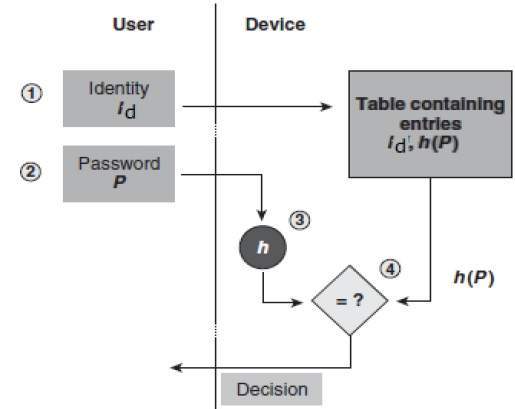
即使入侵者訪問了密碼檔案，也只能看到密碼的雜湊值。他既不能使用雜湊值登入，也不能從雜湊值推匯出密碼，因為雜湊函式具有抗原像性。

資料完整性檢查

資料完整性檢查是雜湊函式最常見的應用。它用於生成資料檔案的校驗和。此應用向用戶保證資料的正確性。

該過程如下圖所示：

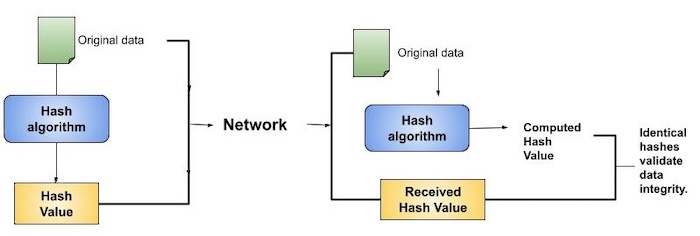
完整性檢查幫助使用者檢測對原始檔案所做的任何更改。但是，它不保證檔案的原始性。攻擊者可以更改整個檔案並計算一個全新的雜湊值併發送給接收者，而不是修改檔案資料。此完整性檢查應用程式僅在使用者確信檔案的原始性時才有效。

訊息認證

在上一章中，我們討論了資料完整性威脅以及使用雜湊技術來檢測資料是否發生任何修改攻擊。

資料存在的另一種威脅是缺乏訊息認證。在這種威脅中，使用者不確定訊息的傳送者。可以使用使用金鑰進行加密的密碼技術來提供訊息認證。

訊息認證碼 (MAC)

MAC演算法是一種對稱金鑰密碼技術，用於提供訊息認證。為了建立MAC過程，傳送方和接收方共享一個對稱金鑰K。

本質上，MAC是在底層訊息上生成的加密校驗和，它與訊息一起傳送以確保訊息認證。

使用MAC進行認證的過程如下圖所示：

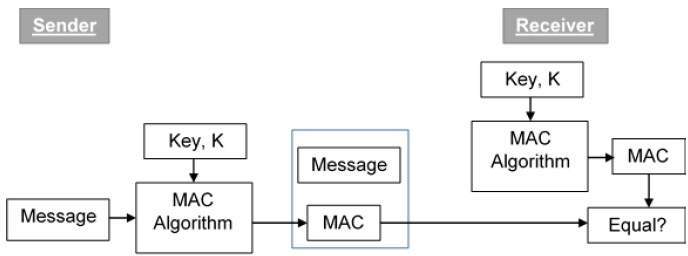
現在讓我們嘗試詳細瞭解整個過程：

傳送方使用一些公開的MAC演算法，輸入訊息和金鑰K，併產生一個MAC值。
與雜湊類似，MAC函式也壓縮任意長的輸入到固定長度的輸出。雜湊和MAC的主要區別在於MAC在壓縮過程中使用金鑰。
傳送方將訊息及其MAC一起轉發。在這裡，我們假設訊息以明文傳送，因為我們關注的是提供訊息來源認證，而不是機密性。如果需要機密性，則需要對訊息進行加密。
收到訊息和MAC後，接收方將接收到的訊息和共享金鑰K輸入MAC演算法並重新計算MAC值。
接收方現在檢查新計算的MAC與從傳送方收到的MAC是否相等。如果匹配，則接收方接受訊息並確保訊息是由預期傳送方傳送的。
如果計算出的MAC與傳送方傳送的MAC不匹配，接收方無法確定是訊息被更改了還是來源被偽造了。底線是，接收方安全地假設該訊息不是真實的。

MAC的侷限性

MAC有兩個主要侷限性，這兩個侷限性都是由於其對稱操作的性質：

共享金鑰的建立。
- 它可以在擁有共享金鑰的預先確定的合法使用者之間提供訊息認證。
- 這需要在使用MAC之前建立共享金鑰。
無法提供不可否認性
- 不可否認性是指確保訊息傳送者無法否認其先前傳送的任何訊息、承諾或行為。
- 訊息認證碼 (MAC) 技術不提供不可否認性服務。如果傳送方和接收方就訊息來源發生爭議，MAC 無法提供證明訊息確實由傳送方傳送的證據。
- 儘管任何第三方都無法計算 MAC，但傳送方仍可能否認已傳送訊息，並聲稱接收方偽造了訊息，因為無法確定這兩方中哪一方計算了 MAC。

可以使用下一節中討論的基於公鑰的數字簽名來克服這兩個限制。

密碼學數字簽名

數字簽名是訊息認證的公鑰原語。在現實世界中，通常會在手寫或列印的訊息上使用手寫簽名。它們用於將簽名者繫結到訊息。

類似地，數字簽名是一種將個人/實體繫結到數字資料的方法。接收方以及任何第三方都可以獨立驗證此繫結。

數字簽名是從資料和僅簽名者知道的私鑰計算出的密碼值。

在現實世界中，訊息接收者需要確保訊息屬於傳送者，並且傳送者不應能夠否認該訊息的來源。此要求在業務應用程式中非常重要，因為交換資料發生爭議的可能性非常高。

數字簽名模型

如前所述，數字簽名方案基於公鑰密碼學。數字簽名方案的模型如下圖所示：

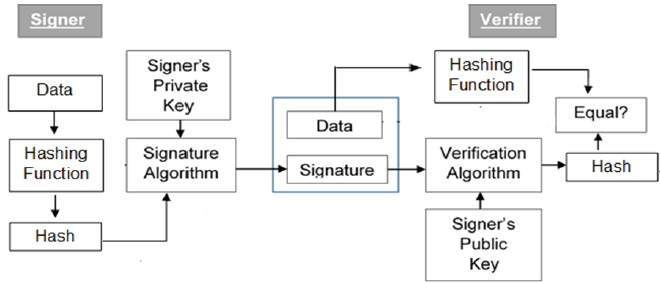
以下幾點詳細解釋了整個過程：

採用此方案的每個人都有一對公鑰和私鑰。
通常，用於加密/解密和簽名/驗證的金鑰對是不同的。用於簽名的私鑰稱為簽名金鑰，公鑰稱為驗證金鑰。
簽名者將資料饋送到雜湊函式並生成資料的雜湊值。
然後將雜湊值和簽名金鑰饋送到簽名演算法，該演算法會生成給定雜湊值的數字簽名。簽名附加到資料中，然後兩者都發送給驗證者。
驗證者將數字簽名和驗證金鑰輸入驗證演算法。驗證演算法會輸出某個值。
驗證者還會對接收到的資料執行相同的雜湊函式以生成雜湊值。
為了驗證，將此雜湊值和驗證演算法的輸出進行比較。根據比較結果，驗證者確定數字簽名是否有效。
由於數字簽名是由簽名者的“私鑰”建立的，並且沒有人擁有此金鑰；簽名者將來無法否認已簽名資料。

需要注意的是，通常不是直接透過簽名演算法對資料進行簽名，而是建立資料的雜湊值。由於資料的雜湊值是資料的唯一表示，因此對雜湊值進行簽名足以代替對資料進行簽名。使用雜湊值而不是直接對資料進行簽名的最重要原因是方案的效率。

讓我們假設 RSA 用作簽名演算法。如公鑰加密章節所述，使用 RSA 的加密/簽名過程涉及模冪運算。

透過模冪運算對大型資料進行簽名在計算上代價高昂且耗時。資料的雜湊值是資料的相對較小的摘要，因此**對雜湊值進行簽名比對整個資料進行簽名更有效**。

數字簽名的重要性

在所有密碼原語中，使用公鑰密碼學的數字簽名被認為是實現資訊安全非常重要和有用的工具。

除了能夠提供訊息的不可否認性外，數字簽名還提供訊息認證和資料完整性。讓我們簡要了解數字簽名是如何實現這一點的：

**訊息認證** - 當驗證者使用傳送者的公鑰驗證數字簽名時，他可以確保簽名僅由擁有相應私鑰的傳送者建立，而不是其他人。
**資料完整性** - 如果攻擊者可以訪問資料並修改資料，則接收端處的數字簽名驗證將失敗。修改後資料的雜湊值和驗證演算法提供的輸出將不匹配。因此，接收者可以安全地否認該訊息，並假設資料完整性已被破壞。
**不可否認性** - 由於假定只有簽名者知道簽名金鑰，因此他只能對給定資料建立唯一的簽名。因此，如果將來發生任何爭議，接收者可以向第三方出示資料和數字簽名作為證據。

透過向數字簽名方案新增公鑰加密，我們可以建立一個能夠提供四個基本安全要素的密碼系統，即：隱私、身份驗證、完整性和不可否認性。

帶有數字簽名的加密

在許多數字通訊中，交換加密訊息而不是明文以實現機密性是可取的。在公鑰加密方案中，傳送者的公鑰（加密金鑰）在公共領域可用，因此任何人都可以偽造其身份並將任何加密訊息傳送給接收者。

這使得使用 PKC 進行加密的使用者必須尋求數字簽名以及加密資料，以確保訊息認證和不可否認性。

這可以透過將數字簽名與加密方案相結合來實現。讓我們簡要討論如何實現此要求。有**兩種可能性：先簽名後加密**和**先加密後簽名**。

但是，基於先簽名後加密的密碼系統可以被接收者利用來偽造傳送者的身份並將資料傳送給第三方。因此，這種方法不被推薦。先加密後簽名的過程更可靠且被廣泛採用。如下圖所示：

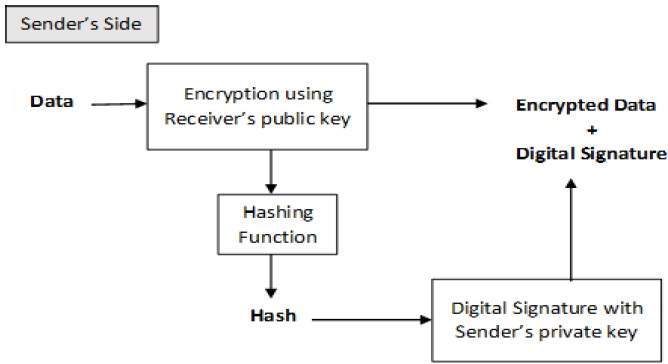
接收者在接收加密資料及其簽名後，首先使用傳送者的公鑰驗證簽名。在確保簽名的有效性後，他然後使用其私鑰透過解密檢索資料。

公鑰基礎設施 (PKI)

公鑰基礎設施 (PKI) 最顯著的特點是它使用一對金鑰來實現底層安全服務。金鑰對包括私鑰和公鑰。

由於公鑰在公共領域，因此它們很可能被濫用。因此，有必要建立和維護某種可信賴的基礎設施來管理這些金鑰。

金鑰管理

不用說，任何密碼系統的安全性都取決於其金鑰的安全性如何管理。如果沒有安全的密碼金鑰處理程式，使用強大密碼方案的好處可能會丟失。

據觀察，密碼方案很少因其設計中的弱點而受到破壞。但是，它們通常由於金鑰管理不善而受到破壞。

金鑰管理有一些重要的方面，如下所示：

密碼金鑰只不過是特殊的資料片段。金鑰管理是指對密碼金鑰的安全管理。
金鑰管理處理整個金鑰生命週期，如下圖所示：

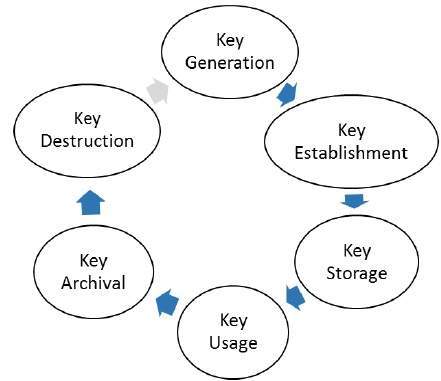
公鑰密碼學的金鑰管理有兩個具體要求。
- **私鑰的保密性。**在整個金鑰生命週期中，秘密金鑰必須對除所有者和授權使用它們的方以外的所有方保密。
- **公鑰的保證。**在公鑰密碼學中，公鑰在公共領域，被視為公共資料。預設情況下，無法保證公鑰是否正確，可以與誰關聯，或可以用於什麼目的。因此，公鑰的金鑰管理需要更明確地關注公鑰目的的保證。

“公鑰保證”的最重要要求可以透過公鑰基礎設施 (PKI) 來實現，這是一種支援公鑰密碼學的金鑰管理系統。

公鑰基礎設施 (PKI)

PKI 提供公鑰保證。它提供公鑰的身份驗證和分發。PKI 的結構包括以下元件。

公鑰證書，通常稱為“數字證書”。
私鑰令牌。
認證機構。
註冊機構。
證書管理系統。

數字證書

作為類比，證書可以被認為是簽發給個人的身份證。人們使用身份證，例如駕駛執照、護照來證明自己的身份。數字證書在電子世界中做同樣的事情，但有一點不同。

數字證書不僅簽發給個人，還可以簽發給計算機、軟體包或任何其他需要在電子世界中證明身份的任何東西。

數字證書基於 ITU 標準 X.509，該標準定義了公鑰證書和證書驗證的標準證書格式。因此，數字證書有時也稱為 X.509 證書。

屬於使用者客戶端的公鑰由認證機構 (CA) 儲存在數字證書中，以及其他相關資訊，例如客戶端資訊、到期日期、用途、發行者等。
CA 對所有這些資訊進行數字簽名，並將數字簽名包含在證書中。
任何需要關於客戶端公鑰和關聯資訊保證的人，都可以使用 CA 的公鑰執行簽名驗證過程。成功驗證確保證書中提供的公鑰屬於證書中提供的詳細資訊的人。

個人/實體獲取數字證書的過程如下圖所示。

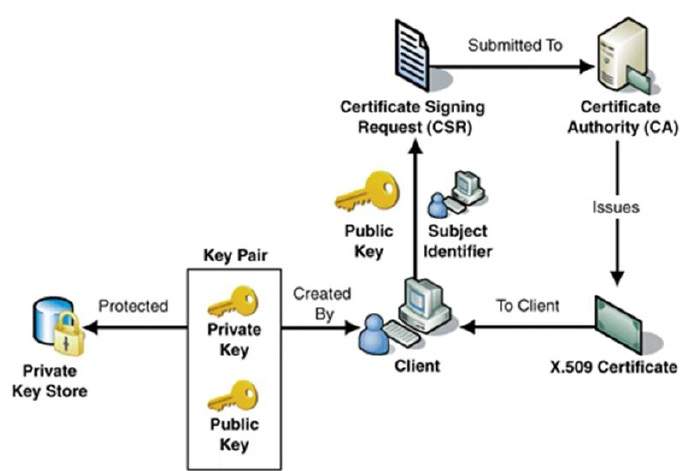
如插圖所示，CA 接受客戶端的申請以認證其公鑰。CA 在適當驗證客戶端身份後，向該客戶端頒發數字證書。

認證機構 (CA)

如上所述，CA 向客戶端頒發證書，並幫助其他使用者驗證證書。CA 負責正確識別請求頒發證書的客戶端身份，並確保證書中包含的資訊正確無誤，並對其進行數字簽名。

CA 的關鍵功能

CA 的關鍵功能如下：

生成金鑰對 – CA 可以獨立或與客戶端聯合生成金鑰對。
頒發數字證書 – 可以將 CA 視為 PKI 等效於護照機構 – CA 在客戶端提供憑據以確認其身份後頒發證書。然後，CA 對證書進行簽名以防止修改證書中包含的詳細資訊。
釋出證書 – CA 需要釋出證書以便使用者可以找到它們。實現這一點有兩種方法。一種是在相當於電子電話簿中釋出證書。另一種是透過某種方式將您的證書傳送給您認為可能需要它的那些人。
驗證證書 – CA 將其公鑰提供給環境，以幫助驗證其在客戶端數字證書上的簽名。
吊銷證書 – 有時，CA 會由於某些原因吊銷已頒發的證書，例如使用者私鑰洩露或對客戶端失去信任。吊銷後，CA 會維護所有已吊銷證書的列表，該列表可供環境使用。

證書類別

共有四類典型的證書：

第 1 類 – 透過提供電子郵件地址即可輕鬆獲取這些證書。
第 2 類 – 這些證書需要提供額外的個人資訊。
第 3 類 – 只有在對請求者的身份進行檢查後才能購買這些證書。
第 4 類 – 這些證書可由需要極高信任級別的政府和金融機構使用。

註冊機構 (RA)

CA 可以使用第三方註冊機構 (RA) 來對請求證書的個人或公司進行必要的檢查以確認其身份。RA 可能會在客戶端看來像 CA，但他們實際上並沒有簽署頒發的證書。

證書管理系統 (CMS)

這是一個管理系統，透過該系統可以釋出、暫時或永久吊銷、續訂或吊銷證書。證書管理系統通常不刪除證書，因為可能需要在某個時間點證明其狀態，也許出於法律原因。CA 以及相關的 RA 執行證書管理系統，以便能夠跟蹤其責任和義務。

私鑰令牌

雖然客戶端的公鑰儲存在證書上，但相關的私鑰可以儲存在金鑰所有者的計算機上。這種方法通常不被採用。如果攻擊者訪問了計算機，他可以輕鬆訪問私鑰。為此，私鑰儲存在安全的可移動儲存令牌上，對該令牌的訪問透過密碼進行保護。

不同的供應商通常使用不同且有時是專有的金鑰儲存格式。例如，Entrust 使用專有的 .epf 格式，而 Verisign、GlobalSign 和 Baltimore 使用標準的 .p12 格式。

CA 的層次結構

隨著龐大的網路和全球通訊的需求，實際上不可能只有一個可信的 CA，所有使用者都從該 CA 獲取證書。其次，如果 CA 被破壞，只有一個 CA 的可用性可能會導致困難。

在這種情況下，分層證書模型非常重要，因為它允許在兩個通訊方與同一 CA 沒有信任關係的環境中使用公鑰證書。

根 CA 位於 CA 層次結構的頂部，根 CA 的證書是自簽名證書。
直接隸屬於根 CA 的 CA（例如，CA1 和 CA2）具有由根 CA 簽名的 CA 證書。
層次結構中從屬 CA 下的 CA（例如，CA5 和 CA6）的 CA 證書由更高級別的從屬 CA 簽名。

證書頒發機構 (CA) 層次結構反映在證書鏈中。證書鏈跟蹤從層次結構中的分支到層次結構根的證書路徑。

下圖顯示了一個 CA 層次結構，其中證書鏈從實體證書透過兩個從屬 CA 證書 (CA6 和 CA3) 到根 CA 的 CA 證書。

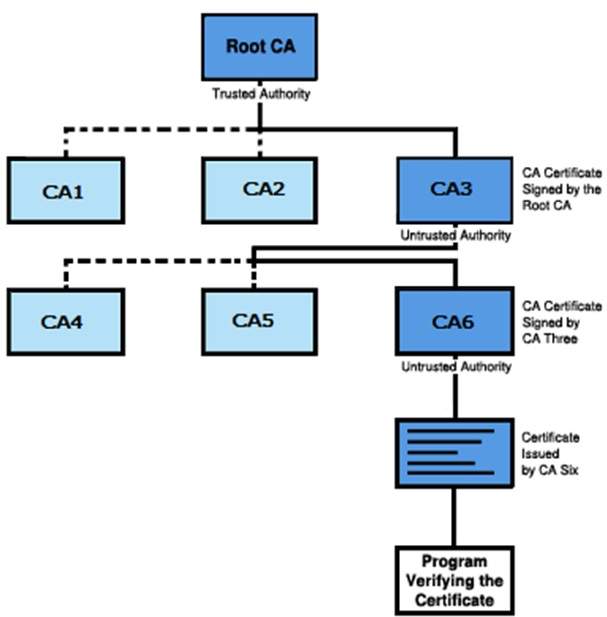
驗證證書鏈是確保特定證書鏈有效、正確簽名且值得信賴的過程。以下過程驗證證書鏈，從為身份驗證提供的證書開始：

正在驗證其真實性的客戶端提供其證書，通常還提供證書鏈直至根 CA。
驗證者獲取證書並使用發行者的公鑰進行驗證。發行者的公鑰位於緊鄰客戶端證書的鏈中的發行者證書中。
現在，如果已簽署發行者證書的更高 CA 受驗證者信任，則驗證成功並在此處停止。
否則，將以與上述步驟中客戶端類似的方式驗證發行者證書。此過程一直持續到找到受信任的 CA，或者持續到根 CA。

密碼學 - 優點與缺點

如今，網路已走向全球，資訊已採用位和位元組的數字形式。關鍵資訊現在以數字形式儲存、處理和傳輸到計算機系統和開放通訊通道上。

由於資訊扮演著如此重要的角色，對手的目標是計算機系統和開放通訊通道，目的是竊取敏感資訊或破壞關鍵資訊系統。

現代密碼學提供了一套強大的技術，以確保挫敗對手的惡意意圖，同時確保合法使用者能夠訪問資訊。在本章中，我們將討論我們從密碼學中獲得的好處、其侷限性以及密碼學的未來。

密碼學 – 好處

密碼學是必不可少的安全工具。它提供了資訊安全四個最基本的服務：

機密性 – 加密技術可以保護資訊和通訊免受未經授權的洩露和訪問。
身份驗證 – MAC 和數字簽名等密碼技術可以保護資訊免受欺騙和偽造。
資料完整性 – 密碼雜湊函式在確保使用者資料完整性方面發揮著至關重要的作用。
不可否認性 – 數字簽名提供不可否認性服務，以防止因傳送者否認傳遞訊息而產生的爭議。

密碼學提供的所有這些基本服務使得能夠以極其高效和有效的方式透過使用計算機系統的網路進行業務活動。

密碼學 – 缺點

除了資訊安全的四個基本要素之外，還有一些其他問題會影響資訊的有效使用：

在關鍵的決策時刻，即使對於合法使用者而言，強加密、身份驗證和數字簽名的資訊也可能難以訪問。網路或計算機系統可能會受到攻擊，並被入侵者破壞功能。
資訊安全的另一個基本方面高可用性無法透過使用密碼學來保證。需要其他方法來防範諸如拒絕服務或資訊系統完全崩潰之類的威脅。
資訊安全的另一個基本需求選擇性訪問控制也不能透過使用密碼學來實現。需要為此執行管理控制和程式。
密碼學不能防範系統、協議和程式設計不當而產生的漏洞和威脅。需要透過適當的設計和防禦基礎設施的設定來解決這些問題。
密碼學是有成本的。成本以時間和金錢來衡量：
- 在資訊處理中新增密碼技術會導致延遲。
- 使用公鑰密碼需要建立和維護公鑰基礎設施，這需要大量的資金預算。
密碼技術的安全性基於數學問題的計算難度。解決此類數學問題的任何突破或計算能力的提高都可能使密碼技術變得脆弱。

密碼學的未來

橢圓曲線密碼學 (ECC) 已經被髮明，但其優點和缺點尚未完全瞭解。ECC 允許以極短的時間執行加密和解密，從而允許在安全性相同的情況下傳遞更多的資料。但是，與其他加密方法一樣，ECC 也必須經過測試並證明其安全可靠後才能被政府、商業和私人使用所接受。

量子計算是一種新現象。雖然現代計算機使用稱為“位”的二進位制格式儲存資料，其中可以儲存“1”或“0”；量子計算機使用多個狀態的量子疊加儲存資料。這些多值狀態儲存在“量子位”或“量子位元”中。這允許以比傳統的電晶體處理器快幾個數量級的速度計算數字。

要理解量子計算機的強大功能，請考慮 RSA-640，這是一個具有 193 位數字的數字，可以透過 80 臺 2.2GHz 計算機在 5 個月內進行因式分解，一臺量子計算機可以在不到 17 秒的時間內進行因式分解。對於傳統計算機來說通常需要數十億年才能計算的數字，對於完全開發的量子計算機來說，可能只需要幾小時甚至幾分鐘的時間。

鑑於這些事實，現代密碼學必須尋找計算難度更大的問題，或者設計完全存檔當前現代密碼學所實現目標的新技術。

列印頁面