密碼學 - 一次性密碼本密碼

---

---

一次性密碼本演算法是維吉尼亞密碼的增強版本。它是唯一已知的不可破解的加密方法，提供完全的安全性。此演算法使用替換技術對字母文字進行加密，為明文中的每個字元分配數字。

要有效地使用一次性密碼本，必須滿足三個條件

• 加密金鑰的長度與秘密訊息的長度匹配。

• 加密金鑰僅由隨機生成的符號組成。

• 每個加密金鑰僅使用一次，並且永遠不會重複用於多條訊息。

在一次性密碼本加密系統中，每條訊息都使用與訊息一樣長的唯一金鑰進行加密。加密的訊息（稱為密文）看起來像是完全隨機的，與原始訊息（稱為明文）沒有相似之處。這使得在沒有正確金鑰的情況下很難破譯。

一次性密碼本如何工作？

一次性密碼本涉及建立一系列字元或數字，其長度等於或長於預期的最長訊息。此序列是隨機生成的，通常使用具有隨機數生成器的計算機程式。這些值以物理方式記錄在便箋簿或可讀裝置上。便箋簿分發給可能交換敏感訊息的個人。它們可以作為多個金鑰分發，每個金鑰分配給特定的一天或特定數量的使用次數，確保每個金鑰僅使用一次，然後丟棄。

傳送訊息時，傳送方使用秘密金鑰逐字元對其進行加密。使用計算機，字元中的每個位元（通常為 8 個位元）與金鑰中的相應位元使用 XOR 運算組合。在一次性密碼本系統中，XOR 是加密方法。如果金鑰的隨機性不確定，則可以將其與 MD5 等演算法結合使用。這種型別的加密就像向訊息中新增隨機噪聲一樣，只有傳送方和接收方有辦法去除噪聲。一次性密碼本僅使用一次，並且不得重複使用。重複使用便箋簿會使攔截者能夠比較訊息並可能破譯它們。

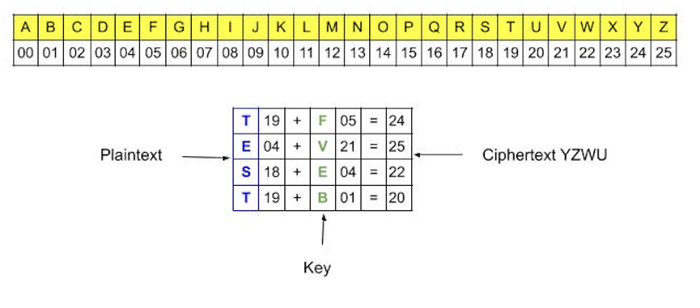
為了說明一次性密碼本的工作原理，請考慮訊息“TEST”。生成長度相等的一組秘密金鑰“FVEB”。每個字母都分配一個數字，TEST：19、4、18、19 和 FVEB：5、21、4、1。新增與明文和金鑰相對應的數字：24、25、22、20。將這些數字轉換回字母：加密訊息：YZWU 要解密，只需反轉該過程即可，即可顯示原始訊息“TEST”。

為什麼一次性密碼本是不可破解的？

一次性密碼本 (OTP) 的不可破解性被認為是不可破解的，因為與可以透過模式分析破解的維吉尼亞密碼不同，OTP 金鑰與訊息本身一樣長。每個可能的加密符號都有相同的機率表示相同的原始符號，這使得頻率分析在揭示正確訊息方面無效。

使用的金鑰完全隨機且與訊息長度匹配，消除了駭客可以利用的任何可預測的模式。每個訊息交換後都會丟棄金鑰。沒有它，即使是傳送方和接收方也無法破譯訊息。因為金鑰是隨機的並且僅使用一次，所以它不會留下駭客可以猜測以破解程式碼的任何提示或模式。

一次性密碼本加密

假設使用者 1 想向用戶 2 傳送一條私人訊息。使用者 1 寫下“HELLO”並建立一個唯一金鑰“QWERT”。-

• 為了保密，使用者 1 將“HELLO”的每個字母與“QWERT”中的相應字母匹配。例如，H = A + Q，E = B + W。

• 使用者 1 的加密訊息變為“QGNNQ”。

• 使用者 2 收到加密訊息並使用相同的“QWERT”金鑰對其進行解碼。

• 他反轉規則：H - A = Q，E - W = G。

• 使用者 2 恢復原始訊息“HELLO”。

由於金鑰僅使用一次且完全不可預測，因此任何攔截加密訊息的人在沒有金鑰的情況下都無法對其進行破譯。這就是一次性密碼本被認為是不可破解的原因。

一次性密碼本解密

要使用一次性密碼本解密訊息，請按照以下步驟操作 -

• 收集加密的訊息和加密金鑰。

• 反轉加密過程中執行的操作：- 如果添加了字母，則減去它們。

• 使用解密金鑰對每個字母應用反向操作。

• 透過反轉所有轉換來獲取原始的解密訊息。

示例

要使用金鑰“WORLD”解密“QKRRU”：- 從“Q”中減去“W”得到“H”。- 從“K”中減去“O”得到“E”。- 對所有字母繼續此過程。- 生成的訊息“HELLO”是解密的明文。

優點

以下是一次性密碼本密碼的一些優點，我們在使用此密碼時應考慮 -

• 一次性密碼本加密透過使用保密且僅使用一次的金鑰提供儘可能強的保護。

• 與其他加密技術不同，它不受諸如暴力破解或已知明文攻擊等弱點的影響。

• 一次性密碼本加密可以輕鬆適應文字資料和二進位制資料。

• 它的實現很簡單，允許手動執行或在計算機的支援下執行。

OTP 的用例

請參見下面一次性密碼的用例 -

• 關鍵通訊 - 軍事和政府行動所需的至關重要的通訊，需要最高的安全性。

• 外交保密 - 最高官員、外交官和情報機構之間的安全通訊。

• 商業機密 − 保護敏感的財務和商業資訊免受競爭對手的侵害。

• 個人隱私 − 保護私人和機密資訊，包括醫療記錄和法律檔案。

缺點

雖然 OTP 在正確使用時提供牢不可破的安全性，但其在金鑰管理和分發方面的實際限制和挑戰使其在許多現實世界應用中相比其他加密方法不太適用。

總結

一次性密碼密碼透過為每條訊息使用唯一的金鑰來提供高安全性，這使得未經授權的方在沒有相關金鑰的情況下無法解密加密資料。加密和解密過程可以透過各種方法實現，例如模運算、加減法、異或運算或利用 Python 的 onetimepad 模組。

加密和解密過程均保證轉換後的字元保持在允許的 ASCII 值範圍內，從而實現準確的反向轉換。