密碼學 - 傳統密碼

---

---

傳統密碼以只有擁有金鑰的人才能解碼的方式對訊息進行編碼。縱觀歷史，它一直被用於私人通訊。

在現代計算機加密技術出現之前，這些密碼被廣泛使用。雖然相對簡單，但如果使用得當，它也可以非常有效，並提供對加密歷史的有趣見解。

以下是一些常見的型別：

• 凱撒密碼

• 維吉尼亞密碼

• 簡單替換密碼

• 單表代換密碼和多表代換密碼

• 轉置密碼

• Playfair密碼

早期密碼系統

在繼續之前，您應該瞭解有關密碼系統的一些事實：

• 這些系統都是使用對稱金鑰加密構建的。

• 這些系統僅將資訊機密性作為安全特性。

• 與將資料作為二進位制數字處理的現代數字系統相比，以前的系統使用字母作為基本構建塊。

這些早期的密碼方案也稱為密碼。一般來說，密碼只是可以用來執行加密以及相應解密的步驟（演算法）。

現在讓我們逐一討論上述傳統密碼型別。

凱撒密碼

凱撒密碼是一種替換密碼，其中給定明文中每個字母都沿字母表向上或向下移動一定數量的位置。移位數稱為金鑰。它由尤利烏斯·凱撒建立。據信，這種密碼是為了與他的將軍秘密溝通。

對於這種方法，傳送方和接收方都應該就用於移動給定明文字母表的“秘密移位金鑰”達成一致。介於 0 和 25 之間的數字是加密金鑰。

當使用“移位 3”時，此技術有時用於描述移位密碼。

例如 - 如果明文移位 4

• “A”將變為“E”

• “B”將變為“F”

• “C”將變為“G”

• 等等…

凱撒密碼是一種非常簡單易懂的加密方法。但它也很容易破解，因為只有 25 個可能的金鑰，使用暴力破解很容易猜到。

維吉尼亞密碼

維吉尼亞密碼也是一種傳統的密碼演算法，它使用文字字串（例如一個單詞）作為金鑰。然後將其用於對給定明文進行多次移位。

例如：假設金鑰是“tutor”。在此，金鑰的每個字母都更改為其相應的數值：在本例中，

t → 20，u → 21，t → 20，o → 15，r → 18。

因此，金鑰為：20 21 20 15 18。

維吉尼亞密碼步驟

首先，傳送方和接收方確定一個金鑰。假設金鑰是“tutor”。因此，“20 21 20 15 18”是此金鑰的數字表示。

現在，傳送方將加密訊息。訊息是“This is ethical hacker”。然後它將按如下所示排列為數字金鑰：

現在，我們將使用下面字母下方的數字來移動每個明文字母。

在上圖中，明文的每個字母都移動了不同的數量，並且該數量由金鑰確定。金鑰應小於或等於訊息的大小。

在解密過程中，接收方將使用相同的金鑰並將接收到的密文按相反的順序移動以獲得明文。

維吉尼亞密碼旨在調整標準凱撒密碼以降低對密文的密碼分析效率並提高密碼系統的魯棒性。它比普通的凱撒密碼安全得多。

縱觀歷史，它經常被用來保護重要的政治和軍事資訊。由於難以分割秘密，它被稱為不可破的密碼。

維吉尼亞密碼有兩個要點：

關鍵字的長度與明文訊息相同。這種說法稱為 varnam 密碼。這比標準的維吉尼亞密碼更安全。維吉尼亞密碼將是一個具有完全隱私的密碼系統，稱為一次性密碼本。

簡單替換密碼

簡單替換密碼是一種加密形式，其中明文中的字母根據固定的順序被替換為密文中另一個字元。換句話說，它是一種編碼方法，任何字母和字元都被對映到其他字元。

例如，在簡單替換密碼中：

• ’A’ 可以被替換為 ’X’

• ’B’ 可以被替換為 ’K’

• ’C’ 可以被替換為 ’Q’

• 以此類推……直到字母表中的每個字元都被替換為另一個字元。

解密訊息的關鍵在於知道所使用的替換模型。這些密碼相對易於使用，但可以透過頻率分析來破解，這需要分析密文中字元的頻率並去除對映關係。

簡單的替代密碼比凱撒密碼有了很大的改進。可能的金鑰數量非常龐大（26！）即使是現代計算機系統也無法輕鬆地執行暴力破解攻擊來破解該系統。然而，簡單的替代密碼具有簡單且常見的結構系統缺陷，例如選擇明顯的替換。

單表代換密碼和多表代換密碼

單字母替換密碼是一種替換密碼，其中固定字元始終被替換為密文中對應的字元，這意味著明文中的每個字元始終被替換為密文中相同的對應字元。在整個加密過程中，替換保持不變。

例如，如果在加密過程中’A’被替換為’E’，則明文中任何出現的’A’都將被替換為密文中的’E’，如果’B’被替換為’F’，則將明文中任何’B’替換為密文中的’F’。

多字母替換密碼是一種替換密碼，其中明文字元被替換為密文字元，而替換方式隨著加密過程而變化。這意味著明文字元可以被替換為密文字元，具體取決於加密金鑰和字元在明文中的位置。

最流行的多字母替換密碼是維吉尼亞密碼，其中加密金鑰決定字母在密文中出現的位置。與單字母替換密碼不同，多字母替換密碼更安全，因為它們引入了加密方案的變化，使得頻率分析和其他攻擊更加困難。

轉置密碼

這是一種新型密碼，其中明文中的字母序列被重新排列以建立密文。它們並沒有被實際的明文替換。

一個例子是簡單的列置換密碼，其中明文以特定的字母寬度寫入。然後直接按指示讀取密文。

例如，明文是“The tajmahal is in agra”，隨機選擇的隱藏金鑰是“Four”。我們將此文字直接格式化為一個表格，其中包含金鑰值的列數。生成的文字如下所示。

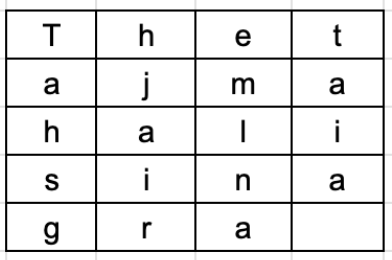
現在，我們可以透過垂直向下從第一列到最後一列讀取來獲得密文。密文將是'Tahsghjairemlnataia'。

Playfair密碼

Playfair 密碼使用 5x5 的字母網格（除非是雙字母，通常用 'J' 代替）進行加密。訊息透過配對字母並使用規則進行加密：如果在同一行，則向右轉；如果在同一列，則向下轉；如果在不同行和列，則構成一個矩形並用對角線上的字母替換。解密遵循相反的規則。Playfair 加密字元對，使其比單字元密碼更安全，但仍然容易受到攻擊。