自定義構建密碼演算法（混合密碼學）

上一頁
下一頁

混合密碼學結合了兩種或多種加密技術。它結合了非對稱加密和對稱加密，以利用各自的功能。該方案使用公鑰密碼學來共享金鑰，並使用對稱加密來高效地加密訊息。

混合加密方案結合了非對稱加密方法的優點和對稱加密方法的有效性。

要加密訊息，首先生成一個對稱金鑰。然後，想要向其傳送訊息的人共享她的公鑰，同時保持私鑰私密。之後，使用接收者的公鑰加密對稱金鑰並將其傳輸給他們。

要解密通訊，接收者使用她的私鑰解密加密的對稱金鑰以獲得解密金鑰，然後她使用該金鑰來解碼訊息。

檢視下面的圖片以直觀地瞭解混合密碼學

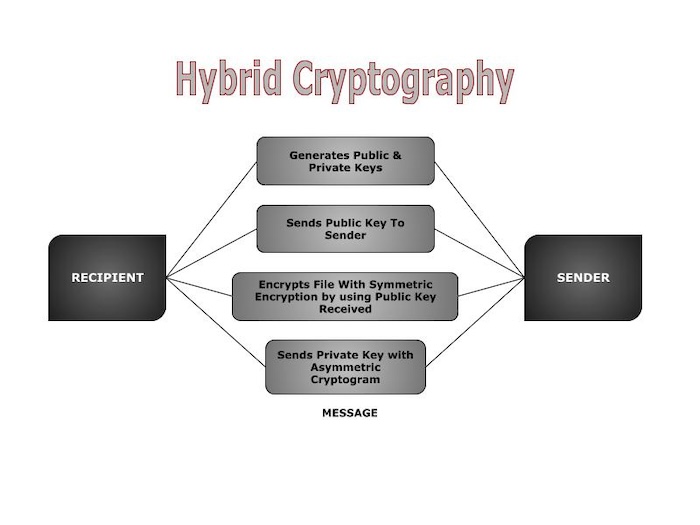
Hybrid Cryptography

以下是我們在上圖中提到的步驟的解釋：

  • 生成公鑰和私鑰 - 接收者首先建立一對金鑰：公鑰和私鑰。
  • 將公鑰傳送給傳送者 - 接收者將其公鑰傳送給傳送者。公鑰可以公開分發，因為它僅用於加密。
  • 使用接收到的公鑰透過對稱加密加密檔案 - 傳送者希望安全地將檔案傳送給接收者。傳送者在使用對稱加密加密檔案的同時，也使用了接收者的公鑰。這意味著只有擁有相應私鑰的接收者才能解密檔案。
  • 使用非對稱密碼傳送私鑰 - 傳送者現在將把接收者的私鑰傳送給他，但它是使用非對稱加密加密的。此加密的私鑰確保只有擁有相應私鑰的預期接收者才能解密它。

混合密碼學的實現

我們將藉助不同的程式語言（如 Python、Java 和 C++）來實現混合密碼學。因此，請參考以下部分的程式碼：

使用 Python

此實現中的自定義加密基於移動連線金鑰中每個字元的 ASCII 值。對於偶數索引的字元，每個字元都按公鑰的長度移動，對於奇數索引的字元，每個字元都按對稱金鑰的長度移動。這是一種簡單的加密型別，它仍然使用組合金鑰和應用自定義轉換的方法。因此，請參見下面的 Python 實現：

def hybrid_encrypt(message, public_key, symmetric_key):
   # Reverse the message
   reversed_message = message[::-1]
   # Combine reversed message with symmetric key
   combined_key = reversed_message + symmetric_key

   # change combined key to list of characters
   key_characters = list(combined_key)

   # Apply custom encryption
   encrypted_characters = []
   for i, char in enumerate(key_characters):
      if i % 2 == 0:
         encrypted_char = chr(ord(char) + len(public_key))  # Shift ASCII value by length of public key
      else:
         encrypted_char = chr(ord(char) - len(symmetric_key))  # Shift ASCII value by length of symmetric key
         encrypted_characters.append(encrypted_char)

   # Combine encrypted characters 
   encrypted_message = ''.join(encrypted_characters)

   return encrypted_message

# our message, public key and symmetric key
message = "hellotutorialspoint"
public_key = "qwer"
symmetric_key = "private"

# function execution

encrypted_message = hybrid_encrypt(message, public_key, symmetric_key)
print("Our Encrypted Message:", encrypted_message)

輸出

Our Encrypted Message: xgmhtlpZmksmymsep^livbzZx^

使用 Java

此 Java 程式演示了使用給定金鑰對明文訊息應用的混合加密技術。main 方法初始化明文訊息和金鑰，然後呼叫 encryptMessage 函式來加密明文。

import java.util.*;

class HybridEncryption {

   public static void main(String[] args) {
      String plaintext = "hellotutorialspoint";
      String key = "qwer";
      System.out.println("Our Encrypted Message is: " + encryptMessage(plaintext, key));
   }

   public static String encryptMessage(String message, String key) {
      int a = 0, b = 1, c = 0, m = 0, k = 0, j = 0;
      String encryptedText = "", temp = "";

      // Reverse the message
      StringBuilder reversedMessage = new StringBuilder(message).reverse();
      // Combine the reversed message with the key
      StringBuilder combinedString = reversedMessage.append(key);

      // change the combined string to a character array
      char[] charArray = combinedString.toString().toCharArray();
      String evenChars = "", oddChars = "";

      // Separate characters into even and odd positions
      for (int i = 0; i < charArray.length; i++) {
         if (i % 2 == 0) {
            oddChars += charArray[i];
         }else {
            evenChars += charArray[i];
         }
      }

      char[] evenArray = new char[evenChars.length()];
      char[] oddArray = new char[oddChars.length()];

      // create a Fibonacci series and apply Caesar cipher
      while (m <= key.length()) {
         if (m == 0)
            m = 1;
         else {
            a = b;
            b = c;
            c = a + b;
            for (int i = 0; i < evenChars.length(); i++) {
               int p = evenChars.charAt(i);
               int cipher = 0;
               if (Character.isDigit(p)) {
                  cipher = p - c;
                  if (cipher < '0')
                     cipher = cipher + 9;
               }else {
                  cipher = p - c;
                  if (cipher < 'a') {
                     cipher = cipher + 26;
                  }
               }
               evenArray[i] = (char)cipher;
            }
            for (int i = 0; i < oddChars.length(); i++) {
               int p = oddChars.charAt(i);
               int cipher = 0;
               if (Character.isDigit(p)) {
                  cipher = p + c;
                  if (cipher > '9')
                     cipher = cipher - 9;
               }else {
                  cipher = p + c;
                  if (cipher > 'z') {
                     cipher = cipher - 26;
                  }
               }
               oddArray[i] = (char)cipher;
            }
            m++;
         }
      }

      // Combine even and odd characters based on their positions
      for (int i = 0; i < charArray.length; i++) {
         if (i % 2 == 0) {
            charArray[i] = oddArray[k];
            k++;
         }else {
            charArray[i] = evenArray[j];
            j++;
         }
      }
      // Generate the encrypted text
      for (char d : charArray) {
         encryptedText = encryptedText + d;
      }

      // Return the encrypted text
      return encryptedText;
   }
}

輸出

Our Encrypted Message is: wkllspoxlorqxqriobknzbu

使用 C++

此 C++ 程式碼顯示了一種自定義加密演算法，該演算法結合了反向字串操作和凱撒密碼來加密訊息。

#include <iostream>
#include <string>
#include <algorithm> // Include the algorithm header for the reverse function

using namespace std;

string hybridEncryption(string password, string key) {
   int a = 0, b = 1, c = 0,
      m = 0, k = 0, j = 0;
   string cipherText = "", temp = "";

   // Declare a password string
   string reversedPassword = password;

   // Reverse the String
   reverse(reversedPassword.begin(), reversedPassword.end()); // Use the reverse function
   reversedPassword = reversedPassword + key;

   // For future Purpose
   temp = reversedPassword;
   string charArray = temp;
   string evenChars = "", oddChars = "";

   // Declare EvenArray for storing
   // even index of charArray
   char *evenArray;

   // Declare OddArray for storing
   // odd index of charArray
   char *oddArray;

   // Storing the positions in their
   // respective arrays
   for (int i = 0; i < charArray.length(); i++) {
      if (i % 2 == 0) {
         oddChars = oddChars + charArray[i];
      }else {
         evenChars = evenChars + charArray[i];
      }
   }

   evenArray = new char[evenChars.length()];
   oddArray = new char[oddChars.length()];

   // Generate a Fibonacci Series
   // Upto the Key Length
   while (m <= key.length()) {

      // As it always starts with 1
      if (m == 0)
         m = 1;

      else {

         // Logic For Fibonacci Series
         a = b;
         b = c;
         c = a + b;

         for (int i = 0; i < charArray.length(); i++) {

            // Caesar Cipher Algorithm Start
            // for even positions
            int p = charArray[i];
            int cipher = 0;

            if (p == '0' || p == '1' ||
               p == '2' || p == '3' ||
               p == '4' || p == '5' ||
               p == '6' || p == '7' ||
               p == '8' || p == '9') {
               cipher = p - c;

               if (cipher < '0')
                  cipher = cipher + 9;
            }else {
               cipher = p - c;
               if (cipher < 'a') {
                  cipher = cipher + 26;
               }
            }
            evenArray[i] = (char)cipher;

            // Caesar Cipher Algorithm End
         }
         for (int i = 0; i < charArray.length(); i++) {

            // Caesar Cipher Algorithm
            // Start for odd positions
            int p = charArray[i];
            int cipher = 0;

            if (p == '0' || p == '1' ||
               p == '2' || p == '3' ||
               p == '4' || p == '5' ||
               p == '6' || p == '7' ||
               p == '8' || p == '9') {
                  cipher = p + c;
                  if (cipher > '9')
                     cipher = cipher - 9;
            }else {
               cipher = p + c;
               if (cipher > 'z') {
                  cipher = cipher - 26;
               }
            }
            oddArray[i] = (char)cipher;

            // Caesar Cipher Algorithm End
         }
         m++;
      }
   }

   // Storing content of even and
   // odd array to the string array
   for (int i = 0; i < charArray.length(); i++) {
      if (i % 2 == 0) {
         charArray[i] = oddArray[k];
         k++;
      }else {
         charArray[i] = evenArray[j];
         j++;
      }
   }

   // Generating a Cipher Text
   // by charArray (Caesar Cipher)
   for (char d : charArray) {
      cipherText = cipherText + d;
   }

   // Return the Cipher Text
   return cipherText;
}

// Driver code
int main() {
   string pass = "hellotutorialspoint";
   string key = "qwer";

   cout <<"Our Encrypted Message is: "<< hybridEncryption(pass, key);

   return 0;
}

輸出

Our Encrypted Message is: wqqklfrlsmvpoidxlfuorlw

混合密碼學的優點

混合加密是對稱加密和非對稱加密的組合，它比以前的方法提供了更高的安全性。資料的傳輸變得安全。在傳輸過程中加密資料可以提供安全優勢，就像所有裝置上都能確保資料安全一樣。

列印頁面
上一頁
下一頁
廣告
© . All rights reserved.