密碼學 - AES 變換函式

---

---

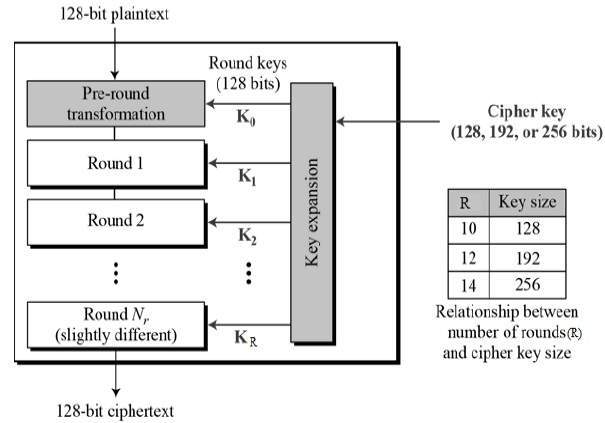
我們現在將逐一介紹 AES 的四個變換。我們將描述正向（加密）演算法、逆向（解密）演算法以及每個步驟的階段原理。

位元組替換變換

AES 加密過程中的主要階段是位元組替換變換，或 SubBytes。現在我們將學習它 -

目的

• SubBytes 變換的目標是使加密過程非線性。
• 使用預先製作的稱為 S 盒的替換表，狀態矩陣中的每個位元組都將更改為一個新位元組。
• 透過引入混淆，這種修改提高了加密過程對密碼分析技術的抵抗力。

S 盒

• S 盒是一個固定的 16x16 矩陣，包含 256 個預定義的位元組值。
• S 盒中每個位元組的值都由特定的數學過程確定。
• S 盒對輸入和輸出位元組的一對一對映允許可逆性。

工作原理？

• 在 SubBytes 變換期間，狀態矩陣中的每個位元組都將更改為與 S 盒中的位元組匹配。
• 狀態矩陣中的每個位元組都將被單獨替換，從而建立一個新的狀態矩陣。
• 透過引入非線性，此替換階段提高了加密過程對包括差分密碼分析在內的各種攻擊的防禦能力。

優點

• SubBytes 破壞了明文中的任何對稱性，這增加了加密的難度。
• 它增加了強加密所需的擴散和混淆特性。
• 當使用預設的 S 盒時，逆 S 盒確保了恆定且可逆的替換方法，這使其可用於解密。

因此，SubBytes 變換對於 AES 加密過程非常重要，因為它提高了加密資料的非線性度和混淆度，從而增強了其安全性。它是著名的 AES 加密方法的一個關鍵組成部分，用於保護私人資訊。

行移位變換

行移位變換是高階加密標準 (AES) 加密過程中的一個重要階段。讓我們看看這個變換的工作原理 -

目的

行移位變換的目的是在狀態矩陣中產生擴散，將每個位元組的影響分佈到整個矩陣。它有助於創造不確定性並提高加密的複雜性，從而提高密文的安全性。

工作原理？

• 在行移位變換期間，狀態矩陣中每一行的位元組都連續向左移動。
• 第三行移動兩個位置，第四行移動三個位置，第二行向左移動一個位置。第一行保持不變。
• 對狀態矩陣中每一行獨立進行的移位操作會產生一個新的狀態矩陣。

示例

假設我們的狀態矩陣是 4x4 -

[a0, a1, a2, a3]
[b0, b1, b2, b3]
[c0, c1, c2, c3]
[d0, d1, d2, d3]

行移位變換後 -

[a0, a1, a2, a3]
[b1, b2, b3, b0]
[c2, c3, c0, c1]
[d3, d0, d1, d2]

優點

• 行移位透過重新排列狀態矩陣中每一行內的位元組，為加密過程增加了擴散。
• 它透過確保狀態矩陣中的每個位元組都會影響後續加密輪次中的多個位元組，從而提高了加密的整體安全性。

行移位變換是 AES 加密過程中的一個關鍵組成部分，它增加了強加密所需的擴散和混淆特性。它對於維護加密資料的安全性至關重要，因為它將每個位元組的影響分佈到整個狀態矩陣。

列混淆變換

列混淆變換是 AES（高階加密標準）加密過程中的另一個步驟。讓我們現在來研究它 -

目的

• 列混淆變換試圖增加擴散並增強加密安全性。
• 它透過將每一列視為有限域上的多項式來對狀態矩陣的列進行操作。
• 列混淆提供了混淆，並使加密過程能夠抵抗各種密碼分析技術。

工作原理？

• 在列混淆變換期間，一個固定的矩陣變換將乘以狀態矩陣的每一列。
• 此變換需要將每一列乘以某個矩陣，然後將輸出模以預定義的多項式。
• 原始狀態矩陣的每一列都將獨立地進行乘法和簡化，以建立一個新的狀態矩陣。

示例

讓我們考慮一個 4x4 矩陣 -

[a0, a1, a2, a3]
[b0, b1, b2, b3]
[c0, c1, c2, c3]
[d0, d1, d2, d3]

列混淆變換後 -

[a0', a1', a2', a3']
[b0', b1', b2', b3']
[c0', c1', c2', c3']
[d0', d1', d2', d3']

優點

• 列混淆透過混合狀態矩陣中每一列的位元組，將擴散引入加密過程。
• 它透過確保狀態矩陣中的每個位元組都會影響後續加密輪次中的多個位元組，從而提高了加密的整體安全性。

列混淆變換是 AES 加密過程的一個組成部分，它增加了強加密所需的擴散和混淆特性。透過混合每個狀態矩陣列中的位元組，它對於維護加密資料的安全性至關重要。

輪金鑰加變換

輪金鑰加變換也是 AES（高階加密標準）加密過程中的一個重要步驟。讓我們仔細研究一下 -

目的

• 輪金鑰加變換將加密金鑰新增到加密過程。
• 由於狀態矩陣和從原始加密金鑰生成的輪金鑰，每一輪加密現在都依賴於明文和加密金鑰。
• 此步驟將金鑰資料整合到加密過程中，以確保生成的密文安全地依賴於明文和金鑰。

工作原理？

• 在輪金鑰加變換期間，狀態矩陣中的每個位元組都將與輪金鑰的相應位元組進行異或運算。
• 原始加密金鑰透過金鑰擴充套件過程來幫助生成每一輪中使用的輪金鑰。
• 對狀態矩陣中的每個位元組執行單獨的異或運算，建立一個新的狀態矩陣。

示例

假設我們有 4x4 的狀態矩陣 -

[a0, a1, a2, a3]
[b0, b1, b2, b3]
[c0, c1, c2, c3]
[d0, d1, d2, d3]

輪金鑰的AddRoundKey變換之後：

[k0, k1, k2, k3]
[k4, k5, k6, k7]
[k8, k9, k10, k11]
[k12, k13, k14, k15]

最終的狀態矩陣如下：

[a0 ⊕ k0, a1 ⊕ k1, a2 ⊕ k2, a3 ⊕ k3]
[b0 ⊕ k4, b1 ⊕ k5, b2 ⊕ k6, b3 ⊕ k7]
[c0 ⊕ k8, c1 ⊕ k9, c2 ⊕ k10, c3 ⊕ k11]
[d0 ⊕ k12, d1 ⊕ k13, d2 ⊕ k14, d3 ⊕ k15]

優點

• AddRoundKey確保明文和加密金鑰對每一輪加密都有影響。
• 使用金鑰材料進行加密增加了額外的保護層，使得攻擊者在沒有金鑰的情況下更難以解密密文。

AddRoundKey變換將金鑰材料包含到加密過程中，並確保生成的密文的安全性，它是AES加密方法的一個重要組成部分。它對於保護個人資訊在移動或儲存過程中的安全至關重要。