密碼學 - 雙重DES

在上一章中，我們瞭解了什麼是資料加密標準，在本章中，我們將詳細瞭解雙重DES。

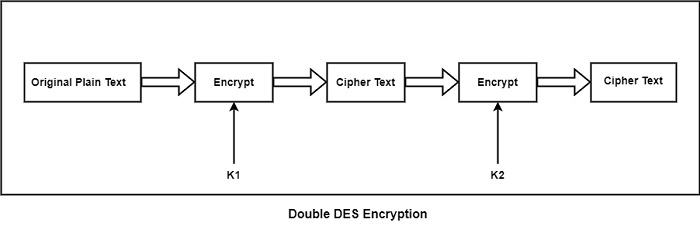
雙重DES是一種加密型別，其中使用一對DES對相同的明文進行加密。在這兩種情況下，都提供了不同的金鑰來加密明文。學習雙重DES很容易。

雙重DES使用兩個金鑰，k1和k2。為了獲得加密文字，它可以使用k1對原始明文應用DES。使用不同的金鑰k2，它可以這次對加密文字應用DES。顯示的加密文字是最終輸出。

雙重DES是如何工作的？

要建立單加密密文，首先使用金鑰K2解密雙加密密文塊。可以透過使用金鑰K1解密此密文塊來檢索原始明文塊。

如果能夠使用單個位元金鑰，則0和1是兩個可用的金鑰。如果可以使用兩個位元金鑰，則有四個可能的金鑰值，例如（00、01、10和11）。

在大多數情況下，如果可以使用n位金鑰，則密碼分析員必須執行2ⁿ次操作才能嘗試所有可能的金鑰。如果可以使用兩個不同的金鑰，每個金鑰都有n位，則密碼分析員將不得不進行2²ⁿ次嘗試來破解金鑰。

將訊息的P（明文塊）和C（相應的最終密文塊）視為密碼分析員知道的兩個基本資訊元素。雙重DES以數字方式表示，如圖所示。

第一次加密的結果稱為T，表示為T = E_k1(P) [即，使用金鑰K1加密塊P]。在使用另一個金鑰K2加密此加密塊後，表示結果為 -

C = E_k2(E_k1(P))

[即，使用不同的金鑰K2加密已經加密的塊T，並將最終密文稱為C]。

雙重DES可以透過稱為中間相遇攻擊的已知明文攻擊來破壞。

給定明文P和兩個加密金鑰K1和K2，密文C產生為C = E_k2(E_k1, (m))解密需要金鑰以相反的順序使用 -

P = D_k1(D_k2, (C))

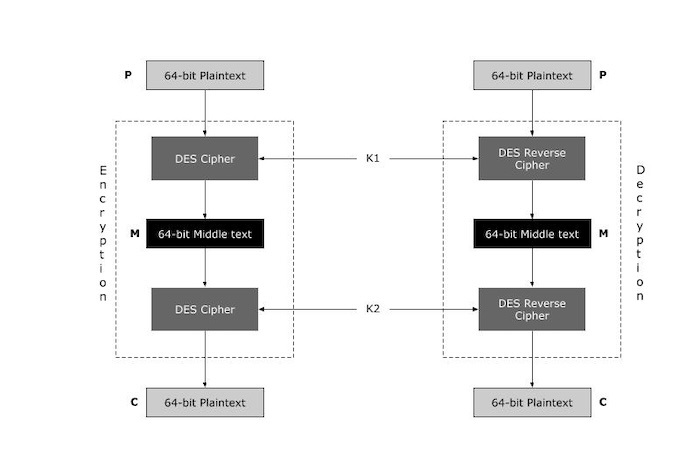
中間相遇 (MitM) 攻擊是一種密碼分析攻擊，攻擊者需要某種型別的空間或時間權衡來支援攻擊。MITM嘗試可以減少執行其原始狀態下攻擊所需的難度。

Merkle 和 Hellman 引入了中間相遇攻擊的概念。這種攻擊包含從一端加密和從另一端解密以及在中間連線結果，因此被稱為中間相遇。

MITM可以建立將目標連線分成兩部分的形式，以便可以獨立地處理每個元素。這可能意味著將需要X時間量的攻擊更改為需要Y時間和Z空間的攻擊。目標是顯著減少執行暴力破解攻擊所需的努力。

中間相遇攻擊者試圖透過在中間相遇或將他們正在分析的區域減半來調和高密碼分析攻擊中包含的難度，以建立在他們看來適用的或合理的努力。

攻擊的主要目的是竊取個人資訊，包括登入憑據、帳戶詳細資訊和信用卡號碼。目標通常是貨幣應用程式、SaaS 業務、電子商務網站和其他需要登入的網站的使用者。

在攻擊期間獲取的資料可用於多種目的，例如身份盜竊、未經授權的資金轉賬或非法更改密碼。

有兩個金鑰，包括K1和K2，用於將明文P加密成密文C，並且類似的K1和K2用於解密。第一次加密和第一次解密產生的中間文字M應該相似，即這兩個關係必須成立。

假設密碼分析員有一個先前的P和C對，那麼它可以使用K1的所有可能值（256）並記錄M的所有值。類似地，對於K2的所有值訪問所有M，從而比較K1和K2的這些M並發現M相同的K1和K2對。

如果只出現一對這樣的對，則K1和K2是所需的金鑰。如果存在多對K1和K2相等的對，則使用另一個攔截的明文/密文對。

雙重DES（資料加密標準）資料加密方法涉及快速執行兩次DES演算法。以下是雙重DES的優點 -

易受中間相遇攻擊 − 雙重DES易受中間相遇攻擊，攻擊者會攔截密文並嘗試第一個加密和解密階段的每個金鑰，同時儲存中間結果。然後，他們嘗試第二個加密階段的每個金鑰，直到找到一個與先前儲存的結果相對應的金鑰。因此，有效金鑰長度減少到112位，大大削弱了理論上的168位金鑰長度。
效能開銷 − 由於雙重DES加密比單重DES加密需要更多時間和計算能力，因此可能會產生效能開銷。
金鑰長度有限 − 雖然雙重DES與單重DES相比將金鑰長度加倍，但它具有相對有限的金鑰長度（計算中間相遇攻擊後為112位有效位）。這可能不足以應對複雜的攻擊，尤其是在計算技術日益強大的情況下。

列印頁面