宇宙學 - 凌日法

---

---

凌日法（開普勒太空望遠鏡）用於確定行星的大小。一顆恆星因行星遮擋而導致的亮度下降通常非常小，不像雙星系統那樣顯著。

• F₀是行星掩食恆星之前恆星的通量。

• F₁是整個行星位於恆星前方後的通量。

下圖將用於所有計算。

$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$

$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$

$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$

$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$

這對於地面望遠鏡來說不容易實現。它是透過哈勃望遠鏡實現的。

這裡，t_T是A點和D點之間的時間，t_F是B點和C點之間的時間。

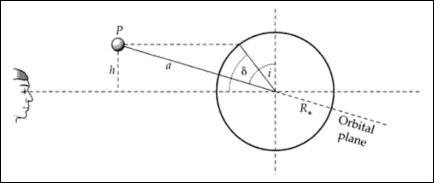
凌日幾何與系統的傾角i有關。凌日緯度和傾角是可以互換的。

從上圖可以看出：

$$\frac{h}{a} = cos(i)$$

$$\frac{h}{R_\ast} = sin(\delta)$$

$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$

$$y^2 = (R_\ast + R_p)^2 - h^2$$

$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$

$$sin(\theta) = \frac{y}{a}$$

$$\theta = sin^{-1}\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$

$$t_T = \frac{P}{2\pi} \times 2\theta$$

這裡，t_T是發生凌日的週期分數，(2θ/2π)是發生凌日的角度分數。

$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$

通常，a >> R∗ >> Rp。因此，我們可以寫成：

$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$

這裡，P是兩次連續凌日之間的時間間隔。凌日時間與軌道週期相比非常短。因此，

$$t_T = \frac{P}{\pi}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$

這裡，t_T，P，R∗是可觀測量，a和i需要計算得出。

現在，

$$sin(\frac{t_F\pi}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$

其中，y² = (R_∗ − R_p)² − h²。

令，

$$\frac{\Delta F}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$

現在，我們可以表示為：

$$\frac{a}{R_\ast} = \frac{2P}{\pi} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$

對於主序星，

$$R_\ast \propto M^\alpha_\ast$$

$$\frac{R_\ast}{R_0} \propto \left ( \frac{M_\ast}{M_0}\right )^\alpha$$

這給出了R∗。

因此，我們也得到了‘a’的值。

所以，我們得到了'R_p'，'a'和'i'。

對於所有這些，

$$h \leq R_\ast + R_p$$

$$a\: cos\: i \leq R_\ast + R_p$$

即使對於𝑖~89度，凌日持續時間也很短。行星必須非常靠近才能獲得足夠的凌日時間。這給‘i’帶來了嚴格的限制。一旦我們得到‘i’，我們就可以從徑向速度測量中推匯出‘m_p’。

這種透過凌日法進行的探測被稱為機會探測，即觀測到凌日的機率。凌日機率（觀測機率）計算如下所示。

凌日機率與兩個極端凌日構型所描繪的立體角有關，即：

$$行星立體角 = 2\pi \left ( \frac{2R_\ast}{a} \right )$$

以及在半長軸a處的總立體角，或：

$$球體立體角 = 4\pi$$

機率是這兩個面積的比率：

$$= \frac{有利方向所覆蓋的天空面積}{所有可能的軌道方向所覆蓋的天空面積}$$

$= \frac{4\pi a_pR_\ast}{4\pi a^2_p} = \frac{R_\ast}{a_p}$ $\frac{空心圓柱體的面積}{球體的面積}$

這個機率與觀測者無關。

要點

• 凌日法（開普勒太空望遠鏡）用於確定行星的大小。
• 透過凌日法進行的探測是機會探測。
• 行星必須非常靠近才能獲得足夠的凌日時間。
• 凌日機率與行星的立體角有關。
• 此機率與觀測者的參考系無關。