宇宙學 - 徑向速度法

在上一章中，討論了軌道平面和天球平面垂直的圓形軌道情況下的徑向速度法。在這裡，我們處理另一種情況，即圓形軌道的軌道平面和天球平面不垂直。

當軌道平面相對於天球平面成一定角度（不垂直）時，我們有以下情況：

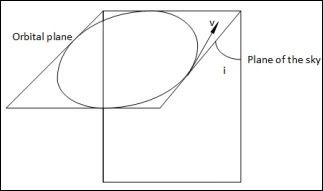
在這種情況下，當它們垂直時，我們有兩個點可以測量真實速度。但在這裡，這是不可能的。在所有點，我們只能測量真實速度v的一個分量。

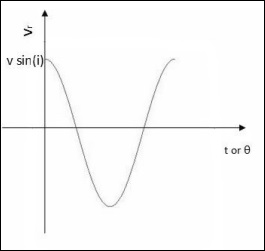
$$v_r = v \:sin(i)cos(\theta)$$

其中θ是軌道的相位，是一個時間相關的量。另一方面，傾角i與時間無關。因此，

$$(v_r)_{max} = v\: sin(i)$$

觀察到的徑向速度曲線將具有以下形式：

當軌道平面垂直於天空時：

$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$

其中m_p, P, G, M∗分別表示行星質量、軌道週期、萬有引力常數和恆星質量。但在這種情況下，我們應該將其修改如下：

$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$

但是，找到i的值是一項困難的任務。我們可以使用凌日法對i的值施加某些約束。行星在恆星和地球之間透過的過程稱為凌日。我們可以透過觀察凌日來獲得光變曲線，光變曲線中觀察到的光通量的顯著下降意味著i接近90度。如果未滿足此類條件，我們無法對i的值有任何瞭解。然後我們找到的m_p值可以作為行星質量的下限，因為它實際上是m_p sin(i)，並且sin(i) ≤ 1。

總之，徑向速度法比凌日法更方便，因為徑向速度可以隨時測量，而凌日測量只能在凌日期間進行，而凌日持續時間可能不長。

要點

• 徑向速度法無法確定行星軌道傾角。

• 徑向速度法優於凌日法，因為徑向速度始終可以測量，而凌日則不然。

• 凌日是短暫的，很容易錯過。