宇宙學 - 輻射主導宇宙

本章將討論與輻射主導宇宙相關的弗裡德曼方程的解。首先，我們將比較物質的能量密度與輻射的能量密度。這將使我們能夠判斷我們的宇宙是物質主導的還是輻射主導的。

輻射的能量密度

目前宇宙中普遍存在的輻射很少能歸因於恆星源，它主要源於殘餘的CMB（宇宙微波背景輻射）。

輻射的能量密度，$\epsilon_{\gamma,0}$，可以表示如下：

$$\epsilon_{\gamma,0} = aT_0^4$$

這裡，a是輻射常數，其表示式為$(8\pi^5k_B^4)/(15h^3c^2)$，等於a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴。我們這裡考慮的溫度T0對應於CMB的相應黑體溫度。

代入結果，我們有：

$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$

在下述計算中，我們假設在一個平坦的宇宙中工作，K = 0。我們將物質的能量密度視為$\epsilon = \rho c^2$。我們考慮以下內容：

$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$

$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$

因此，從上述計算可以看出，我們生活在一個物質主導的宇宙中。這可以從CMB非常冷的事實得到支援。當我們回溯時間時，CMB溫度會升高，我們可以得出結論，可能存在一個宇宙由輻射主導的時期。

流體方程告訴我們：

$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$

如果我們考慮一個塵埃宇宙，則P = 0。撇開之前的結論，我們認為宇宙是由輻射主導的。

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$

利用壓力關係$P_{rad} = \rho c^{2/3}$，我們有：

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$

$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$

進一步簡化，我們有：

$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$

$$\rho_{rad}a^4 =\: constant$$

$$\rho_{rad} \propto \frac{1}{a^4}$$

上述結果表明a與ρ的-4次方反比變化。

這可以從物理上解釋為隨著體積的增加，$a^{-3}$來自於體積變化。剩餘的$a^{-1}$可以被視為光子由於宇宙空間膨脹而損失的能量（宇宙紅移1 + z = a^-1）。

下圖顯示了物質和輻射密度隨時間的變化。

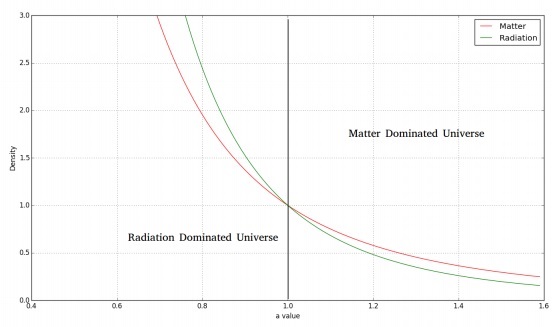
對於一個平坦的輻射主導宇宙，弗裡德曼方程如下：

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$

簡化並應用微分方程的解，我們有：

$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$

$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$

因此，我們有：

$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$

從上述方程可以看出，比例因子的增長率小於塵埃宇宙。

列印頁面