宇宙學 - 羅伯遜-沃克度規

---

---

在本章中，我們將詳細瞭解羅伯遜-沃克度規。

尺度因子隨時間變化的模型

假設一個光子從一個遙遠的星系發射出來。空間在所有方向上對光子都是前進的。宇宙的膨脹是向所有方向進行的。讓我們看看尺度因子在以下步驟中是如何隨時間變化的。

步驟1 - 對於一個靜態宇宙，尺度因子為1，即共動距離的值是物體之間的距離。

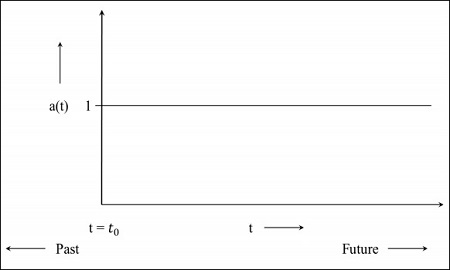
步驟2 - 下圖是宇宙仍在膨脹但膨脹速度正在減小的影像，這意味著該圖將從過去開始。t = 0表示宇宙從該點開始。

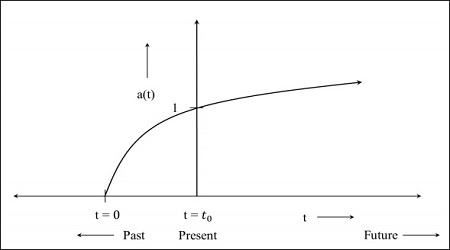
步驟3 - 下圖是宇宙以更快的速度膨脹的影像。

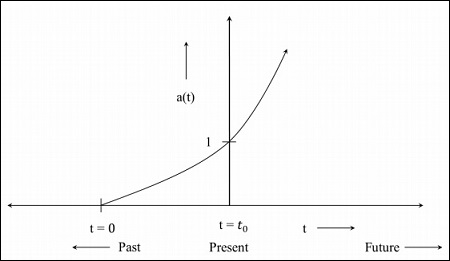
步驟4 - 下圖是宇宙從現在開始收縮的影像。

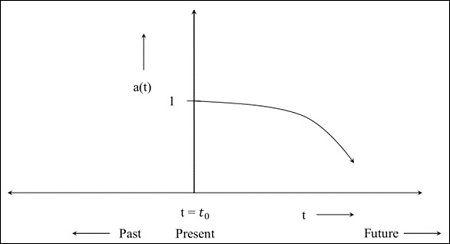
如果尺度因子的值在宇宙收縮過程中變為0，則意味著物體之間的距離變為0，即固有距離變為0。共動距離是現在宇宙中物體之間的距離，是一個常數。在未來，當尺度因子變為0時，所有東西都會靠攏。模型取決於宇宙的成分。

平坦（歐幾里得：沒有曲率引數）膨脹宇宙的度規表示為 -

$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$

對於時空，我們在上述方程中得到的線元被修改為 -

$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$

對於時空，光子發射和探測的時間是不同的。固有距離是物體瞬時的距離，由於宇宙膨脹，它會隨著時間而變化。它是光子從不同的物體傳播到我們這裡所經過的距離。它與共動距離的關係為 -

$$d_p = a(t) \times d_c$$

其中$d_p$是固有距離，$d_c$是共動距離，它是固定的。

在現在宇宙中測量的物體距離被視為共動距離，這意味著共動距離是固定的，不受膨脹的影響。在過去，尺度因子小於1，這表明固有距離更小。

我們可以測量到星系的紅移。因此，固有距離$d_p$對應於$c \times t(z)$，其中$t(z)$是朝向紅移的回溯時間，c是真空中光速。回溯時間是紅移(z)的函式。

基於上述概念，讓我們分析一下宇宙學紅移在這種$d_p = a(t) \times d_c$的場景中是如何解釋的。

假設一個光子（它是地球束縛的）由星系G發射。$t_{em}$對應於光子發射的時間；$a(t_{em})$是光子發射時當時的尺度因子。到光子被探測到時，整個宇宙已經膨脹了，即光子在探測時發生了紅移。$t_{obs}$對應於光子被探測到的時間，相應的尺度因子是$a(t_{obs})$。

宇宙增長了多少倍由以下公式給出 -

$$\frac{a(t_{obs})}{a(t_{em})}$$

波長擴充套件了多少倍為 -

$$\frac{\lambda_{obs}}{\lambda_{em}}$$

這等於宇宙增長了多少倍。符號具有其通常的含義。因此，

$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$

我們知道紅移(z)為 -

$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$

$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$

尺度因子的當前值為1，因此$a(t_{obs}) = 1$，並將過去光子發射時的尺度因子表示為$a(t)$。

因此，

$$1 + z = \frac{1}{a(t)}$$

宇宙學紅移的解釋

為了理解這一點，讓我們舉個例子：如果$z = 2$，那麼$a(t) = 1/3$。

這意味著自光線離開該物體以來，宇宙已經膨脹了三倍。接收到的輻射的波長膨脹了三倍，因為在從發射物體傳播的過程中，空間膨脹了相同的倍數。需要注意的是，在如此大的z值下，紅移主要是宇宙學紅移，它不是物體相對於我們的實際退行速度的有效度量。

對於宇宙微波背景輻射（CMB），z = 1089，這意味著現在的宇宙已經膨脹了∼1090倍。平坦、歐幾里得、膨脹宇宙的度規表示為 -

$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$

我們希望在任何曲率下寫出度規。

羅伯遜和沃克證明了對於任何曲率宇宙（它是均勻且各向同性的），度規表示為 -

$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$

這通常被稱為羅伯遜-沃克度規，對於任何空間拓撲都成立。請注意$dr^2$中的額外因子。這裡𝑘是曲率常數。

宇宙的幾何形狀

宇宙的幾何形狀藉助以下曲率來解釋，包括 -

• 正曲率
• 負曲率
• 零曲率

讓我們詳細瞭解一下這些。

正曲率

如果在曲率表面上的任意一點處畫出的切平面在曲率表面上不與任何點相交，則稱其為具有正曲率的曲面，即曲面位於該點切平面的同一側。球體的表面具有正曲率。

負曲率

如果在曲率表面上的某一點處畫出的切平面與曲率表面上的任意點相交，則稱其為具有負曲率的曲面，即曲面在兩個不同的方向上遠離切平面彎曲。馬鞍形的表面具有負曲率。

現在考慮球體的表面。如果透過連線三個點用測地線（大圓的弧）在球體的表面上構造一個三角形，則球面三角形的內角和大於180^o，即 -

$$\alpha + \beta + \gamma > \pi$$

這樣的空間稱為正曲率空間。此外，曲率是均勻且各向同性的。一般來說，球面三角形頂點的角度遵循以下關係 -

$$\alpha + \beta +\gamma = \pi + A/R^2$$

其中A是三角形的面積，R是球體的半徑。下圖描繪了一個正曲率空間。

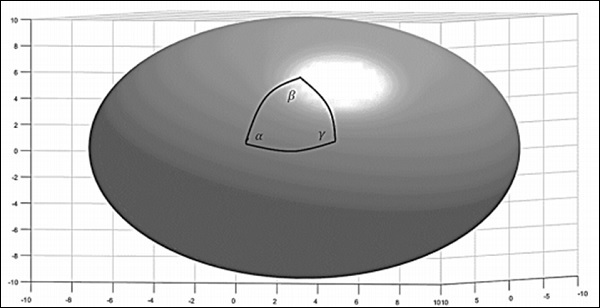
對於正曲率，平行線應該相交。考慮地球的表面，它是一個正曲率空間。在赤道上取兩個起點。垂直穿過赤道的線稱為經線。由於這些線垂直穿過赤道，因此可以將它們稱為平行線。從赤道開始，它們最終會在兩極相交。這種方法被卡爾·弗里德里希·高斯等人用來理解地球的拓撲結構。

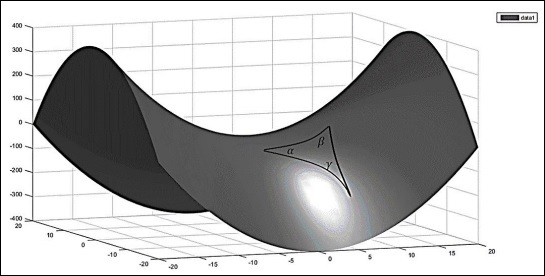
考慮一個負曲率空間（下圖所示的馬鞍），三角形的內角和小於180^o，即 -

$$\alpha + \beta + \gamma < \pi$$

頂點的角度遵循以下關係 -

$$\alpha + \beta + \gamma = \pi - A/R^2$$

零曲率

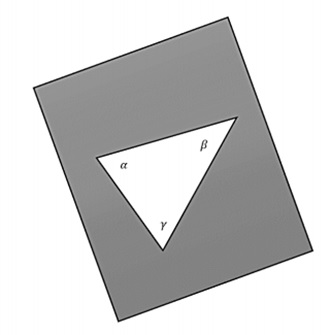
平面表面具有零曲率。現在對於一個平面空間，如果取一個平面，並透過連線三個點用測地線（直線）構造一個三角形，則內角和將為 -

$$\alpha + \beta + \gamma = \pi$$

下圖是一個平坦的二維空間。

如果想要一個空間是均勻且各向同性的，則只有三種可能性：空間可以是均勻平坦的，或者可以具有均勻的正曲率，或者可以具有均勻的負曲率。

曲率常數可以取以下三個值中的任何一個。

$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$

宇宙的全域性拓撲

宇宙具有一定的拓撲結構，但在區域性可能存在皺褶。根據物質在空間中的分佈情況，曲率存在較小的變化。假設存在一類物體，無論其在宇宙中的哪個位置，其真實尺寸都相同，這意味著它們就像標準燭光一樣。它們的亮度不同，但尺寸相同。

如果物體位於正曲率空間中，並且光子來自點A（物體的一端）和點B（物體的另一端），那麼光子將在正曲率空間中沿測地線路徑平行傳播，並最終相遇。對於C處的觀察者來說，它似乎來自不同方向的兩個不同點。

如果物體位於區域性宇宙中，我們測量角尺寸，它不受曲率的影響。如果在更大的紅移處觀察同一類物體，則角尺寸與其不相關。

$$\theta = \frac{d}{r}$$

其中d是物體的尺寸，r是到物體的距離，即如果尺寸大於區域性尺寸，則意味著曲率為正。下圖是正曲率空間中檢測到的光子的示意圖。

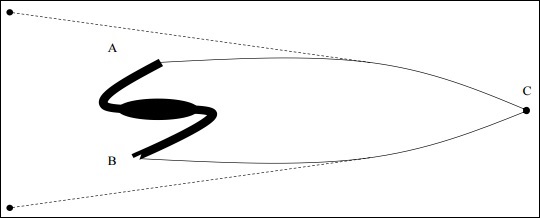
需要注意的是，不存在真正具有標準尺寸和形態的天體物理物體。雖然人們認為巨大的橢圓cD星系符合標準燭光的條件，但後來發現它們也會隨著時間演化。

測量星系距離

在本節中，我們將討論如何透過考慮下圖來測量星系的距離。

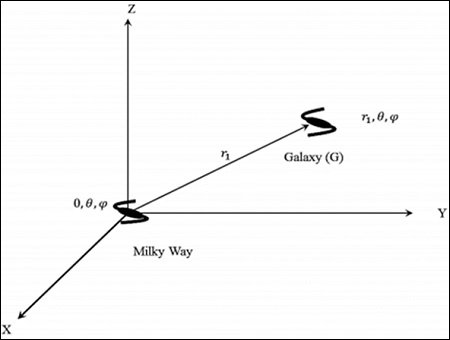
考慮在宇宙靜止參考系中位於(r, θ,)的銀河系。可以透過假設宇宙的均勻性，將𝑟取為0；(0, θ,ϕ)，即宇宙的中心。

考慮位於(r1, θ,)的星系“G”。距離（本徵距離）是光子傳播的最短徑向距離。根據時空的對稱性，從r = 0到r = r1的零測地線在空間中具有恆定的方向。在其徑向傳播過程中，角座標不會改變。如果角座標發生改變，則它不是最短路徑。這就是為什麼dr²中存在曲率項的原因。

要點回顧

• 宇宙的膨脹是向所有方向進行的。

• 宇宙可以是靜態的、膨脹的或收縮的，具體取決於尺度因子的演化。

• cD星系會隨著時間演化，因此不能用作標準燭光。

• 宇宙具有一定的拓撲結構，但在區域性可能存在皺褶。