宇宙學 - 暗能量

暗能量領域在天文學中是一個非常模糊的領域，因為它在所有方程中都是一個自由引數，但我們對其究竟是什麼卻沒有明確的概念。

我們將從弗裡德曼方程開始，

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$

大多數關於宇宙學的入門書籍，它們都從描述哈勃觀測之前，宇宙是封閉且靜態的這一情景開始來介紹暗能量。

現在，為了使宇宙保持靜態，等式右側的兩個項必須相等且都為零。但如果第一項大於第二項，那麼宇宙將不會是靜態的。因此，愛因斯坦將自由引數∧引入場方程以使宇宙保持靜態。他認為，無論第一項與第二項相比如何，只要方程中存在另一個分量，就可以始終得到一個靜態的宇宙，該分量可以補償這兩個項之間的差異。

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$

$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$

其中$P = \rho \ast c^2/3$ 和 $\wedge = \rho \ast c^2$ 是宇宙學常數。（負號僅僅是因為引力是吸引的）

在上式（加速度方程）中 -

第三項起到排斥力的作用，因為方程的另一部分是吸引的。

該方程的物理意義在於˙a = 0，因為當時沒有任何證據表明宇宙正在膨脹。如果這兩個項不匹配，那麼最好新增一個分量，並且根據偏移量，我們始終可以更改自由引數的值。

當時對這個宇宙學常數沒有物理解釋，這就是為什麼當宇宙膨脹的解釋在1920年代被發現時，愛因斯坦立即不得不拋棄這個常數。

這個宇宙學常數的解釋仍在使用，因為它解釋了宇宙的不同版本，但是這個宇宙學常數的定義，其解釋方式隨著時間的推移而不斷變化。

現在，出於許多原因，宇宙學常數的概念已被重新引入宇宙學。其中一個原因是，我們對宇宙不同成分（重子物質、暗物質、輻射）的能量密度進行了觀測，因此我們知道這個引數是什麼。使用宇宙微波背景輻射進行的獨立觀測表明k=0。

$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: 氫原子.m^{-3}$$

為了使k為0，ρ必須等於ρc，但如果我們把我們知道的所有東西加起來，它並不等於0，這意味著存在某個其他分量，表明它遠小於ρc。

$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$

暗能量的另一個證據來自Ia型超新星觀測，當白矮星吸積物質並超過錢德拉塞卡極限時發生Ia型超新星爆發，這是一個非常精確的極限（≈ 1.4M）。現在，每次發生Ia型超新星爆發時，我們都具有相同的質量，這意味著系統的總結合能相同，並且我們所能看到的光能也相同。

當然，超新星的光會先增強然後減弱，但是如果你測量峰值亮度，它總是相同的，這使其成為一個標準的觀測物件。因此，藉助Ia型超新星，我們用來測量宇宙的宇宙學成分，天文學家發現，高紅移的超新星比低紅移的超新星暗30％-40％，如果存在任何非零∧項，則可以解釋這一點。

在宇宙學模型中，DE（暗能量）被視為一種流體，這意味著我們可以寫出它的狀態方程。狀態方程是連線物質兩種不同狀態的變數（如壓強、密度、溫度和體積）的方程。

從量綱上看，

$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$

$$\rho_\wedge = \frac{\wedge}{8\pi G}$$

DE的能量密度，

$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$

暗能量密度引數，

$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$

Ω∧是暗能量密度相對於臨界密度的值。

$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$

關於暗能量，有很多理論，它正在排斥宇宙並導致宇宙膨脹。一個假設是，這種暗能量可能是真空能量密度。假設空間本身正在處理一些能量，當你在空間的單位體積內計算重子物質、暗物質和輻射的量時，你也在計算與空間相關的能量的量，但尚不清楚暗能量是否真的是真空能量密度。

我們知道暗物質和輻射的密度與尺度因子之間的關係是，

$$\rho_m \propto \frac{1}{a^3}$$

$$\rho_m \propto \frac{1}{a^4}$$

我們繪製了密度與尺度因子的關係圖。在同一張圖中，我們可以看到ρ∧隨著宇宙的膨脹保持不變，它不依賴於尺度因子。

下圖顯示了密度與尺度因子之間的關係。

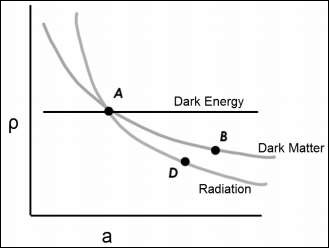
‘ρ’與‘a’（尺度因子與時間相關）在同一張圖中，暗能量被建模為一個常數。因此，無論我們在當前宇宙中測量到多少暗能量，它都是一個常數。

要點

列印頁面