哈勃引數與比例因子

本章將討論哈勃引數和比例因子。

哈勃常數與比例因子的分數變化率

在本節中，我們將哈勃常數與比例因子的分數變化率聯絡起來。

我們可以用以下方式寫出速度並簡化。

$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$

$$= \frac{d[a(t)r_c]}{dt}$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$

這裡，v是退行速度，a是比例因子，r_p是星系間的固有距離。

哈勃經驗公式的形式為：

$$v = H \ast r_p$$

因此，比較上述兩個方程，我們得到：

哈勃引數 = 比例因子的分數變化率

$$H = \frac{da}{dt} \ast \frac{1}{a}$$

注意 - 這不是一個常數，因為比例因子是時間的函式。因此它被稱為哈勃引數而不是哈勃常數。

經驗上我們寫成：

$$H = \frac{V}{D}$$

因此，從這個方程中，我們可以推斷，由於D在增加而V是一個常數，那麼H隨著時間的推移和宇宙的膨脹而減小。

在本節中，我們將瞭解如何結合羅伯遜-沃克模型使用弗裡德曼方程。為了理解這一點，讓我們以以下影像為例，該影像中有一個距離為r_p的測試質量，距離質量為M的天體。

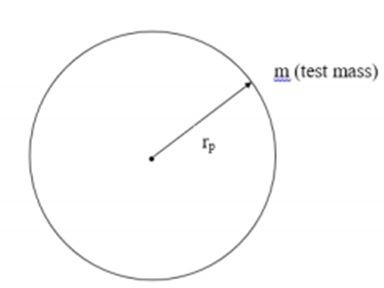
考慮到上圖，我們可以將力表示為：

$$F = G \ast M \ast \frac{m}{r^2_p}$$

這裡，G是萬有引力常數，ρ是可觀測宇宙內的物質密度。

現在，假設球體內質量密度均勻，我們可以寫成：

$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$

將這些代入我們的力方程，我們得到：

$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$

因此，我們可以將質量m的勢能和動能寫成：

$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$

$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$

使用維裡定理：

$$U = K.E + V$$

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

但是這裡，$r_p = ar_c$。所以我們得到：

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

進一步簡化後，我們得到弗裡德曼方程：

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$

這裡U是一個常數。我們還注意到，我們目前生活的宇宙是由物質主導的，而輻射能量密度非常低。

列印頁面