宇宙學度規與膨脹

根據能量守恆定律和質量守恆定律，包括質量在內的總能量 (E=mc²) 在宇宙中任何過程的每一步都保持不變。宇宙的膨脹本身會消耗能量，這可能來自光子波長的拉伸（宇宙紅移）、暗能量相互作用等。

為了加快對超過26,000個星系的調查，Stephen A. Shectman設計了一種能夠同時測量112個星系的儀器。在一個金屬板上，鑽出了與天空星系位置對應的孔。光纖電纜將每個星系的光傳輸到位於智利拉斯坎帕納斯天文臺2.5米杜邦望遠鏡上的光譜儀上的獨立通道。

為了達到最大效率，使用了被稱為漂移掃描測光法的專業技術，其中望遠鏡指向調查區域的起點，然後關閉自動驅動。望遠鏡靜止不動，天空漂移而過。計算機以與地球自轉相同的速率讀取CCD探測器的資訊，產生一個在恆定天球緯度上長時間連續的影像。測光總共花費了450小時。

存在不同形式的噪聲，其數學建模取決於其特性而不同。各種物理過程在大尺度上演化了宇宙的功率譜。由於量子漲落而賦予的初始功率譜遵循頻率的負三次冪，這是一種三維的粉紅噪聲譜。

度規

在宇宙學中，首先必須對空間有一個定義。度規是描述空間中點的數學表示式。對天空的觀測是在球面幾何中進行的；因此，將使用球座標系。兩個緊密間隔的點之間的距離由下式給出：

$$ds^2 = dr^2 + r^2\theta ^2 + r^2 sin^2\theta d\phi^2$$

下圖顯示了三維非膨脹歐幾里得空間中的幾何形狀。

該幾何形狀仍然在三維非膨脹歐幾里得空間中。因此，定義框架本身的參考網格將是膨脹的。下圖描述了增強的度規。

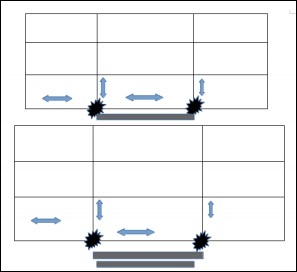
將比例因子放入非膨脹空間的方程中，稱為“比例因子”，它結合了宇宙相對於時間的膨脹。

$$ds^2 = a^2(t)\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$

其中a(t)是比例因子，有時寫成R(t)。而a(t) > 1表示度規的放大，a(t) < 1表示度規的縮小，a(t) = 1表示度規恆定。按照慣例，a(t₀) = 1。

在共同移動座標系中，測量尺度與框架（膨脹宇宙）一起膨脹。

這裡，$\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$是共同移動距離，$ds^2$是固有距離。

固有距離將對應於在觀測時刻測量的從地球到遙遠星系的實際距離，即物體的瞬時距離。

這是因為光子從遙遠光源到達觀察者時所走的距離將在觀察者的$t=t_0$時刻接收，這意味著觀察到的瞬時距離將是固有距離，並且可以使用速率因子和初始測量長度作為參考來預測未來的距離。

共同移動距離和固有距離的概念對於測量觀測空間給定體積中星系實際數量密度值非常重要。必須使用共同移動距離來計算觀測光子發射時星系的密度。一旦可以估計宇宙的膨脹速率，就可以獲得該密度。

為了估計膨脹速率，可以觀察長時間內觀測到的遙遠星系的距離變化。

列印頁面