紅移和後退速度

---

---

哈勃的觀測利用了徑向速度與譜線位移相關的事實。在這裡，我們將觀察四種情況，並找到後退速度（$v_r$）和紅移 (z) 之間的關係。

情況一：源運動的非相對論性情況

在這種情況下，v遠小於c。光源發出某種訊號（聲音、光等），該訊號以波陣面的形式傳播。在源參考系中，兩個連續訊號傳送之間的時間間隔為Δts。在觀察者參考系中，兩個連續訊號接收之間的時間間隔為Δto。

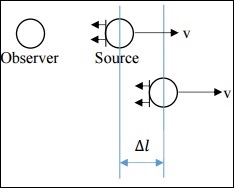
如果觀察者和光源都是靜止的，則Δts = Δto，但這裡並非如此。相反，關係如下。

$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$

現在，$\Delta l = v \Delta t_s$

此外，由於（波速×時間）=波長，我們得到

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$

根據上述方程式，我們得到以下關係：

$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$

其中$\lambda _s$是光源處訊號的波長，$\lambda _o$是觀察者解釋的訊號波長。

在這裡，由於光源正在遠離觀察者，因此v為正。

紅移：

$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$

根據上述方程式，我們得到紅移如下。

$$z = \frac{v}{c}$$

情況二：觀察者運動的非相對論性情況

在這種情況下，v遠小於c。這裡，Δl不同。

$$\Delta l = v \Delta t_o$$

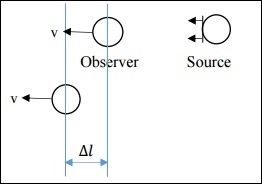
簡化後，我們得到：

$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$

我們得到紅移如下：

$$z = \frac{v/c}{1-v/c}$$

由於v << c，情況一和情況二的紅移表示式近似相同。

讓我們看看上面兩種情況下獲得的紅移有何不同。

$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$

因此，由於$(v/c)^2$因子，$z_{II} − z_{I}$是一個非常小的數字。

這意味著，如果v << c，我們無法判斷光源是運動的還是靜止的。

現在讓我們瞭解狹義相對論基礎(Special Theory of Relativity)：

• 光速是一個常數。

• 當光源（或觀察者）以與光速相當的速度運動時，會觀察到相對論效應。

• 時間膨脹：$\Delta t_o = \gamma \Delta t_s$

• 長度收縮：$\Delta l_o = \Delta t_s/\gamma$

• 這裡，$\gamma$是洛倫茲因子，大於1。

$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$

情況三：光源運動的相對論性情況

在這種情況下，v與c相當。參考與情況一相同的圖形。由於相對論效應，觀察到時間膨脹，因此獲得以下關係。（光源以相對論速度運動）

$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$

$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$

進一步簡化後，我們得到：

$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$

上述表示式稱為運動多普勒頻移表示式。

情況四：觀察者運動的相對論性情況

參考與情況二相同的圖形。由於相對論效應，觀察到時間縮短，因此獲得以下關係。（觀察者以相對論速度運動）

$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$

$$\Delta l = \frac{v\Delta t_o}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$

進一步簡化後，我們得到：

$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$

上述表示式與我們在情況三中得到的結果相同。

要點

• 恆星的後退速度和紅移是相關的量。

• 在非相對論性情況下，我們無法確定光源是運動的還是靜止的。

• 在相對論性情況下，光源或觀察者運動的紅移-後退速度關係沒有區別。

• 運動的鐘走得慢，是相對論的直接結果。