
- 宇宙學教程
- 宇宙學 - 首頁
- 膨脹宇宙
- 造父變星
- 紅移和退行速度
- 紅移與運動學多普勒頻移
- 宇宙度規與膨脹
- 羅伯遜-沃爾克度規
- 哈勃引數與比例因子
- 弗裡德曼方程與宇宙模型
- 流體方程
- 物質主導宇宙
- 輻射主導宇宙
- 暗能量
- 螺旋星系旋轉曲線
- 星系速度彌散測量
- 哈勃引數與密度引數
- 宇宙年齡
- 角直徑距離
- 光度距離
- Ia型超新星
- 宇宙微波背景輻射
- CMB - 解耦時的溫度
- CMB輻射的各向異性與COBE衛星
- CMB各向異性的模型
- 最後散射面上的視界長度
- 太陽系外行星探測
- 徑向速度法
- 凌日法
- 系外行星特性
- 宇宙學有用資源
- 宇宙學速成指南
- 宇宙學 - 有用資源
- 宇宙學 - 討論
宇宙學速成指南
宇宙學 - 膨脹宇宙
宇宙學是研究宇宙的學科。追溯到過去,關於宇宙起源存在著幾種不同的學派。許多學者相信穩態理論。根據這一理論,宇宙始終保持不變,它沒有開端。
而另一部分人則相信大爆炸理論。這一理論預測了宇宙的開端。有證據表明大爆炸留下了熱的殘餘輻射,這再次支援了該模型。大爆炸理論預測了宇宙中輕元素的丰度。因此,遵循著名的大爆炸模型,我們可以說宇宙有一個開端。我們生活在一個膨脹的宇宙中。
哈勃紅移
在20世紀初,最先進的望遠鏡,威爾遜山天文臺的100英寸望遠鏡,是當時最大的望遠鏡。哈勃是使用該望遠鏡工作的傑出科學家之一。他發現銀河系外還有星系。河外天文學只有100年的歷史。威爾遜山天文臺是最大的望遠鏡,直到帕洛馬山天文臺建成,擁有200英寸的望遠鏡。
哈勃並不是唯一一個觀測到銀河系外星系的科學家,休馬森幫助了他。他們開始測量附近星系的頻譜。然後他們觀察到星系光譜在可見波長範圍內有連續發射。在連續譜的頂部有發射線和吸收線。從這些譜線,我們可以估計星系是遠離我們還是靠近我們。
當我們得到一個光譜時,我們假設最強烈的譜線來自H-α。根據文獻,最強烈的譜線應該出現在6563 Å,但如果譜線出現在7000Å附近,我們可以很容易地說它是紅移的。
根據狹義相對論,
$$1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$$
其中,Z是紅移,一個無量綱數,v是退行速度。
$$\frac{\lambda_{obs}}{\lambda_{rest}} = 1 + z$$
哈勃和休馬森在他們的論文中列出了22個星系。幾乎所有這些星系都表現出紅移。他們繪製了速度(km/s)與距離(Mpc)的關係圖。他們觀察到了一種線性趨勢,哈勃提出了他著名的定律如下。
$$v_r = H_o d$$
這是哈勃紅移距離關係。下標r表示膨脹是徑向的。其中,$v_r$是退行速度,$H_o$是哈勃引數,d是星系到我們的距離。他們得出結論:如果宇宙的膨脹速度是均勻的,那麼遠離我們的星系退行速度越快。
膨脹
一切都在遠離我們。星系不是靜止的,總有一些膨脹的諧波。哈勃引數的單位是km sec−1Mpc−1。如果距離為-1 Mpc,星系將以200 kms/sec的速度移動。哈勃引數給了我們膨脹的速度。根據哈勃和休馬森的研究,$H_o$的值為200 kms/sec/Mpc。
資料顯示所有星系都在遠離我們。因此,很明顯我們位於宇宙的中心。但哈勃並沒有犯這個錯誤,在他看來,無論我們生活在哪個星系,我們都會發現所有其他星系都在遠離我們。因此,結論是星系之間的空間膨脹,宇宙沒有中心。
膨脹發生在任何地方。然而,有一些力正在對抗膨脹。化學鍵、萬有引力和其他的吸引力將物體結合在一起。早期所有物體都靠得很近。考慮到大爆炸是一種衝量力,這些物體開始彼此遠離。
時間尺度
在區域性尺度上,動力學受引力支配。在最初的哈勃定律中,有一些星系顯示出藍移。這可以歸因於星系的組合引力勢。引力使一些事物脫離了哈勃定律。仙女座星系正在向我們靠近。引力試圖減慢速度。最初膨脹正在減慢,現在正在加速。
由於這個原因,出現了一個宇宙急轉彎。對哈勃引數進行了幾次估計。在90年中,它從500 kms/sec/Mpc發展到69 kms/sec/Mpc。值的差異是由於距離的低估。造父變星被用作距離校準器,但是有不同型別的造父變星,在估計哈勃引數時沒有考慮這一事實。
哈勃時間
哈勃常數給了我們對宇宙年齡的現實估計。如果星系一直以相同的速度運動,則$H_o$將給出宇宙的年齡。$H_o$的倒數給了我們哈勃時間。
$$t_H = \frac{1}{H_o}$$
用$H_o$的當前值替換,$t_H$ = 140億年。從宇宙開始以來,膨脹速度一直保持不變。即使事實並非如此,$H_o$也為宇宙的年齡提供了一個有用的上限。假設膨脹速度恆定,當我們繪製距離和時間之間的關係圖時,圖的斜率由速度給出。
在這種情況下,哈勃時間等於實際時間。然而,如果宇宙過去膨脹得更快,現在膨脹得更慢,那麼哈勃時間給出了宇宙年齡的上限。如果宇宙以前膨脹得較慢,現在正在加速,那麼哈勃時間將給出宇宙年齡的下限。
$t_H = t_{age}$ − 如果膨脹速度恆定。
$t_H > t_{age}$ − 如果宇宙過去膨脹得更快,現在膨脹得更慢。
$t_H < t_{age}$ − 如果宇宙過去膨脹得更慢,現在膨脹得更快。
考慮一組10個星系,它們與另一組星系的距離為200 Mpc。星系團內的星系永遠不會認為宇宙正在膨脹,因為區域性星系團內的動力學受引力支配。
要點
宇宙學是研究我們宇宙過去、現在和未來的學科。
我們的宇宙大約有140億年的歷史。
宇宙正在不斷膨脹。
哈勃引數是衡量宇宙年齡的指標。
Ho的當前值為69 kms/sec/Mpc。
宇宙學 - 造父變星
很長一段時間內,沒有人認為銀河系外存在星系。1924年,埃德溫·哈勃在仙女座星雲中探測到造父變星並估計了它們的距離。他得出結論,這些“螺旋星雲”實際上是其他星系,而不是我們銀河系的一部分。因此,他確定M31(仙女座星系)是一個島宇宙。這是河外天文學的誕生。
造父變星表現出週期性的亮度下降。觀測表明,連續下降之間的時間間隔(稱為脈動週期)與光度有關。因此,它們可以用作距離指示器。像太陽這樣的主序星處於流體靜力平衡狀態,它們在其核心燃燒氫。氫完全燃燒後,恆星向紅巨星階段移動,並試圖恢復其平衡。
造父變星是主序星之後,正在從主序星向紅巨星過渡的恆星。
造父變星的分類
這些脈動變星主要分為3類:
I型造父變星(或經典造父變星)− 週期為30-100天。
II型造父變星(或室女座W型星)− 週期為1-50天。
天琴座RR型變星 − 週期為0.1-1天。
當時,哈勃不知道這種變星的分類。這就是為什麼哈勃常數被高估的原因,因此他估計了我們宇宙的較低年齡。因此,退行速度也被高估了。在造父變星中,擾動從恆星中心徑向向外傳播,直到達到新的平衡。
亮度和脈動週期之間的關係
現在讓我們嘗試理解這樣一個事實的物理基礎:更高的脈動週期意味著更高的亮度。考慮一顆光度為L,質量為M的恆星。
我們知道:
$$L \propto M^\alpha$$
其中,對於低質量恆星,α = 3到4。
根據斯特藩-玻爾茲曼定律,我們知道:
$$L \propto R^2 T^4$$
如果R是半徑,$c_s$是聲速,那麼脈動週期P可以寫成:
$$P = R/c_s$$
但是,任何介質中的聲速都可以用溫度表示為:
$$c_s = \sqrt{\frac{\gamma P}{\rho}}$$
這裡,對於等溫情況,γ 為 1。
對於理想氣體,P = nkT,其中 k 為玻爾茲曼常數。因此,我們可以寫成:
$$P = \frac{\rho kT}{m}$$
其中 ρ 為密度,m 為質子的質量。
因此,週期由下式給出:
$$P \cong \frac{Rm^{\frac{1}{2}}}{(kT)^{{\frac{1}{2}}}}$$
維裡定理指出,對於穩定、自引力、球形分佈的等質量物體(如恆星、星系),物體的總動能k等於總引力勢能u的負二分之一,即:
$$u = -2k$$
讓我們假設維裡定理對這些變星成立。如果我們考慮一顆恆星表面上的質子,那麼根據維裡定理,我們可以說:
$$\frac{GMm}{R} = mv^2$$
根據麥克斯韋分佈:
$$v = \sqrt{\frac{3kT}{2}}$$
因此,週期:
$$P \sim \frac{RR^{\frac{1}{2}}}{(GM)^{\frac{1}{2}}}$$
這意味著
$$P \propto \frac{R^{\frac{3}{2}}}{M^{\frac{1}{2}}}$$
我們知道 – $M \propto L^{1/\alpha}$
還有 $R \propto L^{1/2}$
因此,對於β > 0,我們最終得到 – $P \propto L^\beta$
要點
造父變星是主序後恆星,它們正在從主序星轉變為紅巨星。
造父變星分為三種類型:I 型、II 型和 RR Lyrae 型,其脈動週期依次遞減。
造父變星的脈動週期與其亮度(光度)成正比。
紅移和退行速度
哈勃的觀測利用了徑向速度與譜線位移相關的這一事實。在這裡,我們將觀察四種情況,並找到退行速度($v_r$)和紅移 (z) 之間的關係。
情況 1:運動源的非相對論性情況
在這種情況下,v遠小於c。光源正在發射某種訊號(聲音、光等),該訊號以波陣面的形式傳播。在源參考系中,連續兩個訊號之間的時間間隔為Δts。在觀察者參考系中,連續兩個訊號之間的時間間隔為Δto。
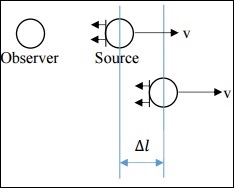
如果觀察者和光源都是靜止的,那麼 Δts = Δto,但這裡並非如此。相反,關係如下。
$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$
現在,$\Delta l = v \Delta t_s$
此外,由於(波速 × 時間)= 波長,我們得到
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$
根據以上等式,我們得到以下關係:
$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$
其中 $\lambda _s$ 是光源處訊號的波長,$\lambda _o$ 是觀察者解釋的訊號的波長。
在這裡,由於光源正在遠離觀察者,因此v為正。
紅移:
$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$
根據以上等式,我們得到如下紅移:
$$z = \frac{v}{c}$$
情況 2:運動觀察者的非相對論性情況
在這種情況下,v遠小於c。這裡,$\Delta l$不同。
$$\Delta l = v \Delta t_o$$
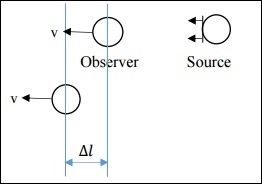
簡化後,我們得到:
$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$
我們得到如下紅移:
$$z = \frac{v/c}{1-v/c}$$
由於v << c,情況 I 和情況 II 的紅移表示式近似相同。
讓我們看看上面兩種情況下獲得的紅移有何不同。
$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$
因此,由於 $(v/c)^2$ 項,$z_{II} − z_{I}$ 是一個非常小的數。
這意味著,如果 v << c,我們無法判斷是光源在運動,還是觀察者在運動。
現在讓我們瞭解狹義相對論 (STR) 的基礎:
光速是一個常數。
當光源(或觀察者)以與光速相當的速度運動時,就會觀察到相對論效應。
時間膨脹:$\Delta t_o = \gamma \Delta t_s$
長度收縮:$\Delta l_o = \Delta t_s/\gamma$
這裡,γ 是洛倫茲因子,大於 1。
$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$
情況 3:運動光源的相對論性情況
在這種情況下,v與c相當。參考與情況 I 相同的圖。由於相對論效應,觀察到時間膨脹,因此得到以下關係。(光源以相對論速度運動)
$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$
$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$
進一步簡化後,我們得到:
$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$
上述表示式稱為運動學多普勒頻移表示式。
情況 4:運動觀察者的相對論性情況
參考與情況 II 相同的圖。由於相對論效應,觀察到時間縮短,因此得到以下關係。(觀察者以相對論速度運動)
$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$
$$\Delta l = \frac{v\Delta t_o}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$
進一步簡化後,我們得到:
$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$
上述表示式與情況 III 得到的結果相同。
要點
恆星的退行速度和紅移是相關的量。
在非相對論性情況下,我們無法確定光源是運動的還是靜止的。
在相對論性情況下,對於運動的光源或觀察者,紅移與退行速度的關係沒有區別。
運動的時鐘走得慢,是相對論的直接結果。
紅移與運動學多普勒頻移
紅移z = 10的星系對應於v≈80%的c。如果考慮暗物質,銀河系的質量約為1011M⊙,則為1012M⊙。因此,我們的銀河系非常巨大。如果它以 80% 的c運動,則不符合物體如何運動的普遍概念。
我們知道:
$$\frac{v_r}{c} = \frac{\lambda_{obs} - \lambda{rest}}{\lambda_{rest}}$$
對於z的小值:
$$z = \frac{v_r}{c} = \frac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}}$$
在下圖中,通量和波長之間的關係圖中,在連續譜的頂部有發射線。根據H-α線資訊,我們可以得出結論,大約z = 7。這意味著星系以 70% 的c運動。我們正在觀察位移並將其解釋為速度。我們應該擺脫這種概念,並以不同的方式看待z。想象一下空間是一個二維網格,它代表了宇宙,如下所示。

將黑星視為我們自己的銀河系,將藍星視為另一個星系。當我們記錄來自這個星系的光時,我們看到光譜並找出它的紅移,即星系正在遠離。當光子發射時,它具有相對速度。
如果空間正在膨脹會怎樣?
這是光子的瞬時紅移。兩個星系之間空間的累積紅移將趨於大的紅移。波長最終會改變。這是空間的膨脹,而不是星系的運動學運動。
下圖顯示,如果相互引力超過膨脹,那麼它就不參與哈勃定律。

在運動學多普勒頻移中,紅移是在發射時誘導到光子中的。在宇宙紅移中,每一步都會累積紅移。在引力勢中,光子將發生藍移。當它從引力勢中爬出來時,它會發生紅移。
根據狹義相對論,兩個彼此經過的物體之間的相對速度不能大於光速。我們所說的速度是宇宙膨脹的速度。對於較大的 z 值,紅移是宇宙的,而不是相對於我們而言物體實際退行速度的有效測量。
宇宙原理
它源於宇宙的哥白尼學說。根據這個學說,宇宙是均勻且各向同性的。宇宙中沒有首選方向和位置。
均勻性意味著無論你居住在宇宙的哪個部分,你都會看到宇宙在各個部分都是相同的。各向同性意味著無論你朝哪個方向看,你都會看到相同的結構。
均勻性的一個合適的例子是稻田。從各個部分看它都是均勻的,但是當風吹過時,它的方向會有變化,因此它不是各向同性的。考慮一塊平地上的山,一個觀察者站在山頂上。他會看到平地的各向同性,但它不是均勻的。如果在一個均勻的宇宙中,在一個點上是各向同性的,那麼它在任何地方都是各向同性的。
已經進行了大規模的調查以繪製宇宙圖。斯隆數字巡天就是這樣一項調查,它不太關注赤緯,而關注赤經。回溯時間約為 20 億年。每個畫素對應於星系的位置,顏色對應於形態結構。綠色代表藍色螺旋星系,而紅色偽彩色表示大質量星系。
星系存在於宇宙網的細絲狀結構中,星系之間存在空洞。
$\delta M/M \cong 1$,即質量分佈的波動為 1,M 是給定立方體中存在的物質質量。在這種情況下,取體積為 50 Mpc 的立方體。
對於邊長為 1000 Mpc 的立方體,$\delta M/M \cong 10^{−4}$。
量化均勻性的一種方法是取質量波動。在較小的尺度上,質量波動會更高。
為了量化各向同性,考慮宇宙微波背景輻射。宇宙在大角度尺度上幾乎是各向同性的。
要點
兩個彼此經過的物體之間的相對速度不能大於光速。
宇宙原理指出宇宙是均勻且各向同性的。
這種均勻性存在於非常大的角度尺度上,而不是較小的尺度上。
SDSS(斯隆數字巡天)是繪製夜空圖的努力,驗證了宇宙原理。
宇宙度規與膨脹
根據能量守恆定律和質量守恆定律,包括質量在內的總能量 (E=mc2) 在宇宙中任何過程的每一步都保持不變。宇宙的膨脹本身消耗能量,這可能是來自光子波長(宇宙紅移)的拉伸、暗能量相互作用等等。
為了加快對超過26,000個星系的巡天速度,史蒂芬·A·謝克特曼(Stephen A. Shectman)設計了一種能夠同時測量112個星系的儀器。在一個金屬板上鑽孔,這些孔對應於天空中星系的位置。光纖電纜將來自每個星系的光傳輸到智利拉斯坎帕納斯山卡內基天文臺(Carnegie Observatories)的2.5米杜邦望遠鏡上的光譜儀的獨立通道。
為了達到最大效率,使用了被稱為漂移掃描測光法(Drift-Scan Photometry)的專業技術,其中望遠鏡指向觀測區域的起始點,然後關閉自動驅動。望遠鏡靜止不動,天空則漂移過去。計算機以與地球自轉相同的速率讀取來自CCD探測器(CCD Detector)的資訊,從而產生一個在恆定天球緯度上的長而連續的影像。測光工作總共花費了450小時。
存在不同形式的噪聲,其數學模型取決於其特性。各種物理過程在大尺度上改變了宇宙的功率譜。由於量子漲落賦予的初始功率譜遵循頻率的負三次方,這是一種三維的粉紅噪聲譜(Pink Noise Spectrum)。
度量
在宇宙學中,首先必須對空間進行定義。度量是描述空間中點的數學表示式。天空的觀測是在球面幾何中進行的;因此,將使用球座標系。兩個緊密間隔的點之間的距離由下式給出:
$$ds^2 = dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2$$
下圖顯示了三維非膨脹歐幾里得空間中的幾何形狀。

此幾何形狀仍然位於三維非膨脹歐幾里得空間中。因此,定義框架本身的參考網格將是膨脹的。下圖描繪了增大的度量。
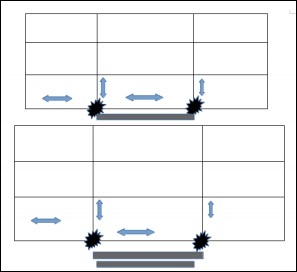
將一個比例因子放入非膨脹空間的方程中,稱為“比例因子”,它包含了宇宙相對於時間的膨脹。
$$ds^2 = a^2(t)\left [ dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$
其中a(t)是比例因子,有時寫成R(t)。而a(t) > 1表示度量的放大,a(t) < 1表示度量的縮小,a(t) = 1表示度量恆定。按照慣例,a(t0) = 1。
共動座標系
在共動座標系(Comoving Coordinate System)中,測量尺度與框架(膨脹宇宙)一起膨脹。
這裡,$\left [ dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$是共動距離,$ds^2$是固有距離。
固有距離將對應於在觀測時刻測量的遙遠星系到地球的實際距離,也就是物體的瞬時距離。
這是因為光子從遙遠光源到達觀測者時所經過的距離是在觀測者的$t=t_0$時刻接收到的,這意味著瞬時觀測距離將是固有距離,並且可以使用速率因子和初始測量長度作為參考來預測未來的距離。
共動距離和固有距離的概念對於測量觀測空間給定體積內星系實際數密度值非常重要。必須使用共動距離來計算觀測到的光子發射時星系的密度。一旦可以估計宇宙的膨脹速率,就可以獲得這個值。
為了估計膨脹速率,可以觀測長時間內觀測到的遙遠星系的距離變化。
要點
度量是描述空間中點的數學表示式。
比例因子決定宇宙是收縮還是膨脹。
在共動座標系中,測量尺度與框架(膨脹宇宙)一起膨脹。
固有距離是物體的瞬時距離。
共動距離是物體的實際距離。
宇宙學 - 羅伯遜-沃克度量
在本章中,我們將詳細瞭解羅伯遜-沃克度量。
隨時間變化的比例因子的模型
假設一個光子從遙遠的星系發出。空間對於光子來說在各個方向上都是向前的。宇宙的膨脹是在所有方向上進行的。讓我們看看比例因子如何在以下步驟中隨時間變化。
步驟1 - 對於靜態宇宙,比例因子為1,即共動距離的值是物體之間的距離。
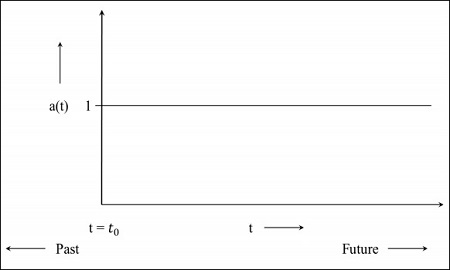
步驟2 - 下圖是宇宙仍在膨脹但以減速率膨脹的圖,這意味著該圖將從過去開始。t = 0表示宇宙從那時開始。
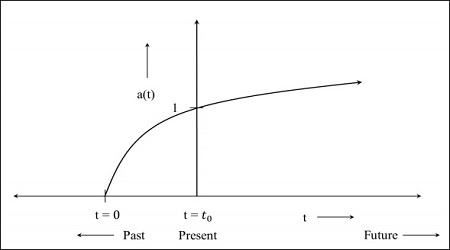
步驟3 - 下圖是宇宙以更快速度膨脹的圖。
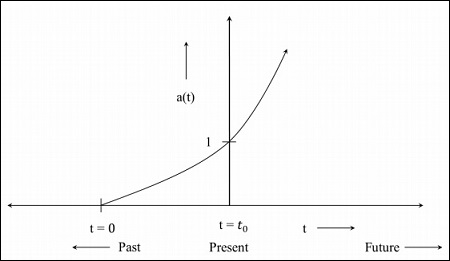
步驟4 - 下圖是從現在開始收縮的宇宙圖。
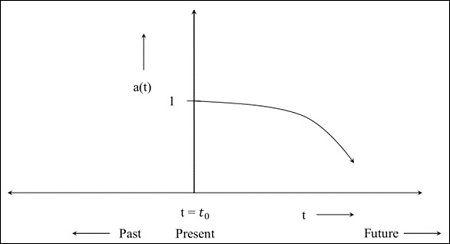
如果在宇宙收縮過程中比例因子的值變為0,則意味著物體之間的距離變為0,即固有距離變為0。共動距離是當前宇宙中物體之間的距離,是一個常數。未來,當比例因子變為0時,所有東西都會靠攏。該模型取決於宇宙的組成部分。
平坦(歐幾里得:沒有曲率引數)膨脹宇宙的度量表示為:
$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$
對於時空,我們在上式中得到的線元素修改為:
$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$
對於時空,光子發射和探測的時間是不同的。固有距離是物體的瞬時距離,由於宇宙的膨脹,它會隨著時間而變化。它是光子從不同的物體傳播到我們這裡所經過的距離。它與共動距離的關係如下:
$$d_p = a(t) \times d_c$$
其中$d_p$是固有距離,$d_c$是共動距離,它是固定的。
在當前宇宙中測量的到物體的距離被認為是共動距離,這意味著共動距離是固定的,不會因膨脹而改變。在過去,比例因子小於1,這表明固有距離較小。
我們可以測量到星系的紅移。因此,固有距離$d_p$對應於$c \times t(z)$,其中$t(z)$是朝向紅移的回溯時間,c是真空中的光速。回溯時間是紅移(z)的函式。
基於上述概念,讓我們分析在這種$d_p = a(t) \times d_c$的情況下如何解釋宇宙紅移。
假設一個光子(地球上的)由星系G發射。$t_{em}$對應於光子發射的時間;$a(t_{em})$是光子發射時當時的比例因子。到光子被探測到時,整個宇宙已經膨脹了,即光子在探測時發生了紅移。$t_{obs}$對應於光子被探測到的時間,相應的比例因子為$a(t_{obs})$。
宇宙增長因子由下式給出:
$$\frac{a(t_{obs})}{a(t_{em})}$$
波長膨脹因子為:
$$\frac{\lambda_{obs}}{\lambda_{em}}$$
它等於宇宙增長因子。符號具有其通常的含義。因此,
$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$
我們知道紅移(z)為:
$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$
$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$
比例因子的當前值為1,因此$a(t_{obs}) = 1$,並將光子過去發射時的比例因子表示為$a(t)$。
因此,
$$1 + z = \frac{1}{a(t)}$$
宇宙學中紅移的解釋
為了理解這一點,讓我們舉個例子:如果$z = 2$,則$a(t) = 1/3$。
這意味著自從光離開那個物體以來,宇宙已經膨脹了三倍。接收到的輻射的波長膨脹了三倍,因為在其從發射物體傳播的過程中,空間膨脹了相同的倍數。應該注意的是,對於如此大的z值,紅移主要是宇宙紅移,它不是物體相對於我們的實際退行速度的有效度量。
對於宇宙微波背景輻射(CMB),z = 1089,這意味著當前宇宙已經膨脹了∼1090倍。平坦、歐幾里得、膨脹宇宙的度量表示為:
$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$
我們希望將度量寫入任何曲率。
羅伯遜和沃克證明了對於任何曲率宇宙(它是均勻且各向同性的),度量表示為:
$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$
這通常被稱為羅伯遜-沃克度量(Robertson–Walker Metric),適用於任何空間拓撲。請注意$dr^2$中的額外因子。這裡的𝑘是曲率常數。
宇宙的幾何形狀
宇宙的幾何形狀藉助以下曲率來解釋,其中包括:
- 正曲率
- 負曲率
- 零曲率
讓我們詳細瞭解每一個。
正曲率
如果在曲率曲面上任意一點繪製的切平面不與曲面上的任何點相交,則該曲面稱為正曲率曲面,即曲面始終位於該點的切平面的同一側。球面具有正曲率。
負曲率
如果在曲率曲面上某一點繪製的切平面與曲面上的任何點相交,則該曲面稱為負曲率曲面,即曲面在兩個不同的方向上遠離切平面彎曲。馬鞍形曲面具有負曲率。
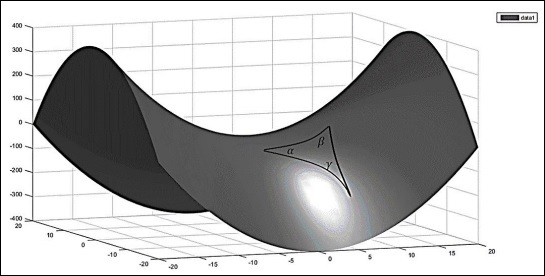
現在考慮球面。如果透過連線三個點用測地線(大圓弧)在球面上構造一個三角形,則球面三角形的內角和大於 180o,即 −
$$\alpha + \beta + \gamma > \pi$$
這樣的空間稱為正曲率空間。此外,曲率是均勻且各向同性的。一般來說,球面三角形頂點的角度遵循以下關係 −
$$\alpha + \beta +\gamma = \pi + A/R^2$$
其中A是三角形的面積,R是球體的半徑。下圖描繪了一個正曲率空間。
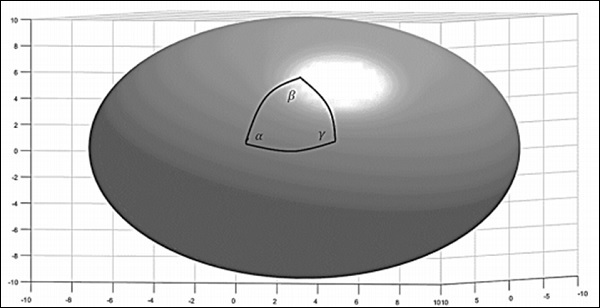
對於正曲率,平行線應該相交。考慮地球表面,它是一個正曲率空間。在地球赤道上取兩個起點。垂直於赤道穿過赤道的線被稱為經線。由於這些線垂直於赤道相交,因此可以將它們稱為平行線。從赤道開始,它們最終在兩極相交。這種方法被卡爾·高斯等人用來理解地球的拓撲結構。
考慮一個負曲率空間(下圖所示的馬鞍),三角形的內角和小於 180o,即 −
$$\alpha + \beta + \gamma < \pi$$
頂點的角度遵循以下關係 −
$$\alpha + \beta + \gamma = \pi - A/R^2$$
零曲率
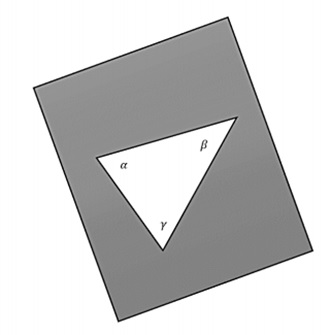
平面曲面具有零曲率。現在對於一個平面空間,如果取一個平面並透過用測地線(直線)連線三個點來構造一個三角形,則內角和將為 −
$$\alpha + \beta + \gamma = \pi$$
下圖是一個平坦的二維空間。
如果想要一個均勻且各向同性的空間,則只剩下三種可能性:空間可以是均勻平坦的,也可以具有均勻的正曲率,或者可以具有均勻的負曲率。
曲率常數可以取以下三個值中的任何一個。
$$k = \begin{cases}+1, & 正曲率空間;\\\quad 0, & 平坦空間; \\-1, & 負曲率空間;\end{cases}$$
宇宙的全域性拓撲結構
宇宙具有一定的拓撲結構,但在區域性可能存在褶皺。根據物質在空間中的分佈情況,曲率存在較小的變化。讓我們假設有一類物體,無論它位於宇宙中的哪個位置,其真實大小都相同,這意味著它們就像標準燭光一樣。它們的亮度不同,但大小相同。
如果物體位於正曲率空間中,並且光子來自點 A(物體的一端)和點 B(物體的另一端),則光子將在正曲率空間中沿測地線路徑平行傳播,並最終相遇。對於 C 點的觀察者來說,它似乎來自不同方向的兩個不同點。
如果物體位於區域性宇宙中,我們測量角大小,它不受曲率的影響。如果在更大的紅移處看到同一類物體,則角大小與之不相關。
$$\theta = \frac{d}{r}$$
其中d是物體的尺寸,r是到物體的距離,即如果尺寸大於區域性尺寸,則意味著曲率為正。下圖是正曲率空間中檢測到的光子的表示。
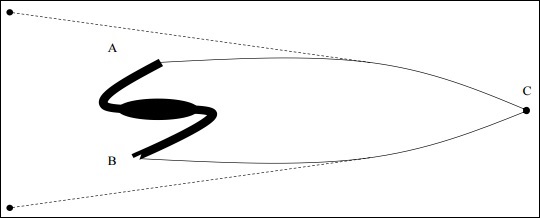
需要注意的是,沒有真正具有標準尺寸和形態的天體物理物體。雖然人們認為巨大的橢圓cD星系符合標準燭光的標準,但後來發現它們也隨時間演化。
尋找星系的距離
在本節中,我們將討論如何透過考慮下圖來找到星系的距離。
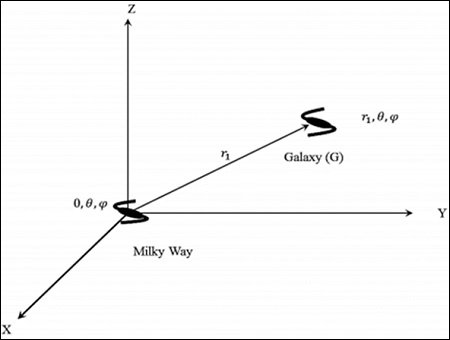
在宇宙靜止參考系中考慮位於 (r, θ,) 的銀河系。可以透過呼叫均勻性假設來取 𝑟 = 0; (0, θ,ϕ),即宇宙的中心。
考慮位於 (r1, θ,) 的星系“G”。距離(固有距離)是光子傳播的最短徑向距離。根據時空的對稱性,從 r = 0 到 r = r1 的零測地線在空間中具有恆定的方向。在其徑向傳播中,角度座標不會改變。如果角度座標發生改變,則它不是最短路徑。這就是為什麼曲率項存在於 dr2 中的原因。
要點
宇宙的膨脹是向所有方向的。
宇宙可以是靜態的、膨脹的或收縮的,這取決於比例因子的演化。
cD星系會隨時間演化,因此不能用作標準燭光。
宇宙具有一定的拓撲結構,但在區域性可能存在褶皺。
哈勃引數與比例因子
本章將討論哈勃引數和比例因子。
先決條件 − 宇宙紅移,宇宙原理。
假設 − 宇宙是均勻且各向同性的。
哈勃常數與比例因子變化率的關係
在本節中,我們將哈勃常數與比例因子變化率聯絡起來。
我們可以用以下方式寫出速度並簡化。
$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$
$$= \frac{d[a(t)r_c}{dt}$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$
這裡,v是退行速度,a是比例因子,rp是星系之間的固有距離。
哈勃經驗公式的形式為 −
$$v = H \ast r_p$$
因此,比較上述兩個方程,我們得到 −
哈勃引數 = 比例因子的變化率
$$H = da/dt \ast 1/a$$
注意 − 這不是一個常數,因為比例因子是時間的函式。因此它被稱為哈勃引數,而不是哈勃常數。
經驗上我們寫 −
$$H = V/D$$
因此,從這個方程中,我們可以推斷,由於D在增加而V是一個常數,那麼H隨著時間的推移和宇宙的膨脹而減小。
弗裡德曼方程與羅伯遜-沃克模型結合
在本節中,我們將瞭解弗裡德曼方程如何與羅伯遜-沃克模型結合使用。為了理解這一點,讓我們以以下影像為例,該影像中有一個距離為rp的試驗質量與質量為M的天體。
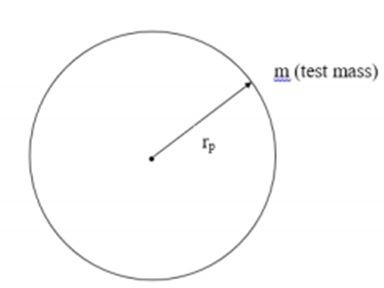
考慮到上圖,我們可以將力表示為 −
$$F = G \ast M \ast \frac{m}{r^2_p}$$
這裡,G是萬有引力常數,ρ是可觀測宇宙內的物質密度。
現在,假設球體內質量密度均勻,我們可以寫 −
$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$
將這些代回到我們的力方程中,我們得到 −
$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$
因此,我們可以將質量m的勢能和動能寫為 −
$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$
$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$
使用維裡定理 −
$$U = K.E + V$$
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
但是這裡,$r_p = ar_c$。所以我們得到 −
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
進一步簡化後,我們得到弗裡德曼方程,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$
這裡U是一個常數。我們還注意到,我們目前生活的宇宙是由物質主導的,而輻射能量密度非常低。
要點
哈勃引數隨著時間的推移和宇宙的膨脹而減小。
我們目前生活的宇宙是由物質主導的,輻射能量密度非常低。
弗裡德曼方程與宇宙模型
本章將瞭解弗裡德曼方程是什麼,並詳細研究不同曲率常數的世界模型。
弗裡德曼方程
該方程告訴我們關於宇宙均勻且各向同性模型中空間膨脹的資訊。
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{2U}{mr_c^2a^2}$$
這在廣義相對論(GR)和羅伯遜-沃克度規的背景下進行了修改,如下所示。
使用 GR 方程 −
$$\frac{2U}{mr_c^2} = -kc^2$$
其中k是曲率常數。因此,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}$$
此外,ρ被能量密度取代,其中包括物質、輻射和任何其他形式的能量。但出於表示目的,它寫成ρ。
不同曲率常數的世界模型
現在讓我們根據曲率常數值檢視各種可能性。
情況 1:k=1,或封閉宇宙
對於膨脹宇宙,$da/dt > 0$。隨著膨脹繼續,上述方程右側的第一項為 $a^{-3}$,而第二項為 $a^{-2}$。當這兩項相等時,宇宙停止膨脹。然後 −
$$\frac{8 \pi G}{3}\rho = \frac{kc^2}{a^2}$$
這裡,k=1,因此,
$$a = \left [ \frac{3c^2}{8 \pi G\rho} \right ]^{\frac{1}{2}}$$
這樣的宇宙是有限的,並且體積有限。這被稱為封閉宇宙。
情況 2:k=-1,或開放宇宙
如果k < 0,膨脹將永遠不會停止。在某個時刻,與第二項相比,可以忽略右側的第一項。
這裡,k = -1。因此,$da/dt ∼ c$。
在這種情況下,宇宙正在勻速運動。這樣的宇宙具有無限的空間和時間。這被稱為開放宇宙。
情況 3:k=0,或平坦宇宙
在這種情況下,宇宙以減小的速度膨脹。這裡,k = 0。因此,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho$$
這樣的宇宙具有無限的空間和時間。這被稱為平坦宇宙。
要點
弗裡德曼方程告訴我們關於宇宙均勻且各向同性模型中空間膨脹的資訊。
根據不同的曲率常數值,我們可以擁有封閉宇宙、開放宇宙或平坦宇宙。
宇宙學 - 流體方程
本章將討論流體方程以及它如何告訴我們宇宙的密度隨時間變化。
估計當前宇宙中的ρc和ρ
對於當前宇宙 −
$$\rho_c \simeq 10^{11}M_\odot M_{pc}^{-3} \simeq 10\: 氫原子 \: m^{-3}$$
宇宙空間存在著各種各樣的臨界密度。例如,星系際介質的臨界密度ρc為每立方米1個氫原子,而分子云的臨界密度則為每立方米10⁶個氫原子。
我們必須考慮適當的空間樣本測量ρc。在我們的星系內,ρc的值非常高,但我們的星系並不能代表整個宇宙。因此,我們應該到宇宙學原理成立的宇宙空間中去,即距離≈300 Mpc。觀察300 Mpc意味著回溯10億年前,但這仍然是現在的宇宙。
像SDSS這樣的巡天調查被用來確定實際的物質密度。它們選取一個5×500×5 Mpc³的體積,計算星系數量,並累加來自這些星系的所有光線。假設1 L ≡ 1 M,即1個太陽光度≡1個太陽質量。
我們進行光到質量的轉換,然後嘗試根據該體積中存在的可見物質粒子來估計重子數。
例如:
$$1000L_\odot ≡ 1000M_\odot / m_p$$
其中,mp=質子質量。
然後我們得到大約的重子數密度Ωb ≈ 0.025。這意味著ρb = ρc的0.25%。不同的調查結果略有不同。因此,在區域性宇宙中,可見物質的數密度遠小於臨界密度,這意味著我們生活在一個開放的宇宙中。
這些調查沒有包含質量因數為10的物質,因為這些調查考慮的是電磁輻射,而不是暗物質。因此,Ωm = 0.3 - 0.4。這仍然得出我們生活在一個開放宇宙中的結論。
暗物質與引力相互作用。大量的暗物質可以阻止宇宙膨脹。我們還沒有確定ρ如何隨時間變化,這需要另一組方程。
熱力學指出:
$$dQ = dU + dW$$
對於一個體積增長的系統,dW = P dV。宇宙的膨脹被建模為絕熱的,即dQ = 0。因此,體積變化應該來自內能的變化dU。
讓我們取一定體積的宇宙,其共動半徑為單位,即rc = 1。如果ρ是該空間體積內物質的密度,則:
$$M = \frac{4}{3} \pi a^3r_c^3 \rho$$
$$U = \frac{4}{3}\pi a^3\rho c^2$$
其中,**U**是能量密度。讓我們找出宇宙膨脹時內能隨時間的變化。
$$\frac{\mathrm{d} U}{\mathrm{d} t} = 4 \pi a^2 \rho c^2 \frac{\mathrm{d} a}{\mathrm{d} t} + \frac{4}{3}\pi a^3 c^2\frac{\mathrm{d} \rho}{\mathrm{d} t}$$
同樣,體積隨時間的變化由下式給出:
$$\frac{\mathrm{d} V}{\mathrm{d} t} = 4\pi a^2 \frac{\mathrm{d} a}{\mathrm{d} t}$$
代入dU = −P dV。我們得到:
$$4\pi a^2(c^2 \rho +P)\dot{a}+\frac{4}{3}\pi a^3c^2\dot{\rho} = 0$$
$$\dot{\rho}+3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
這被稱為**流體方程**。它告訴我們宇宙的密度如何隨時間變化。
宇宙膨脹時壓力下降。在每一時刻壓力都在變化,但在所考慮的體積內兩點之間沒有壓力差,因此壓力梯度為零。只有相對論物質才會產生壓力,物質本身沒有壓力。
弗裡德曼方程與流體方程一起模擬宇宙。
要點
暗物質與引力相互作用。大量的暗物質可以阻止宇宙膨脹。
流體方程告訴我們宇宙的密度如何隨時間變化。
弗裡德曼方程與流體方程一起模擬宇宙。
只有相對論物質才會產生壓力,物質本身沒有壓力。
宇宙學 - 物質主導宇宙
在本章中,我們將討論與物質主導宇宙相關的弗裡德曼方程的解。在宇宙學中,因為我們在大尺度上觀察一切,太陽系、星系,所有的一切都像塵埃粒子一樣(這就是我們用肉眼看到的樣子),我們可以稱之為塵埃宇宙或僅物質宇宙。
在**流體方程**中:
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$
我們可以看到存在一個壓力項。對於塵埃宇宙,**P = 0**,因為物質的能量密度將大於輻射壓力,並且物質沒有以相對論速度運動。
因此,流體方程將變為:
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$
$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$
$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$
$$\Rightarrow \rho a^3 =\: 常數$$
$$\Rightarrow \rho \propto \frac{1}{a^3}$$
這個方程沒有違反直覺,因為密度應該按a⁻³縮放,因為體積隨a³增加。
從最後一個關係,我們可以說:
$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$
對於現在的宇宙,a等於a₀,應該為1。因此:
$$\rho(t) = \frac{\rho_0}{a^3}$$
在物質主導的平坦宇宙中,k = 0。因此,弗裡德曼方程將變為:
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$
$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$
透過求解這個方程,我們將得到:
$$a \propto t^{2/3}$$
$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$
$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$
這意味著宇宙將以減小的速度持續膨脹。下圖顯示了塵埃宇宙的膨脹。
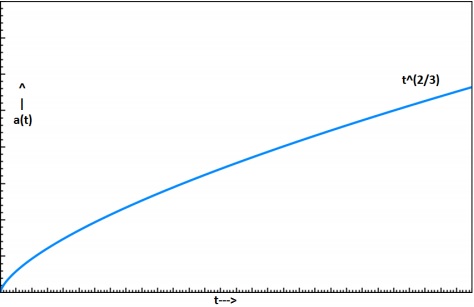
ρ如何隨時間變化?
看看下面的方程:
$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$
我們知道比例因子隨時間變化為t²/³。因此:
$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$
對其求導,我們將得到:
$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$
我們知道**哈勃常數**是:
$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$
這是**愛因斯坦-德西特宇宙**的方程。如果我們想計算宇宙的當前年齡,那麼:
$$t_0 = t_{年齡} = \frac{2}{3H_0}$$
代入當前宇宙的H₀值後,我們將得到宇宙年齡的值為**90億年**。在我們自己的銀河系中,有很多**球狀星團**的年齡超過這個值。
這就是關於塵埃宇宙的全部內容。現在,如果您假設宇宙是由輻射而不是物質主導的,那麼輻射能量密度將隨a⁻⁴變化,而不是a⁻³。我們將在下一章中詳細討論。
要點
在宇宙學中,所有的一切都像塵埃粒子一樣,因此,我們稱之為塵埃宇宙或僅物質宇宙。
如果我們假設宇宙是由輻射而不是物質主導的,那麼輻射能量密度將隨a⁻⁴變化,而不是a⁻³。
宇宙學 - 輻射主導宇宙
在本章中,我們將討論與輻射主導宇宙相關的弗裡德曼方程的解。首先,我們將比較物質的能量密度與輻射的能量密度。這將使我們能夠判斷我們的宇宙是物質主導的還是輻射主導的。
輻射能量密度
當前宇宙中普遍存在的輻射很少歸因於恆星源,但主要歸因於殘餘的CMB(宇宙微波背景)。
輻射的能量密度εγ,0可以表示如下:
$$\epsilon_{\gamma,0} = aT_0^4$$
這裡,**a**是輻射常數,其表示式為(8π⁵kB⁴)/(15h³c²) 等於 **a = 7.5657 × 10⁻¹⁵ erg cm⁻³ K⁻⁴**。我們在這裡考慮的溫度T₀對應於CMB的黑體溫度。
代入結果,我們有:
$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$
物質能量密度
在下述計算中,我們假設使用平坦宇宙且K = 0。我們將物質的能量密度考慮為ε = ρc²。我們考慮以下內容:
$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$
$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$
因此,從上述計算中,我們看到我們生活在一個物質主導的宇宙中。這可以從CMB非常冷的事實得到支援。當我們回溯時間時,CMB溫度會變得越來越熱,並且能夠得出結論,可能存在一個宇宙由輻射主導的時期。
密度和比例因子的變化
流體方程向我們展示了:
$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
如果我們考慮塵埃宇宙,我們將有P = 0。撇開之前的結果,我們將宇宙視為由輻射主導的。
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$
使用壓力關係Prad = ρc²/3,我們有:
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$
$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$
進一步簡化,我們有:
$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$
$$\rho_{rad}a^4 =\: 常數$$
$$\rho_{rad} \propto \frac{1}{a^4}$$
上述結果顯示a與ρ的-4次方反比變化。
這可以在物理上解釋為體積變化帶來的a⁻³。剩餘的a⁻¹可以被視為由於宇宙空間膨脹而導致光子損失的能量(宇宙紅移1 + z = a⁻¹)。
下圖顯示了物質和輻射密度隨時間的變化。
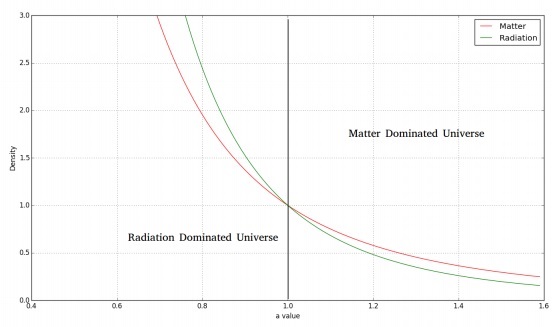
對於平坦的輻射主導宇宙,弗裡德曼方程如下:
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$
簡化並應用微分方程的解,我們有:
$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$
$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$
因此,我們有:
$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$
從上述方程,我們看到比例因子的增長率小於塵埃宇宙。
要點
當前宇宙中普遍存在的輻射很少歸因於恆星源。
對於塵埃宇宙,壓力為零。
CMB非常冷。
宇宙學 - 暗能量
暗能量領域在天文學中是一個非常模糊的領域,因為它在所有方程中都是一個自由引數,但對其究竟是什麼並沒有明確的概念。
我們將從弗裡德曼方程開始:
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$
大多數關於宇宙學的入門書籍,它們都從哈勃觀測之前的宇宙是封閉且靜止的這一事件開始描述暗能量。
為了使宇宙在右側保持靜態,這兩個項必須相等且都為零。但如果第一項大於第二項,宇宙將不會是靜態的。因此,愛因斯坦在場的方程中引入了自由引數∧來使宇宙靜態。他認為,無論第一項與第二項相比如何,只要方程中多出一個分量來補償這兩個項之間的差異,就能始終得到一個靜態的宇宙。
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$
$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$
其中 $P = \rho \ast c^2/3$ 且 $\wedge = \rho \ast c^2$ 是宇宙學常數。(負號僅因萬有引力吸引作用)
在上式(加速度方程)中:
$3P/c^2$ 是由於輻射引起的負壓,
$-4\pi G/3$ 是由於萬有引力引起的吸引力,
$\wedge/3$ 作出正貢獻。
第三項起斥力的作用,因為方程的另一部分是吸引力。
該方程的物理意義在於˙a = 0,因為當時沒有任何證據表明宇宙正在膨脹。如果這兩個項不匹配,那麼最好新增一個分量,並根據偏移量來改變自由引數的值。
當時對這個宇宙學常數沒有物理學解釋,這就是為什麼當宇宙膨脹的解釋在20世紀20年代被發現時,愛因斯坦不得不立即拋棄這個常數的原因。
這個宇宙學常數的解釋仍在使用,因為它解釋了宇宙的不同版本,但這個宇宙學常數的定義和解釋方式隨著時間的推移而不斷變化。
現在,由於許多原因,宇宙學常數的概念又被帶回了宇宙學。其中一個原因是,我們對宇宙不同成分(重子物質、暗物質、輻射)的能量密度有了觀測資料,所以我們知道這個引數是什麼。利用宇宙微波背景輻射的獨立觀測表明 k=0。
$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: 氫原子.m^{-3}$$
為了使 k 為 0,ρ 應該等於 ρc,但我們知道,如果將所有已知成分加起來,結果不等於 0,這意味著存在某種其他成分,其值遠小於 ρc。
$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$
暗能量的另一個證據來自Ia型超新星觀測,Ia型超新星發生在白矮星吸積物質並超過錢德拉塞卡極限(≈ 1.4M)時。每次Ia型超新星爆發時,其質量都相同,這意味著系統的總結合能相同,我們能夠看到的可見光能量也相同。
當然,超新星的光度會先增強然後減弱,但如果你測量峰值亮度,它總是相同的,這使其成為一個標準的候選者。因此,利用Ia型超新星,我們可以測量宇宙的宇宙學分量,天文學家發現,高紅移的超新星比低紅移的超新星暗 30%−40%,如果存在非零的∧項,就可以解釋這種現象。
在宇宙學模型中,DE(暗能量)被視為一種流體,這意味著我們可以寫出它的狀態方程。狀態方程是連線物質兩種不同狀態的變數(如壓力、密度、溫度和體積)的方程。
從量綱上看,
$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$
$$\rho_\wedge = \frac{\wedge}{8\pi G}$$
暗能量的能量密度為:
$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$
暗能量密度引數為:
$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$
Ω∧是暗能量密度與臨界密度之比。
$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$
關於暗能量有很多理論,暗能量正在排斥宇宙並導致宇宙膨脹。一個假設是,暗能量可能是真空能量密度。假設空間本身正在產生某種能量,當你計算空間單位體積內重子物質、暗物質和輻射的能量時,你也在計算與空間相關的能量,但這並不清楚暗能量是否真的是真空能量密度。
我們知道暗物質和輻射的密度與比例因子之間的關係是:
$$\rho_m \propto \frac{1}{a^3}$$
$$\rho_m \propto \frac{1}{a^4}$$
我們有密度與比例因子的關係圖。在同一圖中,我們可以看到ρ∧隨著宇宙膨脹是一個常數,不依賴於比例因子。
下圖顯示了密度和比例因子之間的關係。
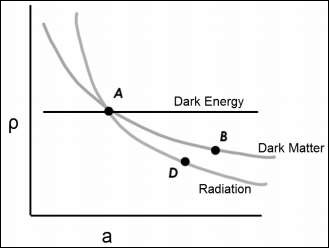
‘ρ’ 與 ‘a’(比例因子與時間有關)在同一圖中,暗能量被建模為常數。因此,無論我們在當前宇宙中測量到多少暗能量,它都是一個常數。
要點
利用宇宙微波背景輻射的獨立觀測表明 k=0。
ρ∧隨著宇宙膨脹是一個常數,不依賴於比例因子。
引力也隨時間變化,這被稱為修正牛頓動力學。
宇宙學 - 螺旋星系旋轉曲線
本章將討論螺旋星系旋轉曲線以及暗物質的證據。
暗物質和關於暗物質的觀測事實
暗物質的早期證據是對螺旋星系運動學的研究所得。
太陽距我們銀河系的中心偏移了3萬光年。銀心速度為220公里/秒。
為什麼速度是220公里/秒而不是100公里/秒或500公里/秒?是什麼控制著天體的圓周運動?
半徑內包含的質量有助於探測宇宙中的速度。
銀河系或螺旋星系的旋轉 - 微分旋轉
角速度隨距中心的距離而變化。
軌道週期取決於距中心的距離。
靠近銀河系中心的物質週期較短,遠離銀河系中心的物質週期較長。
旋轉曲線
預測速度隨銀心半徑的變化。該曲線給出了速度隨軌道半徑的變化。
當我們看到物體運動時,我們認為是引力影響了旋轉。
質量分佈隨半徑而變化。物質密度將預測旋轉曲線。基於隨半徑變化的物質密度的旋轉曲線。
表面亮度
我們選擇一個區域,看看有多少光發出。
從該區域發出的光量稱為表面亮度。
其單位為mag/arcsec2。
如果我們發現表面亮度隨半徑變化,我們可以發現發光物質隨半徑變化。
$$\mu(r) \propto exp \left( \frac{-r}{h_R} \right )$$
$h_R$ 是尺度長度。$\mu(r) = \mu_o \ast exp \left( \frac{-r}{h_R} \right )$
$h_R$ 對於銀河系來說大約是 3 kpc。
螺旋星系
為了理解旋轉曲線,天文學家將星系分成兩個部分:
- 盤
- 核球
下圖顯示了一箇中心球形核球+圓盤。核球和盤中的恆星和氣體分佈不同。
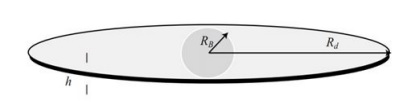
螺旋星系的運動學
-
任何物體的圓周速度 - 對於核球 (r < Rb)。
$$V^2(r) = G \ast \frac{M(r)}{r}$$
$$M(r) = \frac{4\pi r^3}{3} \ast \rho_b$$
-
對於盤 - (Rb < r < Rd)
$$V^2(r) = G \ast \frac{M(r)}{r}$$
核球具有大致恆定的恆星密度。
核球內的密度是恆定的(在核球內的距離不隨距離變化)。
在盤中,恆星密度隨半徑減小。半徑增加,發光物質減少。
在核球中 - $V(r) \propto r$
在盤中 - $V(r) \propto 1/\sqrt{r}$
螺旋星系的旋轉曲線
透過光譜學(附近的星系 - 空間分辨星系),我們繪製了旋轉曲線。
如上所述,我們看到旋轉曲線在外區是平坦的,即外區物體運動速度很快,這通常不是這種形式。
軌道速度隨著內區半徑的增加而增加,但在外區變平。
暗物質
暗物質被認為是宇宙的非發光成分。讓我們透過以下幾點來了解暗物質。
平坦的旋轉曲線與我們在螺旋星系中看到的恆星和氣體分佈相反。
盤的表面光度隨半徑呈指數下降,這意味著發光物質(主要是恆星)的質量集中在銀河系中心附近。
旋轉曲線的平坦化表明,在一定半徑r內星系的總質量總是隨著r的增加而增加。
這隻有在這些星系中存在大量看不見的具有引力的物質,並且不發出電磁輻射的情況下才能解釋。
螺旋星系的旋轉曲線測量是暗物質最令人信服的證據之一。
暗物質的證據
缺失質量 - 發光質量的 10 倍。
大部分暗物質必須位於星系的暈中:盤中大量暗物質會擾亂盤對抗潮汐力的長期穩定性。
盤中一小部分暗物質可能是重子物質 - 暗淡的恆星(褐矮星、黑矮星)和緻密的恆星殘餘物(中子星、黑洞)。但這種重子暗物質無法解釋星系中缺失質量的全部規模。
暗物質的密度剖面 - $M(r) \propto r$ 和 $\rho(r) \propto r^{−2}$。
螺旋星系的旋轉曲線資料與分佈在其暈中的暗物質一致。
這個暗暈構成了星系大部分的總質量。
所有重子物質(恆星、星團、星際介質等)都由這個暗物質暈的引力勢束縛在一起。
結論
暗物質只通過其與普通物質的引力相互作用被探測到。尚未觀測到其與光(無電磁力)的相互作用。
中微子——無電荷,弱相互作用,但質量太小(< 0.23 eV)。為了解釋結構的形成,暗物質粒子應該具有 E > 10 eV 左右的能量。
弱相互作用大質量粒子 (WIMP) 可能是暗物質的來源。
要點
靠近銀河系中心處的物質具有較短的週期。
核球具有大致恆定的恆星密度。
星盤的表面光度隨半徑呈指數下降。
星盤中大量的暗物質可能會擾亂星盤抵抗潮汐力的長期穩定性。
星系速度彌散測量
暗物質的第一個直接證據來自弗裡茨·茲威基 (Fritz Zwicky)。他進行了一些觀測,首次揭示了暗物質的存在。他的觀測考慮了星系團內的整體運動。
擴充套件的天體是星系團,它們被認為是束縛結構。這些星系相對於星系團中心運動,但不會飛散出去。我們觀察星系的整體運動。
假設:速度代表潛在的潛在能量
每個星系在星系團內都有其自身的自行運動和哈勃流分量。較小的星系較小,大部分光來自M31和銀河系,還有幾個矮星系。對於我們的粗略分析,我們只能使用M31和銀河系來評估本星系群的動力學質量。
我們和M31之間存在相對速度。這很粗略,但它是真實的。故事開始很久以前,那時M31和銀河系彼此靠近,因為它們都是一個星系團的成員,它們彼此遠離。一段時間後,它們達到最大分離距離,然後彼此靠近。
讓我們假設它們所能達到的最大分離距離為$r_{max}$。現在它們的分離距離稱為r。設M為M31和銀河系的總質量。我們不知道$r_{max}$何時達到。
$$ \frac{GM}{r_{max}} = 在r_{max}處的勢能 $$
當這些星系在某一時刻r彼此靠近時,系統的能量將為:
$$ \frac{1}{2}\sigma^2 = \frac{GM}{r} = \frac{GM}{r_{max}} $$
σ是兩個星系的相對速度。M只是約化質量,但檢驗質量為1。σ是距離星團中心r處任何物體的速度。我們相信這個星團處於動態平衡狀態,因為維裡定理成立。因此,星系不能以不同的速度運動。
這些星系需要多長時間才能達到最大距離?
為了理解這一點,讓我們考慮以下方程:
$$ \frac{1}{2}\left ( \frac{dr}{dt} \right )^2 = \frac{GM}{r} - \frac{GM}{r_{max}} $$
$$ t_{max} = \int_{0}^{r_{max}} dt = \int_{0}^{r_{max}} \frac{dr}{\sqrt{2GM}}\left ( \frac{1}{r} - \frac{1}{r_{max}} \right )^2 $$
$$ t_{max} = \frac{\pi r_{max}^{\frac{3}{2}}}{2\sqrt{2GM}} $$
其中,M = 本星系群的動力學質量。從碰撞開始到結束的總時間為$2t_{max}$。因此,
$$ 2t_{max} = t_0 + \frac{D}{\sigma} $$
而$t_0$是宇宙的當前年齡。
如果實際的$t_{max} < 右側值$,那麼我們就有時間的下限。$D/\sigma$是它們再次碰撞的時間。這裡,我們假設σ是常數。
$$ t_{max} = \frac{t_0}{2} + \frac{D}{2\sigma} $$
$$ r_{max} = t_{max} \times \sigma = 770K_{pc} $$
這裡,σ = 銀河系和M31之間的相對速度。
$$ M_{dynamic} = 3 \times 10^{12}M_0 $$
$$ M_{MW}^{lum} = 3 \times 10^{10}M_0 $$
$$ M_{M31}^{lum} = 3 \times 10^{10}M_0 $$
但實際上,動力學質量是考慮星系團內每個星系計算出來的。缺失的質量就是暗物質,而弗裡茨·茲威基 (Fritz Zwicky)注意到后髮座星系團中的星系運動速度太快。他預測了中子星存在的可能性,僅僅在中子星被發現的第二年,他利用帕洛瑪天文臺尋找超新星。
要點
暗物質的第一個直接證據來自弗裡茨·茲威基 (Fritz Zwicky)。
擴充套件的天體是星系團,它們被認為是束縛結構。
動力學質量是考慮星系團內每個星系計算出來的。
宇宙學 - 哈勃引數和密度引數
本章將討論密度引數和哈勃引數。
哈勃引數
哈勃引數定義如下:
$$ H(t) \equiv \frac{da/dt}{a} $$
它衡量比例因子變化的速度。更一般地說,比例因子的演化由弗裡德曼方程決定。
$$ H^2(t) \equiv \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{kc^2}{a^2} + \frac{\wedge}{3} $$
其中,∧是宇宙常數。
對於平坦宇宙,k = 0,因此弗裡德曼方程變為:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{\wedge}{3} $$
對於物質主導的宇宙,密度變化如下:
$$ \frac{\rho_m}{\rho_{m,0}} = \left ( \frac{a_0}{a} \right )^3 \Rightarrow \rho_m = \rho_{m,0}a^{-3} $$
而對於輻射主導的宇宙,密度變化如下:
$$ \frac{\rho_{rad}}{\rho_{rad,0}} = \left ( \frac{a_0}{a} \right )^4 \Rightarrow \rho_{rad} = \rho_{rad,0}a^{-4} $$
目前,我們生活在一個物質主導的宇宙中。因此,考慮$\rho \equiv \rho_m$,我們得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{\wedge}{3} $$
宇宙常數和暗能量密度關係如下:
$$ \rho_\wedge = \frac{\wedge}{8 \pi G} \Rightarrow \wedge = 8\pi G\rho_\wedge $$
由此,我們得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{8 \pi G}{3} \rho_\wedge $$
此外,臨界密度和哈勃常數關係如下:
$$ \rho_{c,0} = \frac{3H_0^2}{8 \pi G} \Rightarrow \frac{8\pi G}{3} = \frac{H_0^2}{\rho_{c,0}} $$
由此,我們得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{H_0^2}{\rho_{c,0}}\rho_{m,0}a^{-3} + \frac{H_0^2}{\rho_{c,0}}\rho_\wedge $$
$$ \left ( \frac{\dot{a}}{a} \right )^2 = H_0^2\Omega_{m,0}a^{-3} + H_0^2\Omega_{\wedge,0} $$
$$ (\dot{a})^2 = H_0^2\Omega_{m,0}a^{-1} + H_0^2\Omega_{\wedge,0}a^2 $$
$$ \left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}\frac{1}{a} + \Omega_{\wedge,0}a^2 $$
$$ \left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}(1+z) + \Omega_{\wedge,0}\frac{1}{(1+z)^2} $$
$$ \left ( \frac{\dot{a}}{H_0} \right)^2 (1+z)^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0} $$
$$ \left ( \frac{\dot{a}}{H_0} \right)^2 \frac{1}{a^2} = \Omega_{m,0}(1 + z)^3 + \Omega_{\wedge,0} $$
$$ \left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0} $$
這裡,$H(z)$是紅移相關的哈勃引數。這可以修改為包含輻射密度引數$\Omega_{rad}$和曲率密度引數$\Omega_k$。修改後的方程為:
$$ \left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4+\Omega_{k,0}(1+z)^2+\Omega_{\wedge,0} $$
$$ 或,\left ( \frac{H(z)}{H_0} \right)^2 = E(z) $$
$$ 或,H(z) = H_0E(z)^{\frac{1}{2}} $$
其中,
$$ E(z) \equiv \Omega_{m,0}(1 + z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2+\Omega_{\wedge,0} $$
這表明哈勃引數隨時間變化。
對於愛因斯坦-德西特宇宙,$\Omega_m = 1, \Omega_\wedge = 0, k = 0$。
將這些值代入,我們得到:
$$ H(z) = H_0(1+z)^{\frac{3}{2}} $$
這顯示了愛因斯坦-德西特宇宙中哈勃引數的時間演化。
密度引數
密度引數$\Omega$定義為實際(或觀測到的)密度ρ與臨界密度$\rho_c$的比率。對於任何量$x$,相應的密度引數$\Omega_x$可以用數學方式表示為:
$$ \Omega_x = \frac{\rho_x}{\rho_c} $$
對於正在考慮的不同量,我們可以定義以下密度引數。
| 序號 | 數量 | 密度引數 |
|---|---|---|
| 1 | 重子 | $\Omega_b = \frac{\rho_b}{\rho_c}$ |
| 2 | 物質(重子+暗物質) | $\Omega_m = \frac{\rho_m}{\rho_c}$ |
| 3 | 暗能量 | $\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$ |
| 4 | 輻射 | $\Omega_{rad} = \frac{\rho_{rad}}{\rho_c}$ |
其中符號具有其通常的含義。
要點
比例因子的演化由弗裡德曼方程決定。
H(z)是紅移相關的哈勃引數。
哈勃引數隨時間變化。
密度引數定義為實際(或觀測到的)密度與臨界密度的比率。
宇宙學 - 宇宙年齡
如前幾章所述,哈勃引數的時間演化由下式給出:
$$ H(z) = H_0E(z)^{\frac{1}{2}} $$
其中z是紅移,E(Z)為:
$$ E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega(1+z)^4 +\Omega_{k,0}(1+z)^2 + \Omega^{\wedge,0} $$
如果宇宙的膨脹是恆定的,那麼宇宙的真實年齡如下:
$$ t_H = \frac{1}{H_0} $$
如果是物質主導的宇宙,即愛因斯坦-德西特宇宙,那麼宇宙的真實年齡由下式給出:
$$ t_H = \frac{2}{3H_0} $$
比例因子和紅移由下式定義:
$$ a=\frac{a_0}{1+z} $$
宇宙年齡根據宇宙學引數的推導如下。
哈勃引數由下式給出:
$$ H = \frac{\frac{da}{dt}}{a} $$
求導,我們得到:
$$ da = \frac{-dz}{(1+z)^2} $$
其中a0 = 1(比例因子的當前值)
$$ \frac{\mathrm{d} a}{\mathrm{d} t} = \frac{-1}{(1+z)^2} $$
$$ \frac{\mathrm{d} a}{\mathrm{d} t} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} $$
$$ H = \frac{\dot{a}}{a} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} \frac{1+z}{1} $$
$$ \frac{\dot{a}}{a} = \frac{-1}{1+z}\frac{\mathrm{d} z}{\mathrm{d} t}\frac{1}{1} $$
$$ H(z) = H_0E(z)^{\frac{1}{2}} $$
$$ dt = \frac{-dz}{H_0E(z)^{\frac{1}{2}}(1+z)} $$
如果我們想找到宇宙在任何給定紅移'z'時的年齡,那麼:
$$ t(z) = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz $$
其中k是曲率密度引數,並且:
$$ E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2 + \Omega_{\wedge,0} $$
要計算宇宙當前的年齡,取z1 = 0。
$$ t(z=0) = t_{age} = t_0 = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz $$
對於愛因斯坦-德西特模型,即$\Omega_m = 1$,$\Omega_{rad} = 0$,$\Omega_k = 0$,$\Omega_\wedge = 0$,宇宙年齡的方程變為:
$$ t_{age} = \frac{1}{H_0}\int_{0}^{\infty} \frac{1}{(1+z)^{\frac{5}{2}}}dz $$
求解積分後,我們得到:
$$ t_H = \frac{2}{3H_0} $$
夜空就像一臺宇宙時間機器。每當我們觀測遙遠的行星、恆星或星系時,我們看到的都是它在數小時、數百年甚至數千年前的樣子。這是因為光以有限的速度(光速)傳播,並且考慮到宇宙中的巨大距離,我們看到的不是物體現在的樣子,而是光發射時它們的樣子。在我們在地球上探測到光線和它最初由光源發射之間經過的時間被稱為回溯時間 (tL(z1))。
因此,回溯時間由下式給出:
$$ t_1(z_1) = t_0-t(z_1) $$
愛因斯坦-德西特宇宙的回溯時間為:
$$ t_L(z) = \frac{2}{3H_0}\left [ 1- \frac{1}{(1+z)^{\frac{3}{2}}} \right ] $$
要點
每當我們觀測遙遠的行星、恆星或星系時,我們看到的都是它在數小時、數百年甚至數千年前的樣子。
在我們在地球上探測到光線和它最初由光源發射之間經過的時間被稱為回溯時間。
宇宙學 - 角直徑距離
本章將瞭解角直徑距離是什麼以及它如何幫助宇宙學。
對於當前宇宙 −
$\Omega_{m,0} \: = \: 0.3$
$\Omega_{\wedge,0} \: = \: 0.69$
$\Omega_{rad,0} \: = \: 0.01$
$\Omega_{k,0} \: = \: 0$
到目前為止,我們已經學習了兩種型別的距離:
自行距離 (lp)——光子從光源傳播到我們的距離,即瞬時距離。
共動距離 (lc)——在不膨脹的空間中物體之間的距離,即在共動參考系中的距離。
距離作為紅移的函式
考慮一個星系,它在時間t1輻射光子,該光子在t0被觀察者探測到。我們可以將星系的自行距離寫為:
$$ l_p = \int_{t_1}^{t_0} cdt $$
設星系的紅移為z,
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\frac{1}{a}$$
$$\therefore \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$
現在,星系在任意時刻t的共動距離為:
$$l_c = \frac{l_p}{a(t)}$$
$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$
用z表示為:
$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$
有兩種方法可以求距離,如下:
通量-光度關係
$$F = \frac{L}{4\pi d^2}$$
其中d是光源的距離。
光源的角直徑距離
如果我們知道光源的大小,它的角寬度就可以告訴我們它與觀測者的距離。
$$\theta = \frac{D}{l}$$
其中l是光源的角直徑距離。
θ是光源的角大小。
D是光源的大小。
考慮一個大小為D,角大小為dθ的星系。
我們知道:
$$d\theta = \frac{D}{d_A}$$
$$\therefore D^2 = a(t)^2(r^2 d\theta^2) \quad \because dr^2 = 0; \: d\phi ^2 \approx 0$$
$$\Rightarrow D = a(t)rd\theta$$
將r改為rc,即星系的共動距離,我們有:
$$d\theta = \frac{D}{r_ca(t)}$$
這裡,如果我們選擇t = t0,我們將最終測量到星系的當前距離。但是D是在光子發射時測量的。因此,使用t = t0會得到星系距離更大的值,從而低估了它的尺寸。因此,我們應該使用時間t1。
$$\therefore d\theta = \frac{D}{r_ca(t_1)}$$
將此與之前的結果進行比較,我們得到:
$$d_\wedge = a(t_1)r_c$$
$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \because 1+z_1 = \frac{1}{a(t_1)}$$
因此,
$$d_\wedge = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$
dA是物體的角直徑距離。
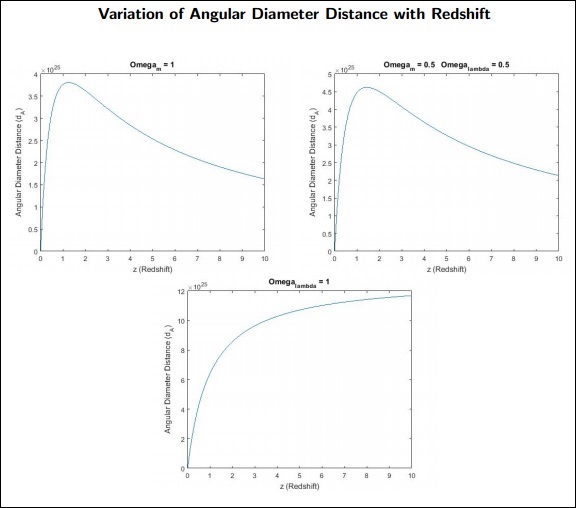
要點
如果我們知道光源的大小,它的角寬度就可以告訴我們它與觀測者的距離。
固有距離是光子從光源傳播到我們的距離。
共動距離是在不膨脹的空間中物體之間的距離。
宇宙學 - 光度距離
如前章所述,紅移為z的光源的角直徑距離由下式給出:
$$d_\wedge (z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
$$d_\wedge(z_{gal}) = \frac{r_c}{1+z_{gal}}$$
其中$r_c$是共動距離。
光度距離取決於宇宙學,它被定義為觀測到的通量f來自一個物體的距離。
如果已知遠處物體的固有光度$d_L$,我們可以透過測量通量$f$來計算其光度,該通量由下式確定:
$$d_L(z) = \sqrt{\frac{L}{4\pi f}}$$
光子能量發生紅移。
$$\frac{\lambda_{obs}}{\lambda_{emi}} = \frac{a_0}{a_e}$$
其中$\lambda_{obs}, \lambda_{emi}$分別是觀測波長和發射波長,$a_0, a_e$分別是相應的比例因子。
$$\frac{\Delta t_{obs}}{\Delta t_{emi}} = \frac{a_0}{a_e}$$
其中$\Delta_t{obs}$是觀測到的光子時間間隔,而$\Delta_t{emi}$是發射光子的時間間隔。
$$L_{emi} = \frac{nhv_{emi}}{\Delta t_{emi}}$$
$$L_{obs} = \frac{nhv_{obs}}{\Delta t_{obs}}$$
$\Delta t_{obs}$將比$\Delta t_{emi}$花費更多時間,因為探測器應該接收所有光子。
$$L_{obs} = L_{emi}\left ( \frac{a_0}{a_e} \right )^2$$
$$L_{obs} < L_{emi}$$
$$f_{obs} = \frac{L_{obs}}{4\pi d_L^2}$$
對於非膨脹宇宙,光度距離與共動距離相同。
$$d_L = r_c$$
$$\Rightarrow f_{obs} = \frac{L_{obs}}{4\pi r_c^2}$$
$$f_{obs} = \frac{L_{emi}}{4 \pi r_c^2}\left ( \frac{a_e}{a_0} \right )^2$$
$$\Rightarrow d_L = r_c\left ( \frac{a_0}{a_e} \right )$$
我們正在尋找光度距離$d_L$來計算發射物體$L_{emi}$的光度:
解釋:如果我們知道任何星系的紅移z,我們可以求出$d_A$,並由此計算出$r_c$。這用於求出$d_L$。
如果$d_L ! = r_c(a_0/a_e)$,那麼我們無法從$f_{obs}$中找到$L_{emi}$。
光度距離$d_L$和角直徑距離$d_A$之間的關係。
我們知道:
$$d_A(z_{gal}) = \frac{d_L}{1+z_{gal}}\left ( \frac{a_0}{a_e} \right )$$
$$d_L = (1 + z_{gal})d_A(z_{gal})\left ( \frac{a_0}{a_e} \right )$$
光子發射時的比例因子由下式給出:
$$a_e = \frac{1}{(1+z_{gal})}$$
當前宇宙的比例因子為:
$$a_0 = 1$$
$$d_L = (1 + z_{gal})^2d_\wedge(z_{gal})$$
選擇$d_L$還是$d_A$?
對於已知大小和紅移的星系,為了計算它有多大,使用$d_A$。
如果有一個給定視星等的星系,那麼要找出它有多大,就使用$d_L$。
示例:如果給定兩個紅移相等(z = 1)的星系,並且在天空平面中它們相隔2.3角秒,那麼這兩個星系之間的最大物理距離是多少?
為此,使用$d_A$如下:
$$d_A(z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
其中z = 1,根據星系的宇宙學引數替換H(z)。
要點
光度距離取決於宇宙學。
如果已知遠處物體的固有光度$d_L$,我們可以透過測量通量f來計算其光度。
對於非膨脹宇宙,光度距離與共動距離相同。
光度距離總是大於角直徑距離。
宇宙學 - Ia型超新星
對於任何給定的紅移 (z),我們有兩個距離值:
- 角直徑距離 (dA)
- 光度距離 (dL)
宇宙中沒有“宇宙學”距離的唯一定義。距離的選擇取決於應用的目的和方便性。
為了檢驗物體角大小隨紅移變化的預測趨勢,需要在天空使用標準尺寸的標尺。這應該是一個物體,它:
非常明亮,因此可以在 z > 1 時被探測到。
非常大,因此我們可以分辨其角大小。
在宇宙學上重要的時期內(z ∼ 1對應於大約7 Gyr 的回溯時間)沒有形態演化。
一些天體(如cD星系)滿足前兩個標準。但幾乎所有天體都被發現會隨著時間發生形態演化。一般來說,天體物理天體(延展光源)過去往往較小,因為它們仍在形成。
光度距離
光度距離取決於宇宙學。光度距離對宇宙學的依賴性使其成為宇宙學引數的有用度量。
如果我們能找到一個不會內在演化並且從區域性宇宙到高紅移宇宙都存在的標準燭光,那麼就可以估計宇宙學引數。
標準燭光是指其光度在不同光源之間沒有差異的光源。前提是標準燭光估計光度的任何差異都必須是由於宇宙學造成的。Ia型超新星就是這樣的一個燭光。
Ia型超新星 (SNe)
這些是白矮星在從其伴星(紅巨星或類似的主序星)吸積足夠質量後爆炸的結果,在一個雙星系統中。在紅巨星比白矮星的洛希瓣距離更近之後,質量轉移開始,最終白矮星爆炸產生巨大的能量,沒有留下核心。這些被稱為Ia型超新星。一個星系中Ia型超新星爆炸的典型速率是每世紀一次。
對Ia型超新星的搜尋一直在進行,不同的團隊參與其中:
- 高紅移超新星搜尋團隊(布萊恩·施密特、亞當·里斯等人)
- 超新星宇宙學專案(索爾·珀爾馬特等人)
還有一個名為卡內基超新星專案的研究團隊,他們給出了類似的結果。
不同團隊結果的相似性表明了Ia型超新星的宇宙學性質。因此,它們是有效的標準燭光。
要點
宇宙中沒有“宇宙學”距離的唯一定義。
角直徑距離和光度距離是最常用的。
標準燭光是指其光度在不同光源之間沒有差異的光源。
Ia型超新星滿足作為標準燭光的標準。
宇宙學 - 宇宙微波背景
CMB(宇宙微波背景)基本上是由物質和輻射處於平衡狀態時的光子構成的。到20世紀20年代,膨脹宇宙的思想已被接受,並可以回答一些問題。但關於較重元素的丰度和豐度的疑問仍未得到解答。此外,膨脹宇宙意味著物質的密度應該下降到0。
1948年,喬治·伽莫夫和拉爾夫·阿爾珀利用“大爆炸”解釋了較重元素的起源和豐度。他們與羅伯特·赫爾曼一起預測了“遺蹟輻射”的存在,即“大爆炸”後剩餘的輻射。這種殘餘輻射的預測溫度在50-6 K之間。1965年,羅伯特·迪克、吉姆·皮布林斯和戴維·威爾金森以及阿莫·佩裡齊亞斯研究小組透過實驗探測到了CMB。
早期的宇宙非常熱,能量太高,物質無法保持中性。因此,物質處於電離狀態——等離子體。輻射(光子)和物質(等離子體)主要透過以下三個過程相互作用。
康普頓散射——(主要相互作用過程)高能光子和低能帶電粒子之間的非彈性散射。
湯姆遜散射——光子被自由帶電粒子彈性散射。
逆康普頓散射——高能帶電粒子與低能光子。這些相互作用最終導致物質和輻射達到熱平衡。
熱平衡
在熱平衡中,輻射服從普朗克能量分佈,
$$B_v(T) = \frac{2hv^3}{c(e^{hv/k_BT}-1)}$$
在此期間,由於相互作用非常頻繁,光子的平均自由程非常小。宇宙對輻射是不透明的。早期宇宙是輻射主導的。宇宙以物質和輻射達到熱平衡並且它們的能量密度變得相等的方式演化。這可以從顯示密度隨比例因子變化的圖表中看出。讓我們找出物質和輻射達到平衡時的比例因子(時間)(a(t))。
$$\rho_m \propto \frac{1}{a^3}, \: \rho_r \propto \frac{1}{a^4}$$
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t)$$
在平衡時,
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = 1$$
$$\Rightarrow \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t) = 1 \: \Rightarrow a(t) = 2.96 \times 10^{-4}$$
使用$\Omega_{m,0} = 0.27$和$\Omega_{r,0} = 8 \times 10^{−5}$。對應於該比例因子的紅移由下式給出:
$$z = 1/a(t)-1 \approx 3375$$
由於宇宙膨脹,輻射能密度下降,從而宇宙開始冷卻。隨著光子能量的降低,中性原子開始形成。因此,在大約紅移1300左右,中性氫開始形成。這個時期的溫度接近3000K。
物質與輻射之間的相互作用變得非常不頻繁,因此宇宙開始變得對輻射透明。這段時期被稱為“最後散射面”,因為光子的平均自由程變得非常大,導致此後幾乎沒有發生散射。它也被稱為“宇宙光球”。
要點
CMB由物質和輻射處於平衡狀態時期的光子構成。
早期宇宙非常熱,能量太高,物質無法保持中性,因此它以電離物質——等離子體的形式存在。
康普頓散射、湯姆遜散射、逆康普頓散射是當時的三種物質-輻射相互作用過程。
宇宙演化使得物質和輻射達到熱平衡。
解耦時的CMB溫度
我們首先應該瞭解什麼特徵決定了解耦。我們知道能量高得多,以至於物質只以電離粒子的形式存在。因此,在解耦和複合時期,能量必須下降才能允許氫的電離。可以進行近似計算來估計解耦時的溫度。
計算過程如下:
首先,只考慮基態氫的電離。
$$hv \approx k_BT$$
$$\therefore T \approx \frac{hv}{k_B}$$
對於基態氫的電離,hν為13.6 eV,kB為玻爾茲曼常數8.61 × 10−5 eV/K,這表明溫度為1.5 × 105 開爾文。
這實質上告訴我們,如果溫度低於1.5 × 105 K,中性原子就可以開始形成。
我們知道光子與重子的比率約為5 × 1010。因此,即使在光子數量減少的圖表尾部,仍然會有足夠的光子來電離氫原子。此外,電子和質子的複合並不能保證基態氫原子。激發態需要較低的能量來電離。因此,應該針對具體情況進行嚴格的統計分析才能獲得準確的值。計算結果將溫度設定為約3000K。
為了解釋起見,我們考慮將氫激發到第一激發態的情況。能量大於ΔE的光子數Nγ (> ΔE)與光子總數Nγ的比率的一般表示式為:
$$\frac{N_\gamma(> \Delta E)}{N_\gamma} \propto e^{\frac{-\Delta E}{kT}}$$
對於將氫激發到第一激發態的情況,ΔE為10.2 eV。現在,如果我們考慮一個非常保守的數字,即每個重子至少有一個能量大於10.2 eV的光子(記住比率為5 × 1010),我們從公式3中得到溫度為4800 K(代入Nγ(> ΔE) = Np)。
這是產生第一激發態中性氫原子群的溫度。電離該態所需的溫度明顯較低。因此,我們得到了比1.5 × 105 K更好的估計值,更接近於公認值3000 K。
紅移-溫度關係
為了理解紅移和溫度之間的關係,我們採用以下兩種方法,如下所述。
方法1
從維恩位移定律,我們知道
$$\lambda_mT = 常數$$
為了將其與紅移聯絡起來,我們使用:
$$1+z = \frac{\lambda_0}{\lambda_e}$$
由於$λ_oT_o = λ_eT(z)$,我們得到:
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
將To設定為當前值3K,我們可以獲得給定紅移下的溫度值。
方法2
就頻率而言,我們知道:
$$v_0 = \frac{v_e}{1+z}$$
$$B_vdv = \frac{2hv^3}{c^2} \frac{dv}{e^{hv/kT}-1}$$
這告訴我們一定能量區間內光子的淨能量,hν是單個光子的能量。因此,我們可以透過Bνdν/hν獲得光子數。
如果$n_{νo}$代表現在,$n_{νe}$代表發射,我們得到:
$$\frac{n_{v_e}}{n_{v_0}} = (1+z)^3$$
簡化後,我們得到:
$$n_{v_0} =\frac{2v_c^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}\frac{1}{(1+z)^3}=\frac{2v_0^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}$$
這再次給出維恩位移定律,因此可以得出結論:
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
要點
- 早期宇宙非常熱,約為3000K。
- 目前的測量結果表明宇宙的溫度接近3K。
- 我們回溯的時間越遠,溫度就成比例地升高。
CMB輻射的各向異性與COBE衛星
本章將討論CMB輻射的各向異性和COBE(宇宙背景探測器)。
CMB中的主要各向異性
為了理解來自太空的觀測結果和宇宙微波背景輻射中的主要各向異性,讓我們考慮以下方程,並按如下所示理解它。
CMB光子數密度 (nγ,0)
$$n_{\gamma,0} = \frac{總能量密度}{光子的特徵能量}$$
$$n_{\gamma,0} = \frac{aT_0^4}{k_BT_0}$$
其中$k_B$是玻爾茲曼常數,$T_0$是宇宙目前的溫度。
使用目前的溫度$(T_0)$為2.7 K,我們得到當前的CMB光子數密度為400 cm−3。
在大的尺度上,宇宙恆星光子的數密度要小得多(≈10−3 cm−3)。
重子與光子的比率 (η)
如果來自星系的恆星貢獻(與CMB混合)可以忽略不計,則重子與質子的比率為:
$$\eta = \frac{n_{b,0}}{n_{\gamma,0}}$$
目前的值約為5 × 10−10。由於光子數密度和重子數密度都與a−3成正比,因此η不會隨時間變化。
能量密度
與數密度相反,目前物質能量密度比光子能量密度更占主導地位。
重子物質的能量密度 = $\rho_{b,0}c^2 = 0.04\rho_cc^2 = 2 × 10^{−9} ergcm^{−3}$。而輻射的能量密度 = $aT_0^4 = 4 \times 10^{−13}ergcm{−3}$。
CMB輻射的各向同性
彭齊亞斯和威爾遜發現,在觀測限度內,CMB是各向同性的。限度是儀器的低角解析度和靈敏度。他們在地球上進行觀測,因此無法透過所有光譜進行觀測,因為大氣中的水蒸氣吸收了從1mm到1m的許多波長。因此,CMB不能被認為是一個光譜。
CMB被認為是旋轉不變的(各向同性的)。由於存在物質和輻射處於平衡狀態的時期,因此宇宙中結構的形成是無法解釋的。由於物質的分佈不是各向同性的,而是像宇宙網一樣聚集在一起,中間有巨大的空洞,因此CMB被認為具有河外起源。
但是,隨著太空觀測的開始,發現了CMB中的各向異性,這導致人們推斷這些物質的各向異性導致了結構的形成。
從太空觀測CMB輻射
發射用於觀測CMB的主要衛星有:
宇宙微波背景探測器 (COBE, 1989)
威爾金森微波各向異性探測器 (WMAP, 2001) 和
普朗克 (2009).
COBE(宇宙背景探測器)
COBE主要有兩個儀器。它們是遠紅外絕對光譜儀(FIRAS)和差分微波輻射計(DMR天線)。FIRAS測量CMB的強度作為沿任何特定方向的波長的函式。而DMR有3個天線來測量來自三個不同方向的CMB強度的差異。以下要點為我們提供了有關FIRAS和DMR的更多資訊。
來自FIRAS的CMB觀測表明,CMB輻射對應於T = 2.72528±0.00065 K的黑體光譜。
DMR測量天空所有方向的三個頻率(31.5 GHz、53 GHz、90 GHz)。
DMR觀測中的“紅色蝙蝠俠符號”是來自前景發射(銀河系瀰漫同步輻射)的噪聲。
觀測中的強度變化對應於溫度變化。熱點和冷點的存在證明了CMB輻射是各向異性的。
這種各向異性一定存在於解耦時期,因為CMB沒有畸變。因此,物質應該有一些密度高於其他物質的區域。
COBE結果
CMB光譜(強度作為能量的函式)幾乎是完美的黑體,對應於T = 2.7 K。CMB輻射的比強度對於所有方向幾乎相同。證實了宇宙在大尺度上是各向同性的(驗證了我們對宇宙原理的假設)。
對資料的分析表明,在COBE(DMR)的解析度下,CMB光譜中存在溫度各向異性(“漲落”)。
COBE、WMAP、普朗克的解析度
COBE上的DMR儀器的極限(最大)空間解析度約為7度。
威爾金森微波各向異性探測器(WMAP)的平均解析度約為0.7度。
普朗克衛星的角解析度約為10角分。
要點
宇宙恆星光子的數密度遠小於CMB光子的數密度。
我們生活在一個物質主導的宇宙中,因為物質能量密度高於光子能量密度。
COBE、WMAP、普朗克都是為了測量和量化CMB中的各向異性而做出的努力。
宇宙中結構的形成是CMB各向異性的結果。
宇宙學——模擬CMB各向異性
當我們觀察精細校正的全天CMB圖時,會發現大量的 foreground contamination(前景汙染),這是一種地圖中的**各向異性**。我們可以看到這些前景輻射來自銀河系。CMB的強度沿銀道面較高,並隨著遠離銀道面而減弱。其中,我們可以觀測到二次各向異性,即來自星系的同步輻射。這些輻射構成了前景汙染。為了觀察來自天空的CMB輻射,我們需要減去這些前景輻射。
下圖顯示了帶有前景輻射的CMB。
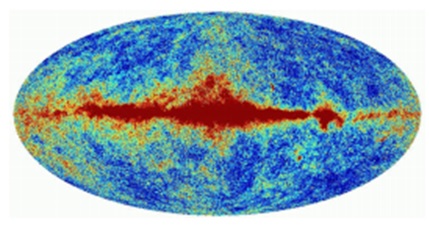
偶極各向異性
在CMB全天圖中還發現了另一種各向異性,稱為偶極各向異性。它與早期宇宙無關。這可以用球諧函式表示。如果球面上存在某種模式,並且我們想用數學函式對其進行對映,則可以使用三角函式。因此,當我們進行對映時,它可以是單極——各個方向都相同,或者偶極——旋轉180度時屬性發生反轉。類似地,我們還有四極等等。對於複雜的模式,它可以表示為這些單極、偶極、四極等的總和。
CMB模型認為,全天圖中各向異性的主要來源之一是這種偶極各向異性,但它並非CMB的原始模型。這可以在下面的影像中看到。
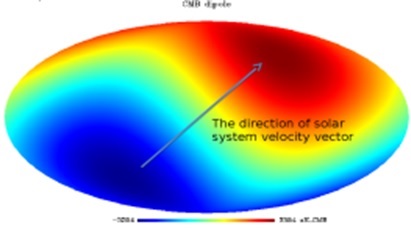
我們看到的偶極方向並非隨機方向。偶極各向異性具有方向性。我們沿著特定方向觀察CMB強度。這個方向是由太陽系速度向量決定的。地球的速度可以用相對於太陽或銀河系中心來表示。在地球運動的方向上,我們觀察到藍移和紅移,偶極位於此方向。
上圖具有典型的偶極外觀,因為我們的星系正在特定方向上運動。結果是——天空的一側看起來是紅移的,而天空的另一側看起來是藍移的。在這種情況下,紅移意味著光子的波長更長=更冷(所以與它們的名稱相反,它們在上圖中看起來是藍色的)。
我們可以說,地球相對於太陽/銀河系中心/天空中的CMB在給定時刻沿特定方向運動。然後,如果我們觀察任何角度並測量CMB的溫度,它都會有所不同。這是因為我們正在測量處於藍移或紅移狀態的光子,並且取決於天空中光子的視線。
要點
CMB全天圖中的前景汙染被稱為CMB的各向異性。
這些輻射來自我們自己的銀河系。
兩種各向異性是:偶極各向異性和角功率譜各向異性。
偶極各向異性在特定方向上,而角功率譜各向異性則遍佈各地。
最後散射面上的視界長度
視界長度是光子從“大爆炸”到“複合時期”所傳播的距離。角譜的第一個峰值位於θ = 1°(l = 180),這是一個非常特殊的長度尺度。
兩點之間的固有距離由下式給出:
$$r_p = \int_{0}^{t}cdt$$
當我們取時間範圍t = 0到t = trec時,則
$$r_H = \int_{0}^{t_{rec}}cdt$$
其中$r_H$是固有視界距離。
現在,我們知道:
$$\dot{a} = \frac{\mathrm{d} a}{\mathrm{d} t}$$
$$dt = \frac{da}{\dot{a}}$$
當t = 0時,a = 0。
則t = trec,a = a0 / (1 + zrec)。
因此,我們可以寫成:
$$r_H(z_{rec})=\int_{0}^{a_{rec}} c\frac{da}{aH}$$
$$H(a_{rec}) = H(z_{rec}) = H_0\sqrt{\Omega_{m,0}}a^{-3/2}$$
在**複合時期**,宇宙是物質主導的。即,**Ωrad << Ωmatter**。因此,輻射項被忽略。
$$r_H(z_{rec}) = \frac{c}{H_0\sqrt{\Omega_{m,0}}}\int_{0}^{a_{rec}} \frac{da}{a^{-1/2}}$$
$$r_H(z_{rec}) = \frac{2c}{3H_0\sqrt{\Omega_{m,0}}}\frac{1}{(1+z_{rec})^{3/2}}$$
$$\theta_H(rec) = \frac{r_H(z_{rec})}{d_A(z_{rec})}$$
如果我們將所有已知值代入方程,則等於0.5度。
從最後散射面來看,**電磁輻射**是不透明的。任何兩點如果不位於彼此的視界內,則不必具有相同的屬性。因此,它會給出不同的溫度值。
我們可以在此表面上找到兩點,它們彼此不相交,這意味著在某一點上宇宙膨脹速度超過光速,這就是膨脹的暴脹模型。
要點
視界長度是光子從“大爆炸”到“複合時期”所傳播的距離。
在複合時期,宇宙是物質主導的。
從最後散射面來看,電磁輻射是不透明的。
宇宙學 - 太陽系外行星探測
**天體生物學**是研究宇宙中生命起源、進化、分佈和未來的學科。它關注於發現和探測**太陽系外行星**。
**天體生物學**探討以下幾點:
生命如何開始和進化?(生物學 + 地質學 + 化學 + 大氣科學)
地球以外是否存在有利於生命存在的星球?(天文學)
地球生命的未來將會怎樣?
**天文學**探討以下幾點:
如何探測其他恆星周圍的行星系統?
其中一種方法是直接成像,但這項任務非常困難,因為與恆星相比,行星是極其微弱的光源,而且它們發出的微弱光線往往會淹沒在母恆星的光輝中。
當行星更靠近其母恆星且溫度較高時,對比度更好,因此它會發出強烈的紅外輻射。我們可以在紅外區域拍攝影像。
太陽系外行星探測技術
探測太陽系外行星最有效的方法如下。這些方法在後續章節中也將詳細解釋。
徑向速度法
它也稱為多普勒方法。在這個方法中:
恆星-行星系統繞它們的質心旋轉,恆星會擺動。
擺動可以透過以下方式檢測:
週期性的紅/藍移。天體測量——非常精確地測量天體的位置。
凌日法
凌星法(開普勒太空望遠鏡)用於確定大小。與雙星系統不同,行星導致恆星亮度下降通常非常小。
直接成像
使用望遠鏡對行星成像。
讓我們來看一個關於徑向速度法的案例研究。
案例研究
本案例研究的物件是圓形軌道,並且軌道的平面垂直於天空平面。兩者圍繞質心旋轉所需的時間相同。它等於兩次紅移或藍移之間的時間差。
請考慮下圖。
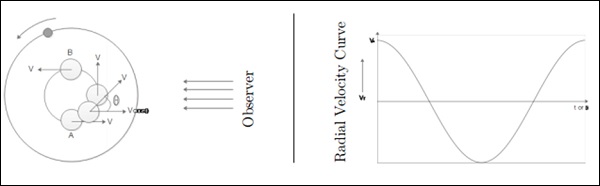
在A和C點——測量到全速度。在C點,速度為零。
Vrmax = V*是恆星的真實速度。
P是恆星和行星的週期。
θ是軌道的相位。
恆星質量 - M*,軌道半徑a*,行星質量**mp**。
根據質心方程:
$$m_p a_p = M_\ast a_\ast$$
根據速度方程:
$$V_\ast = \frac{2\pi a_\ast}{P}$$
$$\Rightarrow a_\ast = \frac{PV_\ast}{2\pi}$$
根據**開普勒定律**:
$$P^2 = \frac{4\pi^2a_p^3}{GM_\ast}$$
$$\Rightarrow a_p = \left ( \frac{P^2GM_\ast}{4\pi^2} \right)^{1/3}$$
根據上述方程,我們得到:
$$\Rightarrow m_p = \left( \frac{P}{2\pi G} \right)^{1/3}M_\ast^{2/3}V_\ast$$
我們得到:mp、ap和a*。
上述方程偏向於靠近恆星的大質量行星。
要點
天體生物學是研究宇宙中生命起源、進化、分佈和未來的學科。
探測太陽系外行星的技術包括:徑向速度法、凌星法、直接成像法等。
擺動可以透過週期性的紅/藍移和天體測量來檢測。
徑向速度法偏向於探測靠近恆星的大質量行星。
宇宙學 - 徑向速度法
在上一章中,討論了對於軌道平面和天空平面垂直的情況下的徑向速度法(針對圓形軌道)。在這裡,我們處理另一種情況,即軌道平面和天空平面不垂直的情況(針對圓形軌道)。
當軌道平面與天空平面成一定角度(不垂直)時,我們有以下情況:
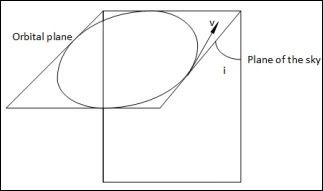
在這種情況下,當它們垂直時,我們有兩個點可以測量真實速度。但在這裡,這是不可能的。在所有點上,我們只能測量真實速度**v**的一個分量。
$$v_r = v \:sin(i)cos(\theta)$$
其中**θ**是軌道的相位,它是一個時間相關的量。另一方面,傾角**i**與時間無關。因此:
$$(v_r)_{max} = v\: sin(i)$$
觀測到的徑向速度曲線將具有以下形式:
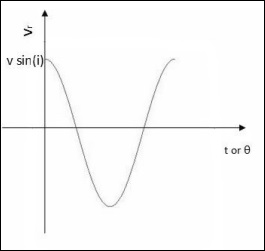
當軌道平面垂直於天空時:
$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$
其中**mp、P、G、M∗**分別代表行星質量、軌道週期、萬有引力常數和恆星質量。但在這種情況下,我們應該將其修改如下:
$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$
但是,找到i的值是一項困難的任務。我們可以使用凌星法對i的值施加某些約束。行星在恆星和地球之間經過稱為凌星。我們可以透過觀察凌星和光變曲線中觀測通量的顯著下降來獲得光變曲線,這意味著i接近90度。如果不滿足這些條件,我們就無法對i的值有任何瞭解。那麼我們找到的mp值可以作為行星質量的下限,因為它實際上是mp sin(i),而sin(i) ≤ 1。
總之,徑向速度法比凌星法更方便,因為徑向速度可以隨時測量,而凌星測量只能在凌星期間進行,而凌星持續時間可能不長。
要點
徑向速度法無法確定行星軌道的傾角。
徑向速度法優於凌星法,因為徑向速度可以始終測量,而凌星則不然。
凌星是短暫的,很容易錯過。
宇宙學 - 凌星法
凌星法**(開普勒太空望遠鏡)**用於確定大小。與雙星系統不同,行星導致恆星亮度下降通常非常小。
**F0**是行星掩食恆星之前恆星的通量。
**F1**是整個行星都在恆星前面後的通量。
下圖將用於所有計算。

$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$
$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$
$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$
$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$
地面望遠鏡難以做到這一點。這是透過哈勃望遠鏡實現的。

這裡,tT是A點和D點之間的時間,tF是B點和C點之間的時間。
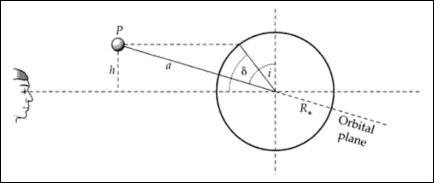
凌星的幾何形狀與系統的傾角**i**有關。凌星緯度和傾角可以互換。
根據上圖,我們可以寫成:
$$\frac{h}{a} = cos(i)$$
$$\frac{h}{R_\ast} = sin(\delta)$$
$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$
$$y^2 = (R_\ast + R_p)^2 - h^2$$
$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$
$$sin(\theta) = \frac{y}{a}$$
$$θ = arcsin\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$
$$t_T = \frac{P}{2\pi} \times 2θ$$
這裡,$t_T$ 是凌星發生所佔時間的比例,$(2θ/2π)$ 是凌星發生所佔角度的比例。
$$sin(\frac{t_Tπ}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$
通常情況下,a >> R∗ >> Rp。因此,我們可以寫成:
$$sin(\frac{t_Tπ}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$
這裡,P 是兩次連續凌星之間的時間間隔。凌星時間與軌道週期相比非常短。因此,
$$t_T = \frac{P}{π}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$
這裡,tT, P, R∗ 是可觀測量,a 和 i 需要求解。
現在,
$$sin(\frac{t_Fπ}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$
其中,$y^2 = (R_\ast − R_p)^2 − h^2$。
設,
$$\frac{ΔF}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$
現在,我們可以表示為:
$$\frac{a}{R_\ast} = \frac{2P}{π} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$
對於主序星,
$$R_\ast ∝ M^\alpha_\ast$$
$$\frac{R_\ast}{R_0} ∝ \left ( \frac{M_\ast}{M_0}\right )^\alpha$$
這給出R∗ 的值。
因此,我們也得到了 ‘a’ 的值。
所以,我們得到了 ‘Rp’,‘a’ 和 ‘i’。
對於所有這些,
$$h ≤ R_\ast + R_p$$
$$a\: cos\: i ≤ R_\ast + R_p$$
即使對於 i ≈ 89 度,凌星持續時間也非常短。行星必須非常靠近才能獲得足夠的凌星時間。這給 ‘i’ 提供了嚴格的約束。一旦我們得到 ‘i’,我們就可以從視向速度測量中推匯出 ‘mp’。
這種透過凌星法進行的探測被稱為偶然探測,即觀測到凌星的機率。凌星機率(觀測機率)的計算如下所示。
凌星機率與兩種極端凌星構型所描繪出的立體角有關,即:
$$行星立體角 = 2π \left ( \frac{2R_\ast}{a} \right )$$
以及在半長軸 a 處的總立體角,或:
$$球體立體角 = 4π$$
機率是這兩個面積的比率:
$$= \frac{有利方向所覆蓋的天區面積}{所有可能的軌道方向所覆蓋的天區面積}$$
$$= \frac{4π a_pR_\ast}{4π a^2_p} = \frac{R_\ast}{a_p} \quad \frac{空心圓柱體面積}{球體面積}$$
此機率與觀測者無關。
要點
- 凌星法(開普勒太空望遠鏡)用於確定大小。
- 凌星法探測是偶然探測。
- 行星必須非常靠近才能獲得足夠的凌星時間。
- 凌星機率與行星的立體角有關。
- 此機率與觀測者的參考系無關。
宇宙學 - 系外行星性質
2004年,首張系外行星的直接影像拍攝的是一顆質量為3-10 M木星的行星,它圍繞著一顆質量為25 M木星的褐矮星 (2M1207) 執行。視向速度法、凌星法、引力微透鏡法、成像法、天體測量法等技術已被用於探測系外行星。探測數量每年都在增加。
大約到2010年之前,視向速度法被廣泛使用,但現在大多數探測都是透過凌星法完成的。2014年探測數量激增,那是開普勒太空望遠鏡 (KST) 開始提供結果的時候。
質量-週期分佈表明,視向速度法更容易偏向於探測具有更大週期的巨型行星,而使用凌星法,只能探測到週期較短的行星,如下面的影像所示(資料來源:NASA 系外行星檔案)。

自從KST出現以來,較小質量行星的探測數量大幅增加。從下圖可以看出這一點。KST探測到的行星分為兩類:被稱為“熱木星”的熱巨行星和被稱為“熱超級地球”(因為它們的質量大於地球)的較小質量行星。
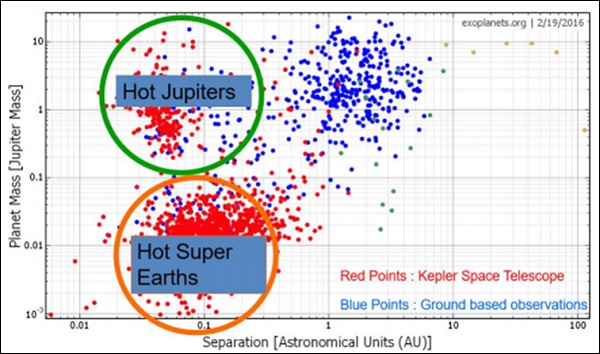
當我們繪製探測到的系外行星數量與它們到我們的距離的關係圖時,我們發現大多數這些行星都在2kpc以內,這遠在我們銀河系內。也許宇宙中行星並不罕見,因為我們的探測僅限於宇宙非常小的一部分中某種型別的行星。
行星是由星周盤或原行星盤形成的。如果行星是在恆星形成過程中產生的副產品,那麼宇宙中行星的數量可能超過宇宙中恆星的數量!!
宜居帶
宜居帶可以定義為恆星周圍水可以以液態形式存在的一個區域。考慮一顆距離恆星 $a_p$ 的行星,如下圖所示。計算行星溫度的一種簡單方法如下所示。
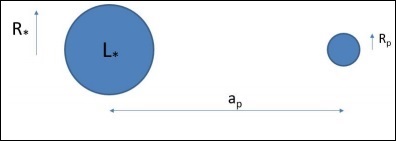
$$\left ( \frac{L_\ast}{4π a^2_p} \right )π R^2_p(1 - A) = 4π R^2_p σ T^4_p$$
以及
$$\frac{L_\ast}{4π R^2_\ast} = σ T^4_\ast$$
$$\therefore T_p = (1 - A)T_\ast \sqrt{\frac{R_\ast}{2a_p}}$$
在我們的例子中,代入
L太陽 = 3.83 x 1026
ap = 1.5 ∗ 1011 以及
A = 0.3
將得到 $T_{地球} = 255K$。實際計算非常複雜,包括雲物理學。我們太陽系中的宜居帶位於0.9 AU到1.7 AU之間。
由於氣壓降低,太陽的光度隨時間增加。它開始燃燒氫時,亮度要暗30%。這將導致宜居帶遠離太陽。由於地球位於宜居帶的內邊緣附近,也許有一天它會移出這個區域!
持續宜居帶
簡而言之,它被稱為CHZ,可以定義為在恆星整個主序星生命週期中液態水可以存在的區域。KST已經探測到許多確實位於宜居帶的系外行星。
生物特徵是任何物質——例如元素、同位素、分子或現象,它提供過去或現在生命的科學證據。一個例子是在一顆行星上同時探測到O2和CO2,這通常僅靠地質過程是無法實現的。這種探測是透過分析吸收光譜完成的。
要點
視向速度法、凌星法、引力微透鏡法、成像法、天體測量法等技術已被用於探測系外行星。
視向速度法更容易偏向於探測具有更大週期的巨型行星。
熱巨行星被稱為“熱木星”,較小質量行星被稱為“熱超級地球”。
宇宙中行星的數量超過宇宙中恆星的數量。
宜居帶可以定義為恆星周圍水可以以液態形式存在的一個區域。