灰度級解析度

---

---

影像解析度

解析度可以定義為影像中畫素的總數。這在影像解析度中已經討論過。我們還討論過，影像的清晰度並不取決於畫素的數量，而是取決於影像的空間解析度。這在空間解析度中已經討論過。在這裡，我們將討論另一種型別的解析度，稱為灰度級解析度。

灰度級解析度

灰度級解析度是指影像中陰影或灰度水平的可預測或確定性變化。

簡而言之，灰度級解析度等於每畫素的位元數。

我們已經在每畫素位元數和影像儲存需求的教程中討論了每畫素位元數。我們將在本文中簡要定義 bpp。

BPP

影像中不同顏色的數量取決於顏色深度或每畫素的位元數。

數學上

可以在灰度級解析度和每畫素位元數之間建立的數學關係可以表示為。

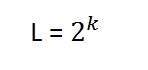
在這個等式中，L 指的是灰度級的數量。它也可以定義為灰度的陰影。而 k 指的是 bpp 或每畫素的位元數。因此，2 的每畫素位元數次冪等於灰度級解析度。

例如

上面愛因斯坦的影像是灰度影像。意味著它是一張每畫素 8 位或 8bpp 的影像。

現在如果要計算灰度級解析度，我們將這樣操作。

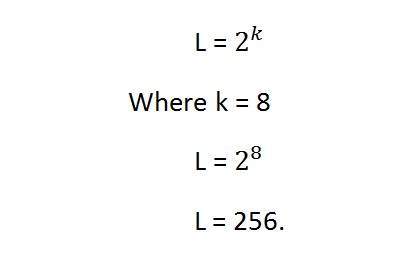
這意味著它的灰度級解析度為 256。或者換句話說，這張影像有 256 種不同的灰度陰影。

影像的每畫素位元數越高，其灰度級解析度越高。

根據 BPP 定義灰度級解析度

灰度級解析度不一定要僅根據級別來定義。我們也可以根據每畫素的位元數來定義它。

示例

如果您得到一張 4 bpp 的影像，並被要求計算其灰度級解析度。這個問題有兩個答案。

第一個答案是 16 個級別。

第二個答案是 4 位。

從灰度級解析度中查詢 bpp

您還可以從給定的灰度級解析度中找到每畫素的位元數。為此，我們只需要稍微修改一下公式。

公式 1。

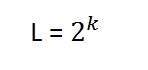
此公式查詢級別。現在如果我們要查詢每畫素的位元數，在本例中為 k，我們將簡單地將其更改為如下所示。

K = log 以 2 為底 (L) 公式 (2)

因為在第一個公式中，級別 (L) 和每畫素位元數 (k) 之間的關係是指數關係。現在我們必須將其反轉，因此指數的反函式是 log。

讓我們舉一個例子，從灰度級解析度中查詢每畫素的位元數。

例如

如果您得到一張 256 個級別的影像。它需要多少每畫素的位元數。

將 256 代入公式，我們得到。

K = log 以 2 為底 (256)

K = 8。

所以答案是每畫素 8 位。

灰度級解析度和量化

量化將在下一個教程中正式介紹，但在這裡我們只是要解釋灰度級解析度和量化之間的關係。

灰度級解析度在訊號的 y 軸上找到。在訊號與系統導論教程中，我們學習過對模擬訊號進行數字化需要兩個步驟。取樣和量化。

取樣在 x 軸上進行。量化在 Y 軸上進行。

因此，這意味著影像的灰度級解析度的數字化是在量化中完成的。