
- 數字影像處理
- 數字影像處理 - 首頁
- 數字影像處理 - 影像處理導論
- 數字影像處理 - 訊號與系統導論
- 數字影像處理 - 攝影史
- 數字影像處理 - 應用與用途
- 數字影像處理 - 維度的概念
- 數字影像處理 - 相機成像原理
- 數字影像處理 - 相機機制
- 數字影像處理 - 畫素的概念
- 數字影像處理 - 透視變換
- 數字影像處理 - 每畫素位元數的概念
- 數字影像處理 - 影像型別
- 數字影像處理 - 顏色程式碼轉換
- 數字影像處理 - 灰度圖到RGB轉換
- 數字影像處理 - 取樣的概念
- 數字影像處理 - 畫素解析度
- 數字影像處理 - 放大的概念
- 數字影像處理 - 放大方法
- 數字影像處理 - 空間解析度
- 數字影像處理 - 畫素、點和每英寸線條數
- 數字影像處理 - 灰度解析度
- 數字影像處理 - 量化的概念
- 數字影像處理 - ISO 感光度曲線
- 數字影像處理 - 抖動的概念
- 數字影像處理 - 直方圖導論
- 數字影像處理 - 亮度和對比度
- 數字影像處理 - 影像變換
- 數字影像處理 - 直方圖滑動
- 數字影像處理 - 直方圖拉伸
- 數字影像處理 - 機率論導論
- 數字影像處理 - 直方圖均衡化
- 數字影像處理 - 灰度變換
- 數字影像處理 - 卷積的概念
- 數字影像處理 - 掩碼的概念
- 數字影像處理 - 模糊的概念
- 數字影像處理 - 邊緣檢測的概念
- 數字影像處理 - Prewitt運算元
- 數字影像處理 - Sobel運算元
- 數字影像處理 - Robinson羅盤掩模
- 數字影像處理 - Krisch羅盤掩模
- 數字影像處理 - 拉普拉斯運算元
- 數字影像處理 - 頻域分析
- 數字影像處理 - 傅立葉級數和變換
- 數字影像處理 - 卷積定理
- 數字影像處理 - 高通濾波器與低通濾波器
- 數字影像處理 - 顏色空間導論
- 數字影像處理 - JPEG壓縮
- 數字影像處理 - 光學字元識別
- 數字影像處理 - 計算機視覺與圖形學
- 數字影像處理有用資源
- 數字影像處理快速指南
- 數字影像處理 - 有用資源
- 數字影像處理 - 討論
數字影像處理快速指南
數字影像處理導論
導論
訊號處理是電子工程和數學的一個學科,它處理模擬和數字訊號的分析和處理,並處理訊號的儲存、過濾和其他操作。這些訊號包括傳輸訊號、聲音或語音訊號、影像訊號以及其他訊號等等。
在所有這些訊號中,處理輸入為影像,輸出也為影像的訊號型別的領域稱為影像處理。顧名思義,它處理影像的處理。
它可以進一步細分為模擬影像處理和數字影像處理。
模擬影像處理
模擬影像處理是對模擬訊號進行的。它包括對二維模擬訊號的處理。在這種型別的處理中,影像透過改變電訊號的方式用電子方式進行處理。常見的例子包括電檢視像。
隨著時間的推移,數字影像處理由於其更廣泛的應用而佔據了模擬影像處理的主導地位。
數字影像處理
數字影像處理處理的是開發一個數字系統,該系統對數字影像執行操作。
什麼是影像
影像只不過是一個二維訊號。它由數學函式f(x,y)定義,其中x和y是水平和垂直的兩個座標。
f(x,y)在任何點的值都給出了影像該點的畫素值。

上圖是在計算機螢幕上看到的數字影像的示例。但實際上,這張影像只不過是0到255之間的一組二維數字陣列。
| 128 | 30 | 123 |
| 232 | 123 | 321 |
| 123 | 77 | 89 |
| 80 | 255 | 255 |
每個數字代表函式f(x,y)在任何點的值。在這種情況下,值128、230、123分別代表單個畫素值。圖片的尺寸實際上就是這個二維陣列的尺寸。
數字影像和訊號之間的關係
如果影像是一個二維陣列,那麼它與訊號有什麼關係呢?為了理解這一點,我們需要首先了解什麼是訊號?
訊號
在物理世界中,任何可以透過時間、空間或任何更高維度測量的量都可以被視為訊號。訊號是一個數學函式,它傳遞一些資訊。訊號可以是一維的、二維的或更高維度的。一維訊號是在時間上測量的訊號。常見的例子是語音訊號。二維訊號是在其他一些物理量上測量的訊號。二維訊號的例子是數字影像。我們將在下一個教程中更詳細地瞭解如何形成和解釋一維或二維訊號以及更高維的訊號。
關係
由於任何在物理世界中在兩個觀察者之間傳遞資訊或廣播訊息的東西都是訊號。這包括語音(人聲)或影像作為訊號。因為當我們說話時,我們的聲音被轉換成聲波/訊號,並根據我們說話的物件進行轉換。不僅如此,數字相機的工作方式也是如此,因為從數字相機獲取影像涉及將訊號從系統的一個部分傳輸到另一個部分。
數字影像是如何形成的
由於從相機捕捉影像是一個物理過程。陽光被用作能量來源。感測器陣列用於影像採集。因此,當陽光照射到物體上時,物體反射的光量由感測器感知,並且根據感知的資料生成連續的電壓訊號。為了建立數字影像,我們需要將此資料轉換為數字形式。這涉及取樣和量化。(稍後討論)。取樣和量化的結果是二維陣列或數字矩陣,它們就是數字影像。
重疊領域
機器/計算機視覺
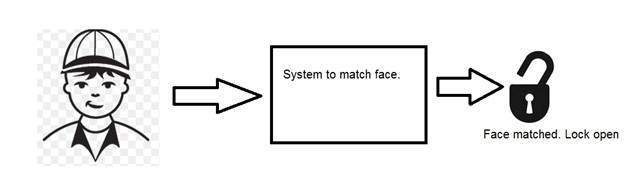
機器視覺或計算機視覺處理的是開發一個系統,其中輸入是影像,輸出是一些資訊。例如:開發一個掃描人臉並開啟任何型別鎖的系統。這個系統看起來像這樣。
計算機圖形學
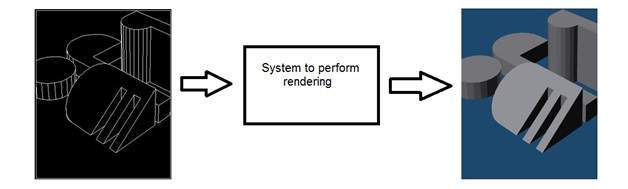
計算機圖形學處理的是從物件模型生成影像,而不是由某些裝置捕捉影像。例如:物件渲染。從物件模型生成影像。這樣的系統看起來像這樣。
人工智慧
人工智慧或多或少是將人類智慧融入機器的研究。人工智慧在影像處理中有很多應用。例如:開發計算機輔助診斷系統,幫助醫生解釋X射線、MRI等的影像,然後突出顯示醫生需要檢查的顯眼部分。
訊號處理
訊號處理是一個總稱,影像處理屬於它。物理世界(3D世界)中物體反射的光量透過相機的鏡頭,變成2D訊號,從而形成影像。然後使用訊號處理方法對該影像進行數字化,然後在數字影像處理中處理該數字影像。
訊號與系統導論
本教程涵蓋了理解數字影像處理概念所必需的訊號和系統的基礎知識。在深入探討具體概念之前,讓我們首先定義一些簡單的術語。
訊號
在電子工程中,表示某些資訊的根本量稱為訊號。資訊是什麼並不重要,即:模擬資訊還是數字資訊。在數學中,訊號是一個傳遞某些資訊的函式。事實上,任何可以透過時間、空間或任何更高維度測量的量都可以被視為訊號。訊號可以是任何維度,可以是任何形式。
模擬訊號
訊號可以是模擬量,這意味著它是相對於時間定義的。它是一個連續訊號。這些訊號在連續的獨立變數上定義。它們難以分析,因為它們攜帶大量的值。由於樣本值很大,它們非常精確。為了儲存這些訊號,需要無限的記憶體,因為它可以在實線上達到無限的值。模擬訊號用正弦波表示。
例如
人聲
人聲是模擬訊號的一個例子。當你說話時,產生的聲音以壓力波的形式透過空氣傳播,因此屬於一個數學函式,具有空間和時間的自變數以及對應於氣壓的值。
另一個例子是下圖所示的正弦波。
Y = sin(x),其中x是自變數

數字訊號
與模擬訊號相比,數字訊號更容易分析。它們是不連續訊號。它們是對模擬訊號的近似。
數字代表離散值,因此這意味著它們使用特定值來表示任何資訊。在數字訊號中,只使用兩個值來表示某些東西,即:1和0(二進位制值)。數字訊號不如模擬訊號精確,因為它們是在一段時間內獲取的模擬訊號的離散樣本。但是,數字訊號不受噪聲的影響。因此,它們持續時間長,易於解釋。數字訊號用方波表示。
例如
計算機鍵盤
每當按下鍵盤上的某個鍵時,就會向鍵盤控制器傳送相應的電訊號,其中包含該鍵的ASCII值。例如,按下鍵盤鍵a時生成的電訊號以0和1的形式攜帶數字97的資訊,這是字元a的ASCII值。
模擬訊號和數字訊號的區別
| 比較元素 | 模擬訊號 | 數字訊號 |
|---|---|---|
| 分析 | 困難 | 可分析 |
| 表示 | 連續的 | 非連續的 |
| 精度 | 更精確 | 不太精確 |
| 儲存 | 無限記憶體 | 易於儲存 |
| 受噪聲影響 | 是 | 否 |
| 記錄技術 | 原始訊號得以保留 | 對訊號進行取樣並保留 |
| 示例 | 人聲、溫度計、模擬電話等 | 計算機、數字電話、數字筆等 |
系統
系統由其處理的輸入和輸出型別定義。由於我們處理的是訊號,因此在我們的例子中,系統可以是數學模型、一段程式碼/軟體、物理裝置或黑盒,其輸入為訊號,對該訊號進行處理,輸出也是訊號。輸入稱為激勵,輸出稱為響應。

上圖顯示了一個系統,其輸入和輸出都是訊號,但輸入是模擬訊號,輸出是數字訊號。這意味著我們的系統實際上是一個將模擬訊號轉換為數字訊號的轉換系統。
讓我們來看看這個黑盒系統的內部
模擬訊號到數字訊號的轉換
由於模擬到數字轉換以及反向轉換涉及許多概念,我們將僅討論與數字影像處理相關的那些概念。轉換過程中涉及兩個主要概念。
取樣
量化
取樣
顧名思義,取樣可以定義為獲取樣本。沿x軸獲取數字訊號的樣本。取樣是在自變數上進行的。對於這個數學方程

取樣是在x變數上進行的。我們也可以說,x軸(無限值)到數字的轉換是在取樣下完成的。
取樣進一步分為上取樣和下采樣。如果x軸上的值範圍較小,我們將增加值的樣本數。這稱為上取樣,反之稱為下采樣。
量化
顧名思義,量化可以定義為劃分成量子(分割槽)。量化是在因變數上進行的。它與取樣相反。
對於這個數學方程 y = sin(x)
量化是在Y變數上進行的。它是在y軸上進行的。將y軸的無限值轉換為1、0、-1(或任何其他級別)稱為量化。
這是將模擬訊號轉換為數字訊號時涉及的兩個基本步驟。
下圖顯示了訊號的量化。

為什麼我們需要將模擬訊號轉換為數字訊號?
第一個也是最明顯的原因是,數字影像處理處理的是數字影像,即數字訊號。因此,無論何時捕獲影像,都將其轉換為數字格式,然後進行處理。
第二個也是重要的原因是,為了用數字計算機對模擬訊號進行運算,必須將模擬訊號儲存在計算機中。而要儲存模擬訊號,需要無限的記憶體來儲存它。由於這是不可能的,所以我們將訊號轉換為數字格式,然後將其儲存在數字計算機中,然後對其進行運算。
連續系統與離散系統
連續系統
輸入和輸出都是連續訊號或模擬訊號的系統稱為連續系統。

離散系統
輸入和輸出都是離散訊號或數字訊號的系統稱為數字系統。

攝影史
照相機的起源
照相機和攝影的歷史並不完全相同。照相機的概念遠早於攝影的概念。
暗箱
照相機的歷史起源於亞洲。照相機的原理首先由中國哲學家墨子提出。它被稱為暗箱。照相機就是從這個原理髮展而來的。
暗箱一詞來源於兩個不同的詞:Camera和Obscura。Camera的意思是房間或某種型別的暗室,Obscura的意思是黑暗的。
中國哲學家提出的這個概念包括一個裝置,可以將周圍環境的影像投影到牆上。然而,它並非由中國人制造。

暗箱的創造
中國人的概念由一位穆斯林科學家伊本·海賽姆(Abu Ali Al-Hassan Ibn al-Haitham,通常被稱為伊本·海賽姆)變成了現實。他製造了第一個暗箱。他的照相機遵循針孔相機的原理。他大約在1000年左右製造了這個裝置。
行動式相機
1685年,約翰·贊恩製造了第一臺行動式相機。在此裝置出現之前,相機的大小相當於一個房間,並不便攜。雖然愛爾蘭科學家羅伯特·博伊爾和羅伯特·胡克製造了一種可移動的相機,但該裝置仍然非常龐大,難以從一個地方搬到另一個地方。
攝影的起源
雖然暗箱是由一位穆斯林科學家在1000年製造的,但它第一次實際使用是在13世紀由英國哲學家羅傑·培根描述的。羅傑建議使用相機來觀察日食。
達芬奇
雖然在15世紀之前已經有了很大的改進,但萊昂納多·迪·塞爾·皮耶羅·達·芬奇所做的改進和發現是顯著的。達芬奇是一位偉大的藝術家、音樂家、解剖學家和軍事工程師。他被認為發明了許多東西。他最著名的畫作之一包括《蒙娜麗莎》的畫像。

達芬奇不僅按照針孔相機的原理製造了暗箱,還將其用作繪畫輔助工具。在他的作品《大西洋古抄本》中,定義了許多暗箱的原理。

他的相機遵循針孔相機的原理,可以描述為:
當被照射物體的影像穿過一個小孔進入一個非常黑暗的房間時,你會看到[在對面的牆上]這些物體以其正確的形狀和顏色,尺寸縮小,位置反轉,這是由於光線的交叉造成的。
第一張照片
第一張照片是由法國發明家約瑟夫·尼埃普斯於1814年拍攝的。他用瀝青塗抹錫板,然後曝光,從而捕捉到勒格拉斯窗戶外的第一張照片。

第一張水下照片
第一張水下照片是由英國數學家威廉·湯姆森使用防水箱拍攝的。這是在1856年完成的。

膠片的起源
膠片的起源是由美國發明家和慈善家喬治·伊士曼提出的,他被認為是攝影的先驅。
他創立了一家名為伊士曼柯達的公司,該公司以開發膠片而聞名。該公司於1885年開始生產紙質膠捲。他首先創造了柯達相機,然後是布朗尼相機。布朗尼是一款盒式相機,由於其快照功能而廣受歡迎。

膠捲出現後,相機行業再次蓬勃發展,一項發明又導致另一項發明。
徠卡和雅格
徠卡和雅格是分別於1925年和1939年開發的兩款模擬相機。徠卡相機使用35毫米電影膠片製造。

雅格是另一款使用35毫米格式的模擬相機,與徠卡相比,價格相對便宜,因此非常受歡迎。

模擬閉路電視攝像機
1942年,德國工程師瓦爾特·布魯赫開發並安裝了第一套模擬閉路電視攝像機系統。他還被認為在1960年發明了彩色電視。
Photo Pac
第一臺一次性相機於1949年由Photo Pac推出。這款相機只是一次性使用的相機,其中已經包含一卷膠捲。Photo pac的後續版本具有防水功能,甚至還配備了閃光燈。

數碼相機
索尼Mavica
索尼於1981年推出的Mavica(磁帶攝像機)是數碼相機領域的第一個改變遊戲規則的產品。影像記錄在軟盤上,稍後可以在任何顯示器上檢視。
它不是純數碼相機,而是一款模擬相機。但由於其將影像儲存在軟盤上的功能而廣受歡迎。這意味著現在可以長期儲存影像,並且可以在軟盤上儲存大量圖片,當軟盤滿了時,可以用新的空白軟盤替換。Mavica能夠在一張軟盤上儲存25張影像。
Mavica推出的另一個重要功能是其0.3兆畫素的拍照能力。

數碼相機
富士DS-1P相機由富士膠片於1988年推出,是第一款真正的數碼相機。
尼康D1是一款2.74兆畫素相機,是尼康開發的第一款商用數碼單反相機,專業人士也能輕鬆購買。

如今,數碼相機已內置於具有超高解析度和質量的手機中。
應用和用途
由於數字影像處理應用非常廣泛,幾乎所有技術領域都受到DIP的影響,我們只討論DIP的一些主要應用。
數字影像處理不僅僅侷限於調整相機拍攝的日常影像的空間解析度。它不僅僅侷限於提高照片的亮度等。它遠不止於此。
電磁波可以被認為是粒子流,其中每個粒子都以光速運動。每個粒子都包含一束能量。這束能量稱為光子。
根據光子的能量,電磁波譜如下所示。

在這個電磁波譜中,我們只能看到可見光譜。可見光譜主要包括七種不同的顏色,通常稱為(VIBGOYR)。VIBGOYR代表紫羅蘭色、靛藍色、藍色、綠色、橙色、黃色和紅色。
但這並不否定光譜中其他物質的存在。我們的肉眼只能看到可見部分,我們看到的所有物體都在其中。但相機可以看到肉眼看不到的其他東西。例如:X射線、伽馬射線等。因此,數字影像處理也對所有這些物質進行分析。
這種討論引出了另一個問題,即
為什麼我們還需要分析電磁波譜中的其他物質?
這個問題的答案在於,X射線等其他物質已廣泛應用於醫學領域。分析伽馬射線是必要的,因為它廣泛應用於核醫學和天文觀測。電磁波譜中的其他物質也是如此。
數字影像處理的應用
數字影像處理廣泛應用於的一些主要領域如下所示
影像銳化和復原
醫學領域
遙感
傳輸和編碼
機器/機器人視覺
色彩處理
模式識別
影片處理
顯微成像
其他
影像銳化和復原
影像銳化和復原在此指的是對現代相機拍攝的影像進行處理,使其變得更好,或者以某種方式操縱影像以達到預期效果的過程。它指的是Photoshop通常所做的工作。
這包括縮放、模糊、銳化、灰度到彩色轉換、邊緣檢測及其反向操作、影像檢索和影像識別。常見的例子有:
原始影像

縮放後的影像

模糊影像

銳化影像

邊緣

醫學領域
數字影像處理在醫學領域中的常見應用包括:
伽馬射線成像
PET掃描
X射線成像
醫學CT
紫外成像
紫外成像
在遙感領域,地球的區域由衛星或高地掃描,然後進行分析以獲取相關資訊。數字影像處理在遙感領域的一個特定應用是檢測地震造成的基礎設施損壞。
即使嚴重損壞集中在某些區域,要掌握這些損壞也需要較長時間。由於地震影響的區域有時非常廣闊,無法用肉眼檢查以評估損失。即使可以,也是一個非常繁瑣費時的過程。因此,數字影像處理提供了一種解決方案。從地面上方捕捉受影響區域的影像,然後對其進行分析以檢測地震造成的各種型別的損壞。

分析中的關鍵步驟包括:
邊緣提取
各種型別邊緣的分析和增強
傳輸和編碼
第一張透過電線傳輸的圖片是從倫敦透過海底電纜傳送到紐約的。傳送的圖片如下所示。

這張圖片從一個地方到另一個地方花了三個小時。
現在想象一下,今天我們能夠以幾秒鐘的延遲從一個大陸看到另一個大陸的即時影片或監控錄影。這意味著在這個領域也做了大量的工作。這個領域不僅關注傳輸,還關注編碼。許多不同的格式已經被開發出來,用於高頻寬或低頻寬的圖片編碼,然後透過網際網路等進行流傳輸。
機器/機器人視覺
除了機器人今天面臨的許多挑戰之外,最大的挑戰之一仍然是提高機器人的視覺能力。使機器人能夠看到物體、識別它們、識別障礙物等等。該領域做出了許多貢獻,並引入了另一個完整的計算機視覺領域來處理它。
障礙物檢測
障礙物檢測是透過影像處理完成的一項常見任務,它透過識別影像中的不同型別的物體,然後計算機器人與障礙物之間的距離。

循跡機器人
如今大多數機器人都是透過跟隨線路來工作的,因此被稱為循跡機器人。這幫助機器人沿著其路徑移動並執行某些任務。這也透過影像處理實現。

色彩處理
顏色處理包括彩色影像和使用的不同顏色空間的處理。例如RGB顏色模型、YCbCr、HSV。它還涉及研究這些彩色影像的傳輸、儲存和編碼。
模式識別
模式識別涉及影像處理和包括機器學習(人工智慧的一個分支)在內的各個其他領域的學習。在模式識別中,影像處理用於識別影像中的物體,然後使用機器學習來訓練系統以適應模式的變化。模式識別用於計算機輔助診斷、手寫識別、影像識別等。
影片處理
影片只不過是影像的快速運動。影片的質量取決於每分鐘的幀數/圖片數量以及所用每幀的質量。影片處理包括降噪、細節增強、運動檢測、幀速率轉換、縱橫比轉換、顏色空間轉換等。
維度的概念
我們將透過這個例子來理解維度的概念。
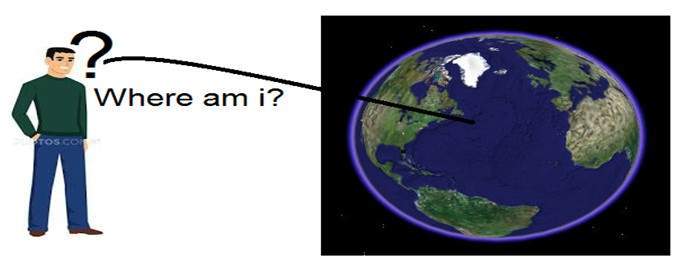
假設你有一個住在月球上的朋友,他想要在你生日那天送你禮物。他問你在地球上的住址。唯一的問題是月球上的快遞服務不理解字母地址,只理解數字座標。那麼你如何告訴他你在地球上的位置呢?
這就是維度的概念。維度定義了在空間中指出任何特定物體位置所需的最小點數。
讓我們回到之前的例子,你需要將你在地球上的位置傳送給住在月球上的朋友。你給他傳送三對座標。第一個稱為經度,第二個稱為緯度,第三個稱為高度。
這三個座標定義了你在地球上的位置。前兩個定義你的位置,第三個定義你高於海平面的高度。
這意味著只需要三個座標就能定義你在地球上的位置。這意味著你生活在一個三維世界中。這不僅回答了關於維度的問題,還回答了我們為什麼生活在三維世界中的原因。
由於我們是在參考數字影像處理來學習這個概念,所以我們現在將把這個維度的概念與影像聯絡起來。
影像的維度
如果我們生活在三維世界中,那麼我們捕捉到的影像的維度是什麼呢?影像是一個二維的,這就是我們也把影像定義為二維訊號的原因。影像只有高度和寬度。影像沒有深度。請看下面的影像。
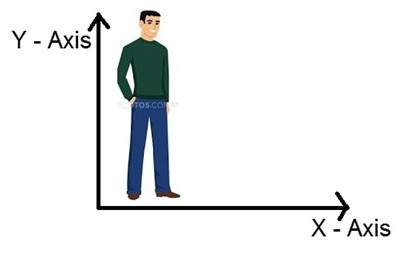
如果你觀察上面的圖形,它顯示它只有兩個軸,即高度軸和寬度軸。你無法從這張影像中感知深度。這就是我們說影像是一個二維訊號的原因。但是我們的眼睛能夠感知三維物體,但這將在下一節教程中更詳細地解釋相機是如何工作的以及影像是如何感知的。
這個討論引出了另一個問題,即如何從二維形成三維繫統。
電視是如何工作的?
如果我們觀察上面的影像,我們會看到它是一個二維影像。為了將其轉換為三維,我們需要另一個維度。讓我們以時間作為第三個維度,在這種情況下,我們將這個二維影像移動到第三個維度時間上。電視中發生的相同概念,這幫助我們感知螢幕上不同物體的深度。這是否意味著電視上顯示的內容或我們在電視螢幕上看到的內容是3D的?是的,我們可以這麼說。原因是,對於電視來說,如果我們播放影片,影片只不過是在時間維度上移動的二維影像。由於二維物體在第三個維度(時間)上移動,所以我們可以說它是三維的。
訊號的不同維度
一維訊號
一維訊號的常見例子是波形。它可以用數學表示為:
F(x) = 波形
其中x是自變數。因為它是一維訊號,所以只有一個變數x被使用。
一維訊號的圖示如下:
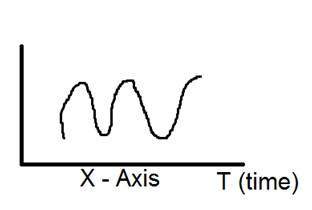
上圖顯示了一個一維訊號。
現在這又引出了另一個問題,那就是,即使它是一維訊號,為什麼它有兩個軸呢?這個問題的答案是,即使它是一維訊號,但我們是在二維空間中繪製它。或者我們可以說,我們表示這個訊號的空間是二維的。這就是為什麼它看起來像二維訊號。
也許你可以透過觀察下圖更好地理解一維的概念。

現在回到我們最初關於維度的討論,將上圖看作一條實線,從一點到另一點具有正數。現在,如果我們必須解釋這條線上任何點的位置,我們只需要一個數字,這意味著只有一個維度。
二維訊號
二維訊號的常見例子是影像,這已在上面討論過。
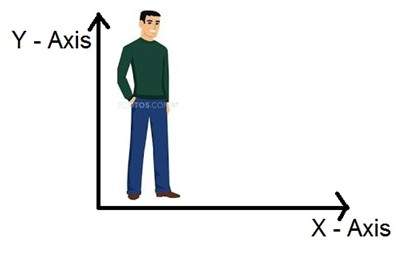
正如我們已經看到的那樣,影像是一個二維訊號,即它有兩個維度。它可以用數學表示為:
F(x, y) = 影像
其中x和y是兩個變數。二維的概念也可以用數學來解釋為:
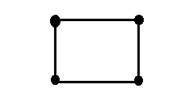
在上圖中,將正方形的四個角分別標記為A、B、C和D。如果我們稱圖中的一個線段為AB,另一個為CD,那麼我們可以看到這兩個平行線段連線起來構成一個正方形。每條線段對應一個維度,所以這兩條線段對應兩個維度。
三維訊號
顧名思義,三維訊號是指具有三個維度的訊號。開頭已經討論過最常見的例子,那就是我們的世界。我們生活在一個三維世界中。這個例子已經被非常詳細地討論過了。三維訊號的另一個例子是立方體或體資料,或者最常見的例子是動畫或3D卡通人物。
三維訊號的數學表示為:
F(x,y,z) = 動畫角色。
三維中包含另一個軸或維度Z,它給出了深度的錯覺。在笛卡爾座標系中,它可以被視為:
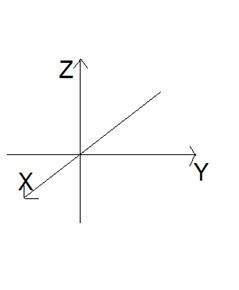
四維訊號
在四維訊號中,涉及四個維度。前三個與三維訊號相同:(X, Y, Z),新增的第四個是T(時間)。時間通常被稱為時間維度,它是一種衡量變化的方式。數學上,一個四維訊號可以表示為:
F(x,y,z,t) = 動畫電影。
四維訊號的常見例子可以是3D動畫電影。因為每個角色都是一個3D角色,然後它們隨著時間移動,因此我們看到了一個更像現實世界的三維電影的錯覺。
這意味著實際上動畫電影是四維的,即3D角色在第四維度時間上的移動。
相機成像
人眼是如何工作的?
在我們討論模擬和數字相機成像之前,我們必須首先討論人眼的成像。因為相機遵循的基本原理是從人眼的工作方式中借鑑的。
當光線照射到特定物體上時,它會在穿過物體後反射回來。光線透過眼睛晶狀體時,會形成一個特定角度,影像就會在視網膜(眼球后壁)上形成。形成的影像是倒立的。然後,這個影像會被大腦解讀,讓我們能夠理解事物。由於角度的形成,我們能夠感知到所看到物體的尺寸和深度。透視變換教程中對此進行了更詳細的解釋。
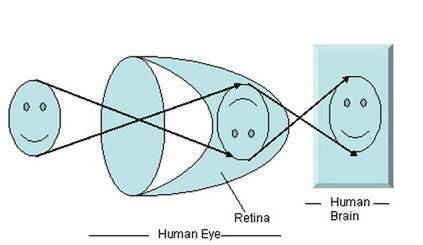
正如上圖所示,當陽光照射到物體上(在本例中,物體是一張臉)時,它會反射回來,不同的光線穿過晶狀體時會形成不同的角度,物體的倒立影像就會在後壁上形成。圖的最後部分表示該物體已被大腦解讀並重新正立。
現在讓我們回到模擬和數碼相機成像的討論。
模擬相機成像
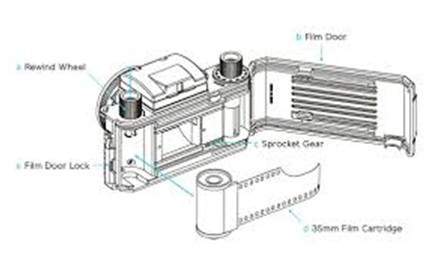
在模擬相機中,成像是由於用於成像的膠片上發生的化學反應。
模擬相機使用35毫米膠片。圖中用35毫米膠捲盒表示。這卷膠片塗有鹵化銀(一種化學物質)。

模擬相機使用35毫米膠片。圖中用35毫米膠捲盒表示。這卷膠片塗有鹵化銀(一種化學物質)。
光不過是由稱為光子的小粒子組成的。因此,當這些光子穿過相機時,它會與膠片上的鹵化銀粒子發生反應,從而產生影像的底片。
為了更好地理解它,讓我們看一下這個等式。
光子(光粒子)+ 鹵化銀 → 銀 → 底片

這只是基礎知識,雖然成像涉及許多其他關於光線內部透過的原理,以及快門和快門速度以及光圈及其開口的原理,但現在我們將繼續下一部分。雖然我們快門和光圈教程中已經討論了大多數這些概念。
這只是基礎知識,雖然成像涉及許多其他關於光線內部透過的原理,以及快門和快門速度以及光圈及其開口的原理,但現在我們將繼續下一部分。雖然我們快門和光圈教程中已經討論了大多數這些概念。
數碼相機成像
在數碼相機中,成像不是由於發生的化學反應,而是比這複雜一些。在數碼相機中,使用CCD感測器陣列進行成像。
透過CCD陣列成像

CCD代表電荷耦合器件。它是一種影像感測器,像其他感測器一樣,它感知數值並將它們轉換為電訊號。在CCD的情況下,它感知影像並將其轉換為電訊號等等。
這個CCD實際上是陣列或矩形網格的形狀。它就像一個矩陣,矩陣中的每個單元格都包含一個感測器,用於感知光子的強度。
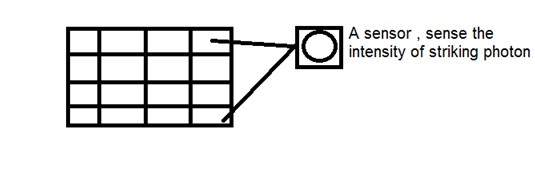
與模擬相機一樣,在數碼相機中,當光線照射到物體上時,光線會在撞擊物體後反射回來,並被允許進入相機內部。
CCD陣列的每個感測器本身都是一個模擬感測器。當光子照射到晶片上時,它會被儲存在每個光電感測器中作為一個小的電荷。每個感測器的響應直接等於照射在感測器表面的光量或(光子)能量。
由於我們已經將影像定義為二維訊號,並且由於CCD陣列的二維形成,可以從這個CCD陣列獲得完整的影像。
它具有有限數量的感測器,這意味著它可以捕捉的細節有限。此外,每個感測器針對照射在其上的每個光子粒子只能有一個值。
因此,光子撞擊(電流)的數量被計數和儲存。為了準確測量這些,外部CMOS感測器也與CCD陣列相連。
畫素簡介
CCD陣列中每個感測器的值指的是單個畫素的值。感測器數量 = 畫素數量。這也意味著每個感測器只能有一個值。
影像儲存
CCD陣列儲存的電荷一次一個畫素地轉換為電壓。在附加電路的幫助下,該電壓被轉換為數字資訊,然後被儲存。
每家生產數碼相機的公司都會製造自己的CCD感測器。其中包括索尼、三菱、尼康、三星、東芝、富士膠片、佳能等等。
除了其他因素外,拍攝影像的質量還取決於所使用的CCD陣列的型別和質量。
相機機制
在本教程中,我們將討論一些基本的相機概念,例如光圈、快門、快門速度、ISO,以及我們將討論這些概念的綜合使用以捕捉良好的影像。
光圈
光圈是一個小孔,允許光線進入相機內部。這是光圈的圖片。

你會看到光圈內部有一些像葉片一樣的東西。這些葉片形成一個可以開啟和關閉的八邊形形狀。因此,可以看出,葉片張開得越多,光線必須透過的孔就越大。孔越大,允許進入的光線就越多。
效果
光圈的效果直接對應於影像的亮度和暗度。如果光圈開得很大,它會允許更多光線進入相機。更多的光線會產生更多的光子,最終導致更亮的影像。
下面顯示了這個例子
考慮這兩張照片


右邊的照片看起來更亮,這意味著當它被相機捕捉時,光圈是完全開啟的。與左邊的那張照片相比,它比第一張照片暗得多,這表明當拍攝這張照片時,它的光圈沒有完全開啟。
尺寸
現在讓我們討論光圈背後的數學原理。光圈的大小用f值表示。它與光圈的開口成反比。
以下是兩個最能解釋這個概念的等式。
大光圈尺寸 = 小f值
小光圈尺寸 = 大f值
圖示可以表示為

快門
在光圈之後,就是快門。當光線允許透過光圈時,它會直接照射到快門上。快門實際上是一個蓋子,一個封閉的窗戶,或者可以認為是一個窗簾。記住當我們談論成像的CCD陣列感測器時。快門後面是感測器。因此,當光線透過光圈時,快門是成像和光線之間唯一的東西。
一旦快門開啟,光線就會照射到影像感測器上,影像就會在陣列上形成。
效果
如果快門允許光線透過更長的時間,影像會更亮。類似地,當快門移動得很快時,會產生更暗的圖片,因此允許透過的光線的光子很少,在CCD陣列感測器上形成的影像非常暗。
快門還有兩個主要概念
快門速度
快門時間
快門速度
快門速度可以指快門開啟或關閉的次數。請記住,我們不是在談論快門開啟或關閉多長時間。
快門時間
快門時間可以定義為
當快門開啟時,它關閉前等待的時間稱為快門時間。
在這種情況下,我們不討論快門開啟或關閉多少次,而是討論它開啟多長時間。
例如
我們可以透過這種方式更好地理解這兩個概念。假設快門開啟15次然後關閉,每次開啟1秒然後關閉。在這個例子中,15是快門速度,1秒是快門時間。
關係
快門速度和快門時間之間的關係是它們彼此成反比。
這種關係可以在下面的等式中定義。
快門速度越快 = 快門時間越短
快門速度越慢 = 快門時間越長。
解釋
所需時間越短,速度越快。所需時間越長,速度越慢。
應用
這兩個概念共同構成了各種應用。其中一些如下所示。
快速移動的物體
如果你要捕捉快速移動物體的影像,可能是汽車或任何東西。快門速度及其時間的調整會產生很大影響。
因此,為了捕捉這樣的影像,我們將進行兩次修改
提高快門速度
縮短快門時間
發生的情況是,當我們提高快門速度時,快門開啟或關閉的次數越多。這意味著不同的光線樣本會被允許透過。當我們縮短快門時間時,這意味著我們將立即捕捉場景並關閉快門。
如果你這樣做,你會得到一個快速移動物體的清晰影像。
為了理解這一點,我們將看看這個例子。假設你想捕捉快速移動的瀑布的影像。
你將快門速度設定為1秒,然後拍攝照片。這就是你得到的

然後你將快門速度設定為更快的速度,你得到。

然後再次將快門速度設定為更快,你得到。

你可以看到在最後一張圖片中,我們將快門速度提高到非常快,這意味著快門在1秒的200分之一內開啟或關閉,因此我們得到了一張清晰的影像。
ISO
ISO值用數字表示。它表示相機對光的靈敏度。如果ISO值降低,則表示我們的相機對光線不太敏感;如果ISO值較高,則表示它更敏感。
效果
ISO值越高,圖片越亮。如果ISO設定為1600,圖片會非常亮,反之亦然。
副作用
如果ISO增加,影像中的噪點也會增加。如今,大多數相機制造商都在努力在將ISO設定為更高速度時消除影像中的噪點。
畫素的概念
畫素
畫素是影像中最小的元素。每個畫素對應一個值。在8位灰度影像中,畫素值介於0到255之間。任何一點的畫素值對應於照射到該點的光子強度。每個畫素儲存一個與該特定位置的光強度成比例的值。
PEL
畫素也稱為PEL。你可以從下面給出的圖片中更好地理解畫素。
在上圖中,可能有數千個畫素共同構成這張影像。我們將放大影像,直到能夠看到一些畫素的劃分。它顯示在下面的影像中。

在上圖中,可能有數千個畫素共同構成這張影像。我們將放大影像,直到能夠看到一些畫素的劃分。它顯示在下面的影像中。
與CCD陣列的關係
我們已經看到了如何在CCD陣列中形成影像。因此,畫素也可以定義為
CCD陣列中最小的劃分也稱為畫素。
CCD陣列的每個劃分都包含針對照射到它的光子強度的值。這個值也可以稱為畫素。

總畫素數的計算
我們將影像定義為二維訊號或矩陣。在這種情況下,畫素 (PEL) 的數量等於行數乘以列數。
可以用下面的數學公式表示:
畫素總數 = 行數 (X) 列數
或者我們可以說,(x,y) 座標對的數量構成了畫素總數。
在影像型別教程中,我們將更詳細地講解如何在彩色影像中計算畫素。
灰度等級
任何一點的畫素值表示該位置影像的強度,這也稱為灰度等級。
在影像儲存和每畫素位數教程中,我們將更詳細地瞭解畫素值,但現在我們只關注單個畫素值的概念。
畫素值 (0)
正如本教程開頭已經定義的那樣,每個畫素只能有一個值,每個值表示影像該點的光強度。
現在讓我們來看一個非常獨特的值 0。值 0 表示沒有光。這意味著 0 表示黑色,進一步意味著當畫素值為 0 時,該點將形成黑色。
讓我們看看這個影像矩陣
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
現在這個影像矩陣全部填充為 0。所有畫素的值均為 0。如果我們要計算這個矩陣中的畫素總數,我們將這樣做:
畫素總數 = 行總數 X 列總數
= 3 X 3
= 9.
這意味著將生成一個包含 9 個畫素的影像,該影像的尺寸為 3 行 3 列,最重要的是該影像將是黑色的。
生成的影像將類似於:

為什麼這張影像是全黑的?因為影像中所有畫素的值都是 0。
透視變換
當人眼看近處物體時,它們看起來比遠處物體更大。這通常稱為透視。而變換是指將物體等從一種狀態轉換到另一種狀態。
因此,總的來說,透視變換處理的是將 3D 世界轉換為 2D 影像。這與人眼的視覺原理以及攝像機的原理相同。
我們將詳細解釋為什麼會發生這種情況,即靠近你的物體看起來更大,而遠離你的物體看起來更小,即使當你靠近它們時它們看起來更大。
我們將從參考系的概念開始討論。
參考系
參考系基本上是一組值,我們根據這些值來測量某些東西。
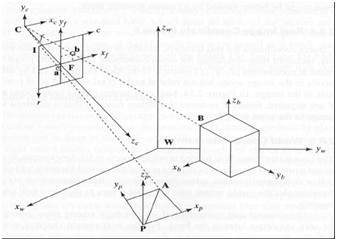
5 個參考系
為了分析 3D 世界/影像/場景,需要 5 個不同的參考系。
物體
世界
相機
影像
畫素
物體座標系
物體座標系用於對物體建模。例如,檢查特定物體相對於其他物體是否在正確的位置。它是一個 3D 座標系。
世界座標系
世界座標系用於關聯三維世界中的物體。它是一個 3D 座標系。
相機座標系
相機座標系用於根據相機的位置關聯物體。它是一個 3D 座標系。
影像座標系
它不是 3D 座標系,而是一個 2D 系統。它用於描述如何在 2D 影像平面上對映 3D 點。
畫素座標系
它也是一個 2D 座標系。每個畫素都有畫素座標值。
這五個座標系之間的變換

這就是 3D 場景如何轉換為包含畫素的 2D 影像。
現在我們將用數學方法解釋這個概念。
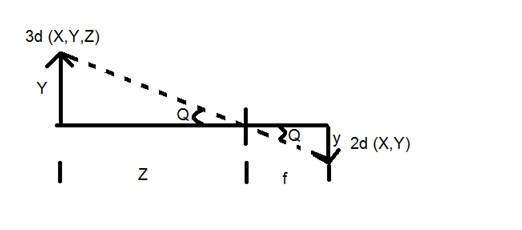 其中
其中Y = 3D 物體
y = 2D 影像
f = 相機的焦距
Z = 影像與相機之間的距離
在這個變換中形成了兩個不同的角度,用 Q 表示。
第一個角度是:
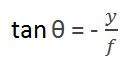
其中負號表示影像被反轉。形成的第二個角度是:
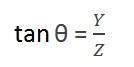
比較這兩個等式,我們得到:
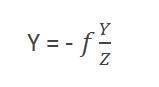
從這個等式中,我們可以看出,當光線從物體上反射回來後經過相機時,會形成一個倒立的影像。
我們可以透過這個例子更好地理解這一點。
例如
計算生成的影像大小
假設拍攝了一個身高 5 米的人的影像,該人距離相機 50 米,我們必須確定焦距為 50 毫米的相機拍攝的人的影像大小。
解答
由於焦距以毫米為單位,因此我們必須將所有單位轉換為毫米才能進行計算。
所以:
Y = 5000 毫米。
f = 50 毫米。
Z = 50000 毫米。
將這些值代入公式,我們得到:
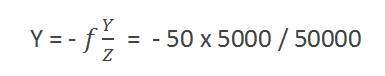
= -5 毫米。
同樣,負號表示影像被反轉。
每畫素位數的概念
Bpp 或每畫素位數表示每個畫素的位數。影像中不同顏色的數量取決於顏色深度或每畫素位數。
數學中的位
這就像玩二進位制位一樣。
一位可以表示多少個數?
0
1
可以組合出多少個兩位組合?
00
01
10
11
如果我們設計一個公式來計算可以從位中組合出的總數,它將是這樣的:
其中 bpp 表示每畫素位數。在公式中輸入 1,得到 2;輸入 2,得到 4。它呈指數增長。
不同顏色的數量
正如我們在開頭所說,不同顏色的數量取決於每畫素位數。
下表列出了一些位數及其對應的顏色。
| 每畫素位數 | 顏色數量 |
|---|---|
| 1 bpp | 2 種顏色 |
| 2 bpp | 4 種顏色 |
| 3 bpp | 8 種顏色 |
| 4 bpp | 16 種顏色 |
| 5 bpp | 32 種顏色 |
| 6 bpp | 64 種顏色 |
| 7 bpp | 128 種顏色 |
| 8 bpp | 256 種顏色 |
| 10 bpp | 1024 種顏色 |
| 16 bpp | 65536 種顏色 |
| 24 bpp | 16777216 種顏色(1670 萬種顏色) |
| 32 bpp | 4294967296 種顏色(42.94 億種顏色) |
此表顯示了不同的每畫素位數及其包含的顏色數量。
色階
你可以輕鬆注意到指數增長的模式。著名的灰度影像為 8 bpp,這意味著它包含 256 種不同的顏色或 256 個色階。
色階可以表示為:

彩色影像通常為 24 bpp 或 16 bpp 格式。
我們將在影像型別教程中詳細瞭解其他顏色格式和影像型別。
顏色值
我們之前在畫素概念教程中看到,0 畫素值表示黑色。黑色
記住,0 畫素值始終表示黑色。但是沒有固定值表示白色。白色
表示白色的值可以計算為:

對於 1 bpp,0 表示黑色,1 表示白色。
對於 8 bpp,0 表示黑色,255 表示白色。
灰色
計算出黑色和白色值後,就可以計算出灰色的畫素值。
灰色實際上是黑色和白色的中點。也就是說:
對於 8 bpp,表示灰色的畫素值為 127 或 128 bpp(如果從 1 開始計數,而不是從 0 開始)。
影像儲存要求
討論了每畫素位數之後,我們現在擁有計算影像大小所需的一切。
影像大小
影像的大小取決於三件事。
行數
列數
每畫素位數
計算大小的公式如下所示:
影像大小 = 行數 * 列數 * bpp
這意味著如果你有一張影像,比如說這張:

假設它有 1024 行和 1024 列。由於它是灰度影像,它有 256 個不同的灰色陰影,或者說每畫素位數為 8。將這些值代入公式,我們得到:
影像大小 = 行數 * 列數 * bpp
= 1024 * 1024 * 8
= 8388608 位。
但由於這不是我們識別的標準答案,因此我們將將其轉換為我們的格式。
轉換為位元組 = 8388608 / 8 = 1048576 位元組。
轉換為千位元組 = 1048576 / 1024 = 1024 KB。
轉換為兆位元組 = 1024 / 1024 = 1 MB。
這就是影像大小的計算和儲存方式。現在在公式中,如果給出影像的大小和每畫素位數,你還可以計算影像的行數和列數,前提是影像為正方形(行數和列數相同)。
影像型別
影像型別有很多,我們將詳細瞭解不同型別的影像及其顏色分佈。
二值影像
顧名思義,二值影像只包含兩個畫素值。
0 和 1。
在我們之前的每畫素位數教程中,我們已經詳細解釋了畫素值與其對應顏色的表示。
這裡 0 指的是黑色,1 指的是白色。它也稱為單色。
黑白影像
因此,生成的影像只包含黑色和白色,因此也可以稱為黑白影像。

沒有灰度等級
這張二值影像的一個有趣之處在於它沒有灰度等級。它只有兩種顏色:黑色和白色。
格式
二值影像的格式為PBM(行動式點陣圖)。
2、3、4、5、6位顏色格式
目前2、3、4、5和6位顏色格式的影像已不再廣泛使用。它們過去用於舊式電視顯示器或監控器顯示器。
但這些顏色格式每種都包含兩種以上的灰度等級,因此與二值影像不同,它們具有灰度。
2位有4種顏色,3位有8種顏色,4位有16種顏色,5位有32種顏色,6位有64種顏色。
8位顏色格式
8位顏色格式是最著名的影像格式之一。它包含256種不同的顏色陰影,通常稱為灰度影像。
8位顏色範圍從0到255。其中0代表黑色,255代表白色,127代表灰色。
此格式最初由早期版本的UNIX作業系統和早期彩色Macintosh電腦使用。
愛因斯坦的灰度影像如下所示

格式
這些影像的格式為PGM(行動式灰度圖)。
Windows系統預設不支援此格式。要檢視灰度影像,您需要使用影像檢視器或影像處理工具箱,例如Matlab。
灰度影像背後的原理
正如我們在之前的教程中多次解釋的那樣,影像不過是一個二維函式,可以用二維陣列或矩陣來表示。因此,對於上面顯示的愛因斯坦影像,其背後將是一個值範圍在0到255之間的二維矩陣。
但彩色影像並非如此。
16位顏色格式
這是一種彩色影像格式,包含65,536種不同的顏色,也稱為高色彩格式。
它已被微軟在其支援8位以上顏色格式的系統中使用。現在,這種16位格式和我們將要討論的下一個格式(24位格式)都是彩色格式。
彩色影像中的顏色分佈不像灰度影像那樣簡單。
16位格式實際上細分為三種格式:紅色、綠色和藍色,也就是著名的RGB格式。
下圖以圖示的方式表示。
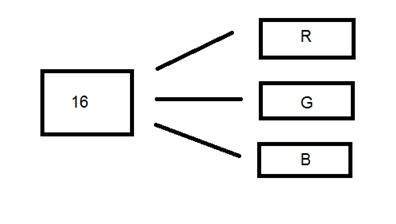
現在問題出現了,如何將16位分配給三種顏色?如果這樣做:
紅色5位,綠色5位,藍色5位
那麼最後會剩下1位。
因此,16位的分配方式如下:
紅色5位,綠色6位,藍色5位。
剩餘的1位被新增到綠色位中,因為在三種顏色中,綠色對眼睛最舒適。
請注意,並非所有系統都遵循這種分配方式。有些系統在16位中引入了alpha通道。
16位格式的另一種分配方式如下:
紅色4位,綠色4位,藍色4位,alpha通道4位。
或者有些系統這樣分配:
紅色5位,綠色5位,藍色5位,alpha通道1位。
24位顏色格式
24位顏色格式也稱為真彩色格式。與16位顏色格式一樣,在24位顏色格式中,24位再次分配給紅色、綠色和藍色的三種不同格式。
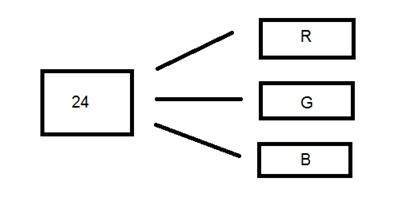
由於24可以被8整除,因此它被平均分配到三個不同的顏色通道。
它們的分配方式如下:
紅色8位,綠色8位,藍色8位。
24點陣圖像背後的原理
與只有一個矩陣的8位灰度影像不同,24點陣圖像有三個不同的矩陣:紅色、綠色和藍色。

格式
這是最常用的格式。其格式為PPM(行動式畫素圖),Linux作業系統支援該格式。著名的Windows系統有其自身的格式,即BMP(點陣圖)。
顏色程式碼轉換
在本教程中,我們將瞭解如何組合不同的顏色程式碼來建立其他顏色,以及如何將RGB顏色程式碼轉換為十六進位制程式碼,反之亦然。
不同的顏色程式碼
這裡的所有顏色都是24位格式,這意味著每種顏色都包含8位的紅色、8位的綠色和8位的藍色。或者我們可以說每種顏色都有三個不同的部分。您只需更改這三個部分的數量即可建立任何顏色。
二值顏色格式
顏色:黑色
影像

十進位制程式碼
(0,0,0)
解釋
正如在之前的教程中解釋的那樣,在8位格式中,0代表黑色。因此,如果要建立純黑色,則必須將R、G、B三個部分都設定為0。
顏色:白色
影像

十進位制程式碼
(255,255,255)
解釋
由於R、G、B的每個部分都是8位部分,所以在8位中,白色由255形成。這在畫素教程中有所解釋。因此,為了建立白色,我們將每個部分設定為255,這就是我們獲得白色的方式。透過將每個值設定為255,我們得到總值為255,這使顏色變為白色。
RGB顏色模型
顏色:紅色
影像

十進位制程式碼
(255,0,0)
解釋
由於我們只需要紅色,因此我們將綠色和藍色的其餘兩個部分清零,並將紅色部分設定為其最大值255。
顏色:綠色
影像

十進位制程式碼
(0,255,0)
解釋
由於我們只需要綠色,因此我們將紅色和藍色的其餘兩個部分清零,並將綠色部分設定為其最大值255。
顏色:藍色
影像

十進位制程式碼
(0,0,255)
解釋
由於我們只需要藍色,因此我們將紅色和綠色的其餘兩個部分清零,並將藍色部分設定為其最大值255。
灰色
顏色:灰色
影像

十進位制程式碼
(128,128,128)
解釋
正如我們在畫素教程中已經定義的那樣,灰色實際上是中點。在8位格式中,中點是128或127。在本例中,我們選擇128。因此,我們將每個部分設定為其中點128,這導致總中值,我們得到灰色。
CMYK顏色模型
CMYK是另一種顏色模型,其中c代表青色,m代表品紅色,y代表黃色,k代表黑色。CMYK模型通常用於彩色印表機,其中使用兩種顏色墨盒。一種包含CMY,另一種包含黑色。
CMY顏色也可以透過更改紅色、綠色和藍色的數量或部分來建立。
顏色:青色
影像

十進位制程式碼
(0,255,255)
解釋
青色是由綠色和藍色兩種不同顏色的組合形成的。因此,我們將這兩者設定為最大值,並將紅色的部分清零。然後我們得到青色。
顏色:品紅色
影像

十進位制程式碼
(255,0,255)
解釋
品紅色是由紅色和藍色兩種不同顏色的組合形成的。因此,我們將這兩者設定為最大值,並將綠色的部分清零。然後我們得到品紅色。
顏色:黃色
影像

十進位制程式碼
(255,255,0)
解釋
黃色是由紅色和綠色兩種不同顏色的組合形成的。因此,我們將這兩者設定為最大值,並將藍色的部分清零。然後我們得到黃色。
轉換
現在我們將瞭解顏色是如何從一種格式轉換為另一種格式的。
從RGB轉換為十六進位制程式碼
從十六進位制轉換為RGB的方法如下:
選擇一種顏色。例如:白色 = (255, 255, 255)。
取第一個部分,例如255。
將其除以16。如下所示:
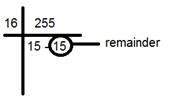
取下面兩行數字,即商和餘數。在本例中,它是15 ÷ 15,即FF。
對接下來的兩個部分重複步驟2。
將所有十六進位制程式碼組合成一個。
答案:#FFFFFF
從十六進位制轉換為RGB
從十六進位制程式碼轉換為RGB十進位制格式的方法如下:
取一個十六進位制數。例如:#FFFFFF
將其分成三部分:FF FF FF
取第一部分並將其元件分開:F F
分別將每個部分轉換為二進位制:(1111)(1111)
現在將各個二進位制數組合成一個:11111111
將此二進位制數轉換為十進位制:255
現在重複步驟2兩次。
第一步得到的值是R,第二步是G,第三步是B。
答案:(255,255,255)
下表列出了常見的顏色及其十六進位制程式碼。
| 顏色 | 十六進位制程式碼 |
|---|---|
| 黑色 | #000000 |
| 白色 | #FFFFFF |
| 灰色 | #808080 |
| 紅色 | #FF0000 |
| 綠色 | #00FF00 |
| 藍色 | #0000FF |
| 青色 | #00FFFF |
| 品紅色 | #FF00FF |
| 黃色 | #FFFF00 |
灰度到RGB轉換
我們在影像型別教程中已經定義了RGB顏色模型和灰度格式。現在我們將彩色影像轉換為灰度影像。轉換方法有兩種,各有優缺點。這兩種方法是:平均法
加權法或亮度法
平均法
平均法是最簡單的方法。您只需取三種顏色的平均值即可。由於它是RGB影像,因此這意味著您需要將r與g與b相加,然後除以3才能得到所需的灰度影像。
方法如下:
灰度 = (R + G + B) / 3
例如

如果您有一個如上所示的彩色影像,並且想要使用平均法將其轉換為灰度影像,則將出現以下結果。

解釋
有一點需要注意,原始作品會發生一些變化。這意味著我們的平均法有效。但結果並不理想。我們想將影像轉換為灰度影像,但這卻變成了一個相當黑的影像。
問題
這個問題的出現是由於我們取了三種顏色的平均值。由於三種不同的顏色具有三種不同的波長,並且對影像的形成有各自的貢獻,因此我們必須根據它們的貢獻來取平均值,而不是使用平均法進行平均。我們現在所做的是:
紅色33%,綠色33%,藍色33%
我們取每種顏色的33%,這意味著每個部分對影像的貢獻相同。但實際上並非如此。亮度法給出了這個問題的解決方案。
加權法或亮度法
您已經看到了平均法中出現的問題。加權法解決了這個問題。由於紅色在三種顏色中波長最長,綠色不僅波長比紅色短,而且綠色也是對眼睛最舒適的顏色。
這意味著我們必須減少紅色的貢獻,增加綠色的貢獻,並將藍色的貢獻放在這兩者之間。
因此,形成的新公式是
新的灰度影像 = ((0.3 * R) + (0.59 * G) + (0.11 * B))。
根據這個公式,紅色貢獻了30%,綠色貢獻了59%,在三種顏色中佔比最大,藍色貢獻了11%。
將此公式應用於影像,我們得到:
原始影像

灰度影像

解釋
正如你在這裡看到的,影像現在已經使用加權方法正確地轉換為灰度影像。與平均值方法的結果相比,這張影像更明亮。
取樣的概念
模擬訊號到數字訊號的轉換
大多數影像感測器的輸出是模擬訊號,我們無法對其進行數字處理,因為我們無法儲存它。我們無法儲存它,因為儲存一個可以具有無限值的訊號需要無限的記憶體。
因此,我們必須將模擬訊號轉換為數字訊號。
為了建立數字影像,我們需要將連續資料轉換為數字形式。這可以透過兩個步驟完成。
取樣
量化
我們現在將討論取樣,量化將在稍後討論,但現在我們將簡要討論這兩個步驟之間的區別以及這兩個步驟的必要性。
基本思想
將模擬訊號轉換為數字訊號的基本思想是:

將它的兩個座標軸 (x,y) 都轉換為數字格式。
由於影像不僅在其座標(x軸)上是連續的,而且在其幅度(y軸)上也是連續的,因此處理座標數字化的那部分稱為取樣。處理幅度數字化的那部分稱為量化。
取樣。
在我們的訊號與系統入門教程中已經介紹了取樣。但我們在這裡將更深入地討論。
這是我們討論的取樣內容。
取樣這個術語指的是獲取樣本
我們在取樣中對x軸進行數字化
它是在自變數上進行的
在方程式 y = sin(x) 中,它是在 x 變數上進行的
它進一步分為兩部分:上取樣和下采樣

如果你觀察上圖,你會看到訊號中有一些隨機變化。這些變化是由於噪聲造成的。在取樣中,我們透過採集樣本來減少這種噪聲。很明顯,我們採集的樣本越多,影像質量越好,噪聲去除得越多,反之亦然。
然而,如果你只對x軸進行取樣,訊號不會轉換為數字格式,除非你也對y軸進行取樣,這稱為量化。更多的樣本最終意味著你收集了更多的資料,在影像的情況下,這意味著更多的畫素。
與畫素的關係
由於畫素是影像中最小的元素。影像中的畫素總數可以計算為:
畫素 = 行總數 * 列總數。
假設我們共有25個畫素,這意味著我們有一個5 X 5的正方形影像。然後,正如我們在取樣中討論的那樣,更多的樣本最終會導致更多的畫素。這意味著我們對連續訊號的x軸進行了25次取樣。這指的是這張影像的25個畫素。
這導致了另一個結論,即由於畫素也是CCD陣列的最小劃分。所以這意味著它也與CCD陣列有關,可以解釋為:
與CCD陣列的關係
CCD陣列上的感測器數量直接等於畫素數量。由於我們已經得出畫素數量直接等於樣本數量的結論,這意味著樣本數量直接等於CCD陣列上的感測器數量。
過取樣。
我們一開始就定義了取樣進一步分為兩種型別。即上取樣和下采樣。上取樣也稱為過取樣。
過取樣在影像處理中有著非常廣泛的應用,即縮放。
縮放
我們將在接下來的教程中正式介紹縮放,但現在,我們只簡要解釋一下縮放。
縮放是指增加畫素數量,這樣當您縮放影像時,您將看到更多細節。
畫素數量的增加是透過過取樣完成的。縮放的一種方法,或增加樣本的方法,是透過鏡頭機械運動進行光學縮放,然後捕捉影像。但是我們必須在影像被捕捉後才能這樣做。
縮放和取樣之間存在差異。
概念相同,即增加樣本。但關鍵區別在於,取樣是在訊號上進行的,而縮放是在數字影像上進行的。
畫素解析度
在我們定義畫素解析度之前,有必要定義畫素。
畫素
我們已經在我們的畫素概念教程中定義了畫素,其中我們將畫素定義為影像的最小元素。我們還定義了畫素可以儲存與該特定位置的光強度成比例的值。
現在我們已經定義了畫素,我們將定義什麼是解析度。
解析度
解析度可以用多種方式定義。例如畫素解析度、空間解析度、時間解析度、光譜解析度。我們將討論畫素解析度。
你可能在自己的電腦設定中看到過,你的顯示器解析度是 800 x 600、640 x 480 等。
在畫素解析度中,解析度一詞指的是數字影像中畫素的總數。例如,如果一張影像有 M 行和 N 列,那麼它的解析度可以定義為 M X N。
如果我們將解析度定義為畫素總數,那麼畫素解析度可以用一組兩個數字來定義。第一個數字是圖片的寬度,或列上的畫素數,第二個數字是圖片的高度,或其寬度上的畫素數。
我們可以說,畫素解析度越高,影像質量越高。
我們可以將影像的畫素解析度定義為 4500 X 5500。
百萬畫素
我們可以使用畫素解析度計算相機的百萬畫素。
列畫素(寬度) X 行畫素(高度)/ 100萬。
影像的大小可以用其畫素解析度來定義。
大小 = 畫素解析度 X bpp(每畫素位數)
計算相機的百萬畫素
假設我們有一張尺寸為 2500 X 3192 的影像。
它的畫素解析度 = 2500 * 3192 = 7982350 位元組。
除以 100萬 = 7.9 = 8 百萬畫素(大約)。
縱橫比
另一個與畫素解析度相關的重要的概念是縱橫比。
縱橫比是影像寬度與影像高度的比率。它通常表示為兩個用冒號分隔的數字 (8:9)。這個比率在不同的影像和不同的螢幕上有所不同。常見的縱橫比有:
1.33:1、1.37:1、1.43:1、1.50:1、1.56:1、1.66:1、1.75:1、1.78:1、1.85:1、2.00:1 等
優點
縱橫比保持了影像在螢幕上外觀的平衡,這意味著它保持了水平和垂直畫素之間的比率。當縱橫比增加時,它不會使影像失真。
例如
這是一張示例影像,它有 100 行和 100 列。如果我們希望把它縮小,並且條件是質量保持不變,或者換句話說,影像不會失真,這就是它的實現方式。
原始影像

在 MS Paint 中保持縱橫比來更改行和列。
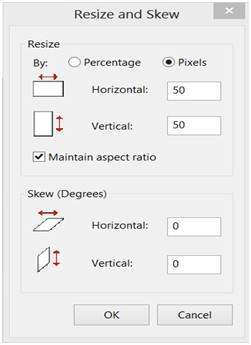
結果

較小的影像,但具有相同的平衡。
你可能在影片播放器中看到過縱橫比,你可以在其中根據你的螢幕解析度調整影片。
從縱橫比中查詢影像的尺寸
縱橫比告訴我們很多資訊。有了縱橫比,你就可以計算影像的尺寸以及影像的大小。
例如
如果給定一個縱橫比為 6:2、畫素解析度為 480000 畫素的灰度影像。
並且要求你計算兩件事。
分解畫素解析度以計算影像的尺寸
計算影像的大小
解答
已知
縱橫比:c:r = 6:2
畫素解析度:c * r = 480000
每畫素位數:灰度影像 = 8bpp
求
行數 = ?
列數 = ?
求解第一部分
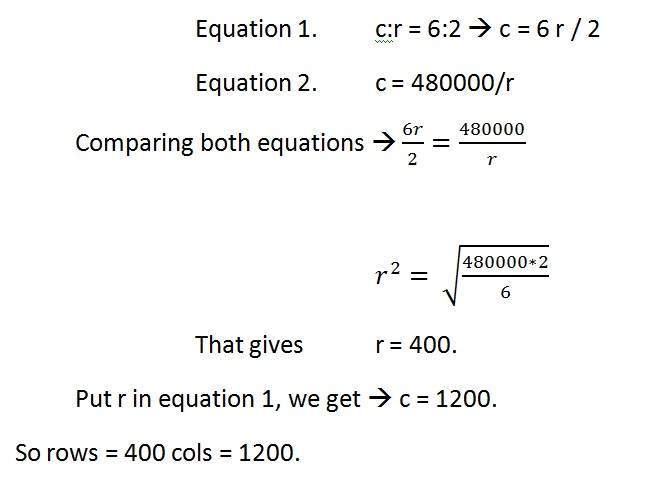
求解第二部分
大小 = 行數 * 列數 * bpp
影像大小(位)= 400 * 1200 * 8 = 3840000 位
影像大小(位元組)= 480000 位元組
影像大小(千位元組)= 48 KB(大約)。
縮放的概念
在本教程中,我們將介紹縮放的概念以及用於縮放影像的常用技術。
縮放
縮放簡單來說就是放大圖片,使影像中的細節變得更清晰可見。縮放影像有很多廣泛的應用,從透過相機鏡頭縮放,到在網際網路上縮放影像等等。
例如

被縮放

你可以分兩個步驟進行縮放。
第一步包括在拍攝特定影像之前進行縮放。這被稱為預處理縮放。這種縮放涉及硬體和機械運動。
第二步是在影像被捕捉後進行縮放。它是透過許多不同的演算法完成的,在這些演算法中,我們操縱畫素以放大所需的部分。
我們將在下一個教程中詳細討論它們。
光學變焦與數字變焦
這兩種型別的變焦都受相機的支援。
光學變焦
光學變焦是透過移動相機鏡頭來實現的。光學變焦實際上是真正的變焦。光學變焦的結果遠優於數字變焦。在光學變焦中,影像透過鏡頭放大,使得影像中的物體看起來更靠近相機。在光學變焦中,鏡頭會物理擴充套件以縮放或放大物體。
數字變焦
數碼變焦實際上是相機內部的影像處理過程。數碼變焦時,影像中心被放大,影像邊緣被裁切。由於中心被放大,看起來物體離你更近了。
數碼變焦時,畫素會被擴充套件,從而導致影像質量下降。
使用影像處理工具/軟體(例如Photoshop)透過電腦處理影像後,也能看到同樣的數碼變焦效果。
下圖是透過以下變焦方法中的一種實現數碼變焦的結果。

現在,由於我們正在學習數字影像處理,我們將不會關注如何使用鏡頭或其他工具進行光學影像變焦。相反,我們將重點關注能夠放大數字影像的方法。
變焦方法
雖然有很多方法可以做到這一點,但我們在這裡將討論其中最常用的幾種。
它們列在下面。
畫素複製或(最近鄰插值)
零階保持法
K倍變焦
這三種方法將在下一個教程中正式介紹。
變焦方法
在本教程中,我們將正式介紹在“變焦簡介”教程中介紹的三種變焦方法。
方法
畫素複製或(最近鄰插值)
零階保持法
K倍變焦
每種方法都有其自身的優缺點。我們將首先討論畫素複製。
方法一:畫素複製
導論
它也稱為最近鄰插值。顧名思義,在這種方法中,我們只是複製相鄰畫素。正如我們在取樣教程中已經討論過的那樣,變焦只不過是增加了樣本或畫素的數量。該演算法的工作原理相同。
工作原理
在這種方法中,我們根據已給定的畫素建立新的畫素。此方法中每個畫素在行和列方向上都複製n次,即可得到放大的影像。就這麼簡單。
例如
如果你有一個2行2列的影像,並且你想使用畫素複製將其放大兩倍或兩倍,這就是方法。
為了更好地理解,影像以矩陣的形式給出,其中包含影像的畫素值。
| 1 | 2 |
| 3 | 4 |
上圖有兩行兩列,我們首先將其按行放大。
按行放大
當我們按行放大時,我們只需簡單地將行的畫素複製到其相鄰的新單元格。
方法如下。
| 1 | 1 | 2 | 2 |
| 3 | 3 | 4 | 4 |
你可以看到,在上圖矩陣中,每個畫素在行中都被複制了兩次。
按列放大
下一步是按列複製每個畫素,我們將簡單地將列畫素複製到其相鄰的新列或其下方。
方法如下。
| 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 2 |
| 3 | 3 | 4 | 4 |
| 3 | 3 | 4 | 4 |
新影像大小
從上面的例子可以看出,一個原始影像為2行2列,放大後變成了4行4列。這意味著新影像的尺寸為
(原始影像行數 * 放大倍數,原始影像列數 * 放大倍數)
優點和缺點
這種變焦技術的優點之一是它非常簡單。你只需要複製畫素,無需其他操作。
這種技術的缺點是影像被放大,但輸出結果非常模糊。隨著放大倍數的增加,影像變得越來越模糊,最終會變成完全模糊的影像。
方法二:零階保持法
導論
零階保持法是另一種變焦方法。它也稱為兩倍變焦,因為它只能放大兩倍。我們將在下面的例子中看到原因。
工作原理
在零階保持法中,我們分別從行中選擇兩個相鄰元素,然後將它們相加,並將結果除以二,並將結果放在這兩個元素之間。我們首先按行進行此操作,然後按列進行此操作。
例如
讓我們取一個尺寸為2行2列的影像,並使用零階保持法將其放大兩倍。
| 1 | 2 |
| 3 | 4 |
我們首先按行放大,然後按列放大。
按行放大
| 1 | 1 | 2 |
| 3 | 3 | 4 |
我們取前兩個數字:(2 + 1) = 3,然後除以2,得到1.5,近似為1。第2行採用相同的方法。
按列放大
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 3 | 4 |
我們取兩個相鄰的列畫素值1和3。我們將它們相加得到4。然後將4除以2,得到2,將其放在它們之間。所有列都採用相同的方法。
新影像大小
你可以看到新影像的尺寸為3 x 3,而原始影像的尺寸為2 x 2。這意味著新影像的尺寸基於以下公式
(2(行數)- 1)X(2(列數)- 1)
優點和缺點。
這種變焦技術的優點之一是,它不會像最近鄰插值法那樣產生模糊的影像。但它也有一個缺點,即它只能作用於2的冪次方。這裡可以證明這一點。
兩倍變焦的原因
考慮上面2行2列的影像。如果我們必須使用零階保持法將其放大6倍,我們就無法做到。公式向我們展示了這一點。
它只能放大2的冪次方:2、4、8、16、32,依此類推。
即使你嘗試放大它,你也做不到。因為當你第一次將其放大兩倍時,結果將與按列放大時相同,尺寸為3x3。然後你再次放大它,你將得到尺寸為5 x 5的結果。現在如果你再次這樣做,你將得到尺寸為9 x 9的結果。
而根據你的公式,答案應該是11x11。(6(2) - 1)X(6(2) - 1)得到11 x 11。
方法三:K倍變焦
導論
K倍變焦是我們將要討論的第三種變焦方法。它是迄今為止討論的最完美的變焦演算法之一。它解決了雙倍變焦和畫素複製的挑戰。在這個變焦演算法中,K代表放大倍數。
工作原理
它的工作方式如下。
首先,你必須像在兩倍變焦中那樣取兩個相鄰畫素。然後你必須從較大的畫素中減去較小的畫素。我們稱此輸出為(OP)。
將輸出(OP)除以放大倍數(K)。現在你必須將結果新增到較小的值中,並將結果放在這兩個值之間。
再次將值OP新增到你剛剛放置的值中,並將其再次放置在上一個放置的值旁邊。你必須一直這樣做,直到放置k-1個值。
對所有行和列重複相同的步驟,你將得到一個放大的影像。
例如
假設你有一個2行3列的影像,如下所示。你必須將其放大三倍或三倍。
| 15 | 30 | 15 |
| 30 | 15 | 30 |
在這種情況下,K為3。K = 3。
應插入的值的數量為k-1 = 3-1 = 2。
按行放大
取前兩個相鄰畫素,它們是15和30。
從30中減去15。30-15 = 15。
將15除以k。15/k = 15/3 = 5。我們稱其為OP。(其中op只是一個名稱)
將OP新增到較小的數字中。15 + OP = 15 + 5 = 20。
再次將OP新增到20中。20 + OP = 20 + 5 = 25。
我們這樣做2次,因為我們必須插入k-1個值。
現在對接下來的兩個相鄰畫素重複此步驟。它顯示在第一個表中。
插入值後,你必須按升序對插入的值進行排序,以便它們之間保持對稱性。
它顯示在第二個表中
表1。
| 15 | 20 | 25 | 30 | 20 | 25 | 15 |
| 30 | 20 | 25 | 15 | 20 | 25 | 30 |
表2。

按列放大
必須按列執行相同的過程。該過程包括取兩個相鄰畫素值,然後從較大的值中減去較小的值。然後,你必須將其除以k。將結果儲存為OP。將OP新增到較小的值中,然後再次將OP新增到第一次新增OP的值中。插入新值。
經過所有這些操作後,你得到了什麼。
| 15 | 20 | 25 | 30 | 25 | 20 | 15 |
| 20 | 21 | 21 | 25 | 21 | 21 | 20 |
| 25 | 22 | 22 | 20 | 22 | 22 | 25 |
| 30 | 25 | 20 | 15 | 20 | 25 | 30 |
新影像大小
計算新影像尺寸的最佳方法是比較原始影像和最終影像的尺寸。原始影像的尺寸為2 X 3。新影像的尺寸為4 x 7。
因此,公式為
(K(行數- 1)+ 1)X(K(列數- 1)+ 1)
優點和缺點
K倍變焦演算法的一個明顯的優點是它能夠計算任何倍數的縮放,這是畫素複製演算法的優勢,它也提供了改進的結果(更清晰),這是零階保持法的優勢。因此,它結合了這兩種演算法的優勢。
這種演算法唯一的困難在於它最終必須進行排序,這是一個額外的步驟,因此增加了計算成本。
空間解析度
影像解析度
影像解析度可以用多種方式定義。其中一種是畫素解析度,這在畫素解析度和縱橫比的教程中已經討論過。
在本教程中,我們將定義另一種型別的解析度,即空間解析度。
空間解析度
空間解析度指出,影像的清晰度不能僅由畫素解析度決定。影像中的畫素數量並不重要。
空間解析度可以定義為
影像中最小的可辨細節。(數字影像處理 - Gonzalez,Woods - 第二版)
或者我們可以將空間解析度定義為每英寸的獨立畫素值數量。
簡而言之,空間解析度指的是我們不能比較兩種不同型別的影像來判斷哪一個清晰或哪一個不清晰。如果我們必須比較兩張影像以檢視哪一張更清晰或哪一張具有更高的空間解析度,我們必須比較兩張相同大小的影像。
例如
你不能比較這兩張影像來檢視影像的清晰度。


雖然兩張圖片都是同一個人,但這並非我們判斷的條件。左側圖片是愛因斯坦的縮圖,尺寸為 227 x 222 畫素。而右側圖片尺寸為 980 x 749 畫素,並且是放大的影像。我們無法比較這兩張圖片哪一張更清晰。請記住,縮放比例在此條件下並不重要,唯一重要的是這兩張圖片並不相同。
因此,為了測量空間解析度,下面的圖片可以達到目的。


現在您可以比較這兩張圖片了。兩張圖片的尺寸相同,均為 227 x 222 畫素。比較後,您會發現左側圖片的空間解析度更高,或者說比右側圖片更清晰。這是因為右側圖片是一張模糊的影像。
測量空間解析度
由於空間解析度指的是清晰度,因此對於不同的裝置,已經制定了不同的測量方法。
例如
每英寸點數 (Dots Per Inch)
每英寸線數 (Lines Per Inch)
每英寸畫素數 (Pixels Per Inch)
這些將在下一個教程中詳細討論,這裡僅作簡要介紹。
每英寸點數 (Dots Per Inch)
每英寸點數 (DPI) 通常用於顯示器。
每英寸線數 (Lines Per Inch)
每英寸線數 (LPI) 通常用於雷射印表機。
每英寸畫素數
每英寸畫素數 (PPI) 是用於平板電腦、手機等不同裝置的測量單位。
每英寸畫素、點數和線數
在上一個關於空間解析度的教程中,我們簡要介紹了 PPI、DPI 和 LPI。現在我們將正式討論它們。
每英寸畫素數。
畫素密度或每英寸畫素數是用於包括平板電腦和手機在內的不同裝置的空間解析度的衡量標準。
PPI 越高,質量越高。為了更好地理解它是如何計算的,讓我們計算一下一部手機的 PPI。
計算三星 Galaxy S4 的每英寸畫素數 (PPI)

三星 Galaxy S4 的 PPI 或畫素密度為 441。但它是如何計算的呢?
首先,我們將使用勾股定理來計算畫素中的對角線解析度。
它可以表示為
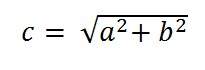
其中 a 和 b 是以畫素為單位的高度和寬度解析度,c 是以畫素為單位的對角線解析度。
對於三星 Galaxy S4,其解析度為 1080 x 1920 畫素。
因此,將這些值代入方程得到結果
C = 2202.90717
現在我們將計算 PPI
PPI = c / 以英寸為單位的對角線尺寸
三星 Galaxy S4 的對角線尺寸為 5.0 英寸,這可以在任何地方得到確認。
PPI = 2202.90717 / 5.0
PPI = 440.58
PPI ≈ 441
這意味著三星 Galaxy S4 的畫素密度為 441 PPI。
每英寸點數。
DPI 通常與 PPI 相關,但兩者之間存在差異。DPI 或每英寸點數是印表機空間解析度的衡量標準。對於印表機而言,DPI 表示在印表機列印影像時,每英寸列印多少墨點。
請記住,並非每個畫素都由一個墨點列印。列印一個畫素可能需要多個墨點。其原因是大多數彩色印表機使用 CMYK 模型。顏色是有限的。印表機必須從這些顏色中選擇來構成畫素的顏色,而在電腦中,您擁有成千上萬種顏色。
印表機的 DPI 越高,列印到紙張上的文件或影像的質量越高。
通常,一些雷射印表機的 DPI 為 300,而有些則為 600 或更高。
每英寸線數。
當 DPI 指的是每英寸點數時,每英寸線數指的是每英寸的點線數。半色調網點的解析度以每英寸線數來衡量。
下表顯示了一些印表機的每英寸線數容量。
| 印表機 | LPI |
|---|---|
| 絲網印刷 | 45-65 lpi |
| 雷射印表機 (300 dpi) | 65 lpi |
| 雷射印表機 (600 dpi) | 85-105 lpi |
| 膠印機 (新聞紙) | 85 lpi |
| 膠印機 (銅版紙) | 85-185 lpi |
灰度解析度
影像解析度
解析度可以定義為影像中畫素的總數。這在影像解析度中已經討論過。我們還討論過,影像的清晰度並不取決於畫素的數量,而是取決於影像的空間解析度。這在空間解析度中已經討論過。在這裡,我們將討論另一種型別的解析度,稱為灰度解析度。灰度解析度
灰度解析度指的是影像中陰影或灰度等級的可預測或確定性變化。
簡而言之,灰度解析度等於每畫素位數。
我們已經在每畫素位數和影像儲存需求教程中討論過每畫素位數。我們將在此處簡要定義 BPP。
BPP
影像中不同顏色的數量取決於顏色深度或每畫素位數。
數學上
灰度解析度和每畫素位數之間可以建立的數學關係可以表示為。
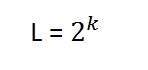
在這個等式中,L 指的是灰度級數。它也可以定義為灰度陰影。而 k 指的是 BPP 或每畫素位數。因此,2 的每畫素位數次方等於灰度解析度。
例如

上面愛因斯坦的圖片是灰度影像。這意味著它是一張每畫素 8 位或 8bpp 的影像。
現在如果要計算灰度解析度,我們將這樣計算。
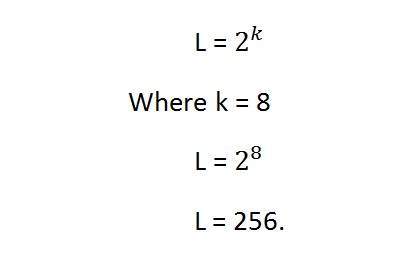
這意味著它的灰度解析度是 256。或者換句話說,這張圖片有 256 種不同的灰度陰影。
影像的每畫素位數越多,其灰度解析度越高。
根據 BPP 定義灰度解析度
灰度解析度不必僅以灰度級來定義。我們也可以用每畫素位數來定義它。
例如
如果給您一張 4 bpp 的影像,並要求您計算其灰度解析度。這個問題有兩個答案。
第一個答案是 16 個級別。
第二個答案是 4 位。
從灰度解析度中查詢 BPP
您也可以從給定的灰度解析度中找到每畫素位數。為此,我們只需要稍微修改一下公式。
公式 1。
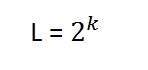
這個公式用於查詢級別數。現在如果我們要查詢每畫素位數,也就是 k,我們將簡單地將其更改為:
K = log₂(L) 公式 (2)
因為在第一個公式中,級別 (L) 和每畫素位數 (k) 之間的關係是指數關係。現在我們必須將其反轉,因此指數的反轉是 log。
讓我們舉個例子,從灰度解析度中找到每畫素位數。
例如
如果給您一張 256 個級別的影像。所需的每畫素位數是多少?
將 256 代入方程,我們得到:
K = log₂(256)
K = 8。
所以答案是每畫素 8 位。
灰度解析度和量化
量化將在下一個教程中正式介紹,但這裡我們只解釋灰度解析度和量化之間的關係。
灰度解析度位於訊號的 y 軸上。在訊號與系統導論教程中,我們學習到將模擬訊號數字化需要兩個步驟:取樣和量化。

取樣在 x 軸上進行。量化在 y 軸上進行。
這意味著影像灰度解析度的數字化是在量化中完成的。
量化概念
我們在訊號與系統教程中介紹了量化。我們將在此教程中正式將其與數字影像聯絡起來。讓我們先稍微討論一下量化。
訊號數字化。
正如我們在之前的教程中看到的,將模擬訊號數字化為數字訊號需要兩個基本步驟:取樣和量化。取樣在 x 軸上進行。它是將 x 軸(無限值)轉換為數字值的過程。
下圖顯示了訊號取樣。

與數字影像相關的取樣
取樣的概念與縮放直接相關。取樣的樣本越多,獲得的畫素就越多。過取樣也可以稱為縮放。這已在取樣和縮放教程中討論過。
但是,訊號數字化的過程並不僅限於取樣,還涉及另一個步驟,即量化。
什麼是量化?
量化與取樣相反。它在 y 軸上進行。當您對影像進行量化時,實際上是將訊號劃分為量子(分割槽)。
在訊號的 x 軸上是座標值,在 y 軸上是幅度。因此,對幅度的數字化稱為量化。
它是這樣完成的

您可以在此影像中看到,訊號已被量化為三個不同的級別。這意味著當我們對影像進行取樣時,我們實際上會收集大量的值,在量化中,我們將為這些值設定級別。在下圖中可以更清楚地看到這一點。

在上圖取樣中顯示的圖中,雖然已經進行了取樣,但它們在垂直方向上仍然跨越一個連續的灰度值範圍。在上圖中,這些垂直範圍的值已被量化為 5 個不同的級別或分割槽。從 0 黑色到 4 白色。這個級別可以根據您想要的影像型別而變化。
量化與灰度級之間的關係將在下面進一步討論。
量化與灰度解析度的關係
上圖所示的量化影像具有 5 個不同的灰度級別。這意味著由該訊號形成的影像將只有 5 種不同的顏色。它或多或少會是一張黑白影像,帶有一些灰色。現在,如果您想提高影像質量,您可以這樣做:增加級別或灰度級解析度。如果將此級別增加到 256,則表示您擁有灰度影像,這比簡單的黑白影像要好得多。
現在,256、5 或您選擇的任何級別都稱為灰度級。請記住我們在上一教程中討論過的灰度級解析度公式:
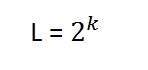
我們已經討論過,灰度級可以用兩種方式定義。這兩種方式是:
灰度級 = 每畫素位元數 (BPP)。(公式中的 k)
灰度級 = 每畫素級別數。
在這種情況下,灰度級等於 256。如果要計算位元數,只需將值代入公式即可。對於 256 個級別,我們有 256 種不同的灰色陰影和每畫素 8 位,因此影像將是灰度影像。
降低灰度級
現在我們將降低影像的灰度級以檢視對影像的影響。
例如
假設您有一張 8bpp 的影像,它有 256 個不同的級別。它是一張灰度影像,影像看起來像這樣。
256 個灰度級

現在我們將開始降低灰度級。我們首先將灰度級從 256 降低到 128。
128 個灰度級

將灰度級降低一半後,影像幾乎沒有影響。讓我們再降低一些。
64 個灰度級

仍然影響不大,那麼讓我們進一步降低級別。
32 個灰度級

令人驚訝的是,仍然有一些細微的影響。可能是因為這是愛因斯坦的照片,但讓我們進一步降低級別。
16 個灰度級

在這裡,影像最終顯示出受到級別影響。
8 個灰度級

4 個灰度級

現在,在將其進一步降低到 2 個級別之前,您可以很容易地看到影像由於降低灰度級而嚴重失真。現在我們將將其降低到 2 個級別,這只不過是一個簡單的黑白級別。這意味著影像將是簡單的黑白影像。
2 個灰度級

這是我們可以達到的最後一個級別,因為如果進一步降低,它將只是一張黑色影像,無法解釋。
輪廓
這裡有一個有趣的觀察結果,那就是當我們減少灰度級數時,影像中開始出現一種特殊型別的效果,這在 16 灰度級影像中可以清楚地看到。這種效應被稱為輪廓。
等偏好曲線
這種效應出現的原因在於等偏好曲線。它們將在我們下一節關於輪廓和等偏好曲線的教程中討論。
等偏好曲線
什麼是輪廓?
當我們減少影像中的灰度級數時,影像上會開始出現一些假顏色或邊緣。這在我們上一節關於量化的教程中已經顯示過。
讓我們來看一下。
假設我們有一張 8bpp 的影像(灰度影像),具有 256 種不同的灰色陰影或灰度級。

上圖有 256 種不同的灰色陰影。現在,當我們將其減少到 128,然後進一步減少到 64 時,影像或多或少相同。但是,當我們進一步將其減少到 32 個不同的級別時,我們得到了這樣的圖片

如果您仔細觀察,您會發現影像上開始出現這種效果。當我們進一步將其減少到 16 個級別時,這些效果更加明顯,我們得到了這樣的影像。

這些開始出現在影像上的線條被稱為輪廓,在上圖中非常明顯。
輪廓的增加和減少
隨著我們減少灰度級數,輪廓效應增加;隨著我們增加灰度級數,輪廓效應減少。兩者是反比關係。

與

這意味著更多的量化將導致更多的輪廓,反之亦然。但這總是這樣嗎?答案是否定的。這取決於下面討論的其他因素。
等偏好曲線
一項關於灰度級和輪廓效應的研究,其結果以曲線的形式繪製在圖表上,稱為等偏好曲線。
等偏好曲線現象表明,輪廓效應不僅取決於灰度級解析度的降低,還取決於影像細節。
研究的本質是
如果影像具有更多細節,與細節較少的影像相比,當灰度級量化時,輪廓效應會較晚出現在此影像上。
根據最初的研究,研究人員拍攝了這三張影像,並在所有三張影像中改變了灰度級解析度。
這些影像是



細節級別
第一張影像只包含一張臉,因此細節很少。第二張影像中還有一些其他物體,例如攝影師、他的相機、相機支架和背景物體等。而第三張影像比所有其他影像都包含更多細節。
實驗
所有影像的灰度級解析度都發生了變化,並要求觀眾主觀評價這三張影像。評價之後,根據結果繪製圖表。
結果
結果繪製在圖表上。圖表上的每條曲線都代表一張影像。x 軸上的值代表灰度級數,y 軸上的值代表每畫素位元數 (k)。
圖表如下所示。

根據該圖表,我們可以看到,第一張人臉影像比其他兩張影像更早地受到輪廓的影響。第二張攝影師影像在灰度級降低時,比第一張影像稍晚受到輪廓的影響。這是因為它比第一張影像包含更多細節。而第三張影像在比前兩張影像晚得多之後才受到輪廓的影響,即在 4 bpp 之後。這是因為這張影像包含更多細節。
結論
因此,對於更詳細的影像,等偏好曲線變得越來越垂直。這也意味著,對於細節量很大的影像,只需要很少的灰度級。
抖動概念
在關於量化和輪廓的最後兩個教程中,我們看到降低影像的灰度級會減少表示影像所需的顏色數量。如果灰度級降低到 2,則最後出現的影像沒有太多空間解析度或不那麼吸引人。
抖動
抖動是一個過程,透過該過程,我們可以創造出實際上不存在的顏色錯覺。這是透過畫素的隨機排列來實現的。
例如,考慮這張影像。

這是一張只有黑白畫素的影像。它的畫素按順序排列以形成下面顯示的另一張影像。請注意,畫素的排列方式發生了變化,但畫素的數量沒有變化。

為什麼要抖動?
為什麼我們需要抖動?答案在於它與量化的關係。
抖動與量化。
當我們將量化執行到最後一級時,我們看到最後一級(第 2 級)出現的影像如下所示。

現在,從這裡影像我們可以看到,圖片不是很清晰,特別是如果您觀察愛因斯坦影像的左臂和背部。此外,這張圖片也沒有太多關於愛因斯坦的資訊或細節。
現在,如果我們要將此影像更改為提供比這更多細節的影像,則必須執行抖動。
執行抖動。
首先,我們將處理閾值化。抖動通常用於改進閾值化。在閾值化過程中,銳利的邊緣出現在影像中梯度平滑的地方。
在閾值化中,我們只需選擇一個常數值。高於該值的所有畫素都被視為 1,低於該值的所有畫素都被視為 0。
閾值化後,我們得到了這張影像。

由於影像變化不大,因為此影像中的值已經是 0 和 1 或黑白。
現在我們對其執行一些隨機抖動。這是一些畫素的隨機排列。

我們得到了一張提供更多細節的影像,但對比度非常低。
因此,我們進行更多抖動以提高對比度。我們得到的影像是這個

現在我們將隨機抖動的概念與閾值混合在一起,我們得到了這樣的影像。

現在您看到,我們只是透過重新排列影像的畫素就獲得了所有這些影像。這種重新排列可以是隨機的,也可以根據某種度量來進行。
直方圖介紹
在討論直方圖在影像處理中的應用之前,我們將首先了解什麼是直方圖,它是如何使用的,然後舉一個直方圖的例子,以便更好地理解直方圖。
直方圖
直方圖是一個圖表。一個顯示任何事物頻率的圖表。直方圖通常具有條形圖,表示整個資料集中資料出現的頻率。
直方圖有兩個軸,x 軸和 y 軸。
x 軸包含必須計算其頻率的事件。
y 軸包含頻率。
條形圖的不同高度顯示資料的不同出現頻率。
直方圖通常看起來像這樣。

現在我們將看到構建此直方圖的示例
示例
考慮一個程式設計學生班級,你正在教他們 Python。
學期結束時,你得到了表中顯示的結果。但它非常混亂,沒有顯示你班級的整體結果。因此,你必須製作一個直方圖來顯示你班級的成績出現頻率。以下是你的操作方法。
成績單
| 姓名 | 等級 |
|---|---|
| John | A |
| Jack | D |
| Carter | B |
| Tommy | A |
| Lisa | C+ |
| Derek | A- |
| Tom | B+ |
成績單直方圖
現在你要做的是找到 x 軸和 y 軸上的內容。
有一點需要確定,即 y 軸包含頻率,那麼 x 軸上是什麼。x 軸包含必須計算其頻率的事件。在這種情況下,x 軸包含等級。

現在我們將看到如何在影像中使用直方圖。
影像的直方圖
影像的直方圖與其他直方圖一樣,也顯示頻率。但是影像直方圖顯示畫素強度值的頻率。在影像直方圖中,x 軸顯示灰度強度,y 軸顯示這些強度的頻率。
例如

上面愛因斯坦圖片的直方圖如下所示

直方圖的 x 軸顯示畫素值的範圍。因為它是一張 8 bpp 影像,這意味著它有 256 個灰度級別或灰色陰影。這就是為什麼 x 軸的範圍從 0 開始到 255 結束,間距為 50。而 y 軸是這些強度的計數。
從圖表中可以看到,大多數頻率高的條形圖位於前半部分,即較暗的部分。這意味著我們得到的影像較暗。這也可以從影像中得到證明。
直方圖的應用
直方圖在影像處理中有很多用途。正如上面討論的那樣,它的第一個用途是影像分析。我們只需檢視直方圖就可以預測影像的內容。這就像檢視人體骨骼的X光片一樣。
直方圖的第二個用途是用於亮度調整。直方圖在影像亮度方面應用廣泛。不僅用於亮度調整,直方圖還用於調整影像的對比度。
直方圖的另一個重要用途是影像均衡化。
最後但同樣重要的是,直方圖在閾值分割中應用廣泛。這主要用於計算機視覺。
亮度和對比度
亮度
亮度是一個相對的概念。它取決於你的視覺感知。由於亮度是一個相對的概念,因此亮度可以定義為光源輸出的能量相對於我們比較的光源而言的多少。在某些情況下,我們可以很容易地說影像很亮,而在某些情況下,則不容易感知。
例如
看看這兩張影像,比較一下哪一張更亮。

我們可以很容易地看出,右邊的影像比左邊的影像更亮。
但是,如果右邊的影像比左邊的影像更暗,那麼可以說左邊的影像比右邊的影像更亮。
如何使影像更亮。
亮度可以透過簡單地對影像矩陣進行加減來簡單地增加或減少。
考慮這幅5行5列的黑色影像

由於我們已經知道,每張影像背後都有一個包含畫素值的矩陣。此影像矩陣如下所示。
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
由於整個矩陣都填充為零,因此影像非常暗。
現在,我們將它與另一幅相同的黑色影像進行比較,看看這幅影像是否變亮了。

儘管如此,兩幅影像看起來仍然相同。為了使第二幅影像更亮,我們只需要將值1新增到表示它的矩陣的每個元素中。
我們將要做的是,簡單地將值1新增到影像1的矩陣的每個值中。新增後,影像1將如下所示。

現在,我們將再次將其與影像2進行比較,看看是否有任何區別。

我們看到,我們仍然無法分辨哪張影像更亮,因為兩張影像看起來都一樣。
現在我們將要做的是,我們將向影像1的矩陣的每個值新增50,看看影像變成了什麼樣子。
輸出如下所示。

現在,我們將再次將其與影像2進行比較。
現在您可以看到,影像1比影像2略亮。我們繼續,再向影像1的矩陣新增45個值,這次我們再次比較兩幅影像。

現在當你比較它時,你會發現影像1明顯比影像2亮。
它甚至比舊的影像1更亮。此時,影像1的矩陣在每個索引處都包含100,首先新增5,然後是50,然後是45。所以5 + 50 + 45 = 100。
對比度
對比度可以簡單地解釋為影像中最大和最小畫素強度之間的差異。
例如。
考慮亮度中的最終影像1。

此影像的矩陣是
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
此矩陣中的最大值為100。
此矩陣中的最小值為100。
對比度 = 最大畫素強度(減去)最小畫素強度
= 100(減去)100
= 0
0表示此影像的對比度為0。
影像變換
在討論什麼是影像變換之前,我們將討論什麼是變換。
變換。
變換是一個函式。一個在執行某些操作後將一個集合對映到另一個集合的函式。
數字影像處理系統
我們在入門教程中已經看到,在數字影像處理中,我們將開發一個系統,其輸入將是一幅影像,輸出也將是一幅影像。並且系統將對輸入影像進行一些處理,並將其處理後的影像作為輸出。如下圖所示。
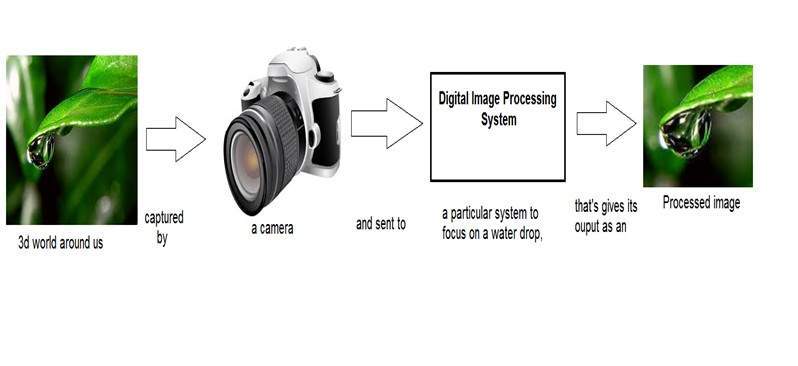
現在,在這個數字系統內部應用的處理影像並將其轉換為輸出的函式可以稱為變換函式。
因為它顯示了變換或關係,即影像1如何轉換為影像2。
影像變換。
考慮這個等式
G(x,y) = T{ f(x,y) }
在這個等式中,
F(x,y) = 需要應用變換函式的輸入影像。
G(x,y) = 輸出影像或處理後的影像。
T是變換函式。
輸入影像和處理後的輸出影像之間的這種關係也可以表示為。
s = T (r)
其中r實際上是f(x,y)在任何點的畫素值或灰度強度。s是g(x,y)在任何點的畫素值或灰度強度。
基本的灰度級變換已經在我們的基本灰度級變換教程中討論過。
現在我們將討論一些非常基本變換函式。
示例
考慮這個變換函式。
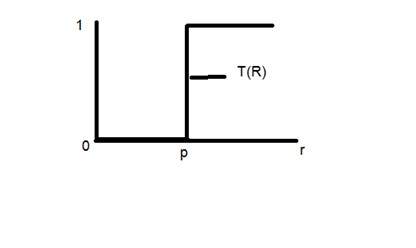
讓我們取點r為256,點p為127。考慮這幅影像為一幅1bpp影像。這意味著我們只有兩個強度級別,即0和1。在這種情況下,圖中所示的變換可以解釋為:
所有低於127(點p)的畫素強度值均為0,表示黑色。所有高於127的畫素強度值均為1,表示白色。但在127的精確點上,傳輸發生了突然變化,因此我們無法判斷在該精確點上的值為0還是1。
從數學上講,此變換函式可以表示為
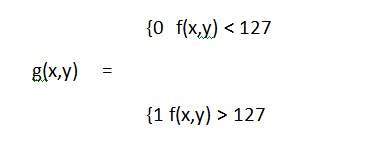
考慮另一個這樣的變換
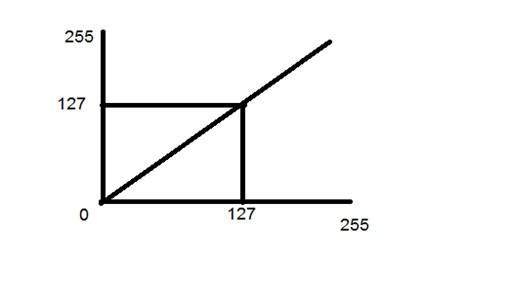
現在,如果你看一下這個特定的圖表,你會看到輸入影像和輸出影像之間有一個直線過渡線。
它表明,對於輸入影像的每個畫素或強度值,輸出影像都有相同的強度值。這意味著輸出影像是輸入影像的精確複製品。
它可以用數學表示為
g(x,y) = f(x,y)
在這種情況下,輸入和輸出影像如下所示。

直方圖滑動
直方圖的基本概念已在直方圖入門教程中討論過。但我們將在此簡要介紹直方圖。
直方圖
直方圖只不過是一個顯示資料出現頻率的圖表。直方圖在影像處理中有很多用途,我們將在此討論其中一個用途,稱為直方圖滑動。
直方圖滑動。
在直方圖滑動中,我們只需簡單地將整個直方圖向右或向左移動。由於直方圖向右或向左移動或滑動,影像中可以看到明顯的變化。在本教程中,我們將使用直方圖滑動來操縱亮度。
術語,即:亮度已在我們的亮度和對比度入門教程中討論過。但我們將在此簡要定義一下。
亮度
亮度是一個相對的概念。亮度可以定義為特定光源發出的光強度。
對比度
對比度可以定義為影像中最大和最小畫素強度之間的差異。
滑動直方圖
使用直方圖滑動增加亮度

此影像的直方圖如下所示。

此直方圖的y軸是頻率或計數。在x軸上,我們有灰度值。從上面的直方圖可以看出,那些計數超過700的灰度強度位於前半部分,即朝向較暗的部分。這就是為什麼我們得到一幅有點暗的影像。
為了使其變亮,我們將直方圖向右滑動,或朝向較亮的部分滑動。為此,我們需要至少向此影像新增50個值。因為我們可以從上面的直方圖中看到,此影像也具有0畫素強度,即純黑色。因此,如果我們將0新增到50,我們將把位於0強度的所有值移到50強度,其餘的值將相應地移動。
讓我們試試。
在向每個畫素強度新增50後,我們得到了以下結果。
影像如下所示。

它的直方圖如下所示。

讓我們比較這兩幅影像及其直方圖,看看發生了什麼變化。

結論
從新的直方圖中我們可以清楚地看到,所有畫素值都已向右移動,其效果可以在新影像中看到。
使用直方圖滑動降低亮度
現在,如果我們要降低這幅新影像的亮度,以至於舊的影像看起來更亮,我們必須從新影像的所有矩陣中減去一些值。我們將減去的值為80。因為我們已經向原始影像添加了50,並且得到了一幅新的更亮的影像,現在如果我們要使其變暗,我們必須至少從中減去超過50的值。
從新影像中減去80後,我們得到了以下結果。

結論
從新影像的直方圖可以清楚地看出,所有畫素值都已向右移動,因此,可以從影像中驗證新影像更暗,並且現在原始影像與這幅新影像相比看起來更亮。
直方圖拉伸
我們在直方圖入門教程中討論的直方圖的另一個優點是對比度增強。
有兩種增強對比度的方法。第一種稱為直方圖拉伸,它可以增加對比度。第二種稱為直方圖均衡化,它可以增強對比度,這已在我們直方圖均衡化教程中討論過。
在討論直方圖拉伸以增加對比度之前,我們將簡要定義對比度。
對比度。
對比度是最大和最小畫素強度之間的差異。
考慮此影像。

此影像的直方圖如下所示。
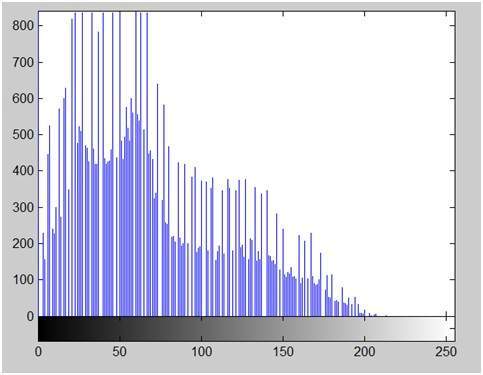
現在我們從這張影像中計算對比度。
對比度 = 225。
現在我們將增加影像的對比度。
增加影像的對比度
用於拉伸影像直方圖以增加對比度的公式為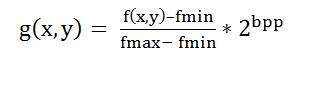
該公式需要找到最小和最大畫素強度乘以灰度級別。在我們的例子中,影像是8bpp,因此灰度級別為256。
最小值為0,最大值為225。因此,在我們的例子中,公式為
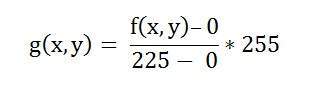
其中f(x,y)表示每個畫素強度的值。對於影像中的每個f(x,y),我們將計算這個公式。
完成此操作後,我們將能夠增強對比度。
應用直方圖拉伸後,將顯示以下影像。

下圖顯示了此影像的拉伸直方圖。
注意直方圖的形狀和對稱性。直方圖現在被拉伸或擴充套件了。請看一看。
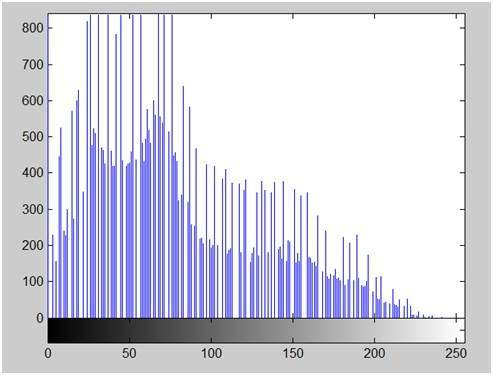
在這種情況下,影像的對比度可以計算為
對比度 = 240
因此,可以說影像的對比度增加了。
注意:這種增加對比度的方法並不總是有效,在某些情況下會失敗。
直方圖拉伸的失敗
正如我們所討論的,該演算法在某些情況下會失敗。這些情況包括影像中存在畫素強度為 0 和 255 的影像。
因為當影像中存在畫素強度為 0 和 255 時,它們就會成為最小和最大畫素強度,從而破壞了這樣的公式。
原始公式
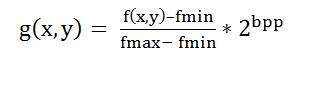
將失敗情況的值代入公式
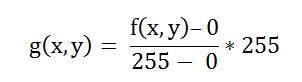
簡化該表示式得到
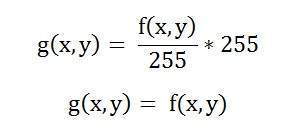
這意味著輸出影像等於處理後的影像。這意味著此影像沒有進行直方圖拉伸。
機率論簡介
PMF 和 CDF 這兩個術語都屬於機率和統計。現在你腦海中應該出現的問題是,為什麼我們要學習機率。這是因為 PMF 和 CDF 這兩個概念將在下一個直方圖均衡教程中使用。因此,如果你不知道如何計算 PMF 和 CDF,你就無法對你的影像應用直方圖均衡。
.什麼是 PMF?
PMF 代表機率質量函式。顧名思義,它給出資料集中每個數字的機率,或者可以說它基本上給出每個元素的計數或頻率。
如何計算 PMF
我們將透過兩種不同的方式計算 PMF。首先是從矩陣,因為在下一個教程中,我們必須從矩陣計算 PMF,而影像只不過是一個二維矩陣。
然後我們將舉另一個例子,在這個例子中我們將從直方圖計算 PMF。
考慮這個矩陣。
| 1 | 2 | 7 | 5 | 6 |
| 7 | 2 | 3 | 4 | 5 |
| 0 | 1 | 5 | 7 | 3 |
| 1 | 2 | 5 | 6 | 7 |
| 6 | 1 | 0 | 3 | 4 |
現在,如果我們要計算這個矩陣的 PMF,我們將這樣操作。
首先,我們將取矩陣中的第一個值,然後我們將計算這個值在整個矩陣中出現的次數。計數後,它們可以表示在直方圖中,也可以表示在下表中。
PMF
| 0 | 2 | 2/25 |
| 1 | 4 | 4/25 |
| 2 | 3 | 3/25 |
| 3 | 3 | 3/25 |
| 4 | 2 | 2/25 |
| 5 | 4 | 4/25 |
| 6 | 3 | 3/25 |
| 7 | 4 | 4/25 |
請注意,計數的總和必須等於值的總數。
從直方圖計算 PMF
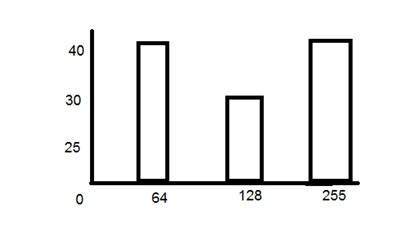
上圖直方圖顯示了 8 位/畫素影像的灰度值的頻率。
現在,如果我們必須計算它的 PMF,我們將簡單地檢視垂直軸上每個條形的計數,然後將其除以總計數。
所以上面直方圖的 PMF 是這個。
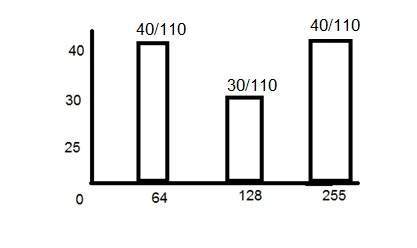
需要注意的另一個重要點是,它不是單調遞增的。因此,為了使其單調遞增,我們將計算其 CDF。
什麼是 CDF?
CDF 代表累積分佈函式。它是一個計算 PMF 計算的所有值的累積和的函式。它基本上是對前一個值的求和。
它是如何計算的?
我們將使用直方圖計算 CDF。以下是它的操作方法。考慮上面顯示的顯示 PMF 的直方圖。
由於這個直方圖不是單調遞增的,所以我們將使其單調遞增。
我們將簡單地保持第一個值不變,然後在第二個值中,我們將新增第一個值,依此類推。
以下是上述 PMF 函式的 CDF。
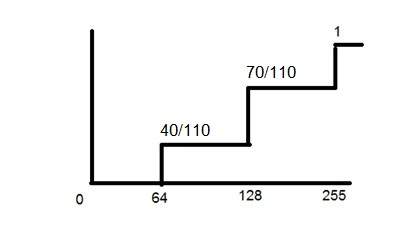
現在你可以從上面的圖表中看到,PMF 的第一個值保持不變。PMF 的第二個值加到第一個值中並放在 128 上。PMF 的第三個值加到 CDF 的第二個值中,得到 110/110,等於 1。
而且現在,該函式呈單調遞增趨勢,這是直方圖均衡的必要條件。
直方圖均衡中 PMF 和 CDF 的用法
直方圖均衡。
直方圖均衡將在下一個教程中討論,但下面簡要介紹了直方圖均衡。
直方圖均衡用於增強影像的對比度。
PMF 和 CDF 都用於直方圖均衡,如本教程開頭所述。在直方圖均衡中,第一步和第二步分別是 PMF 和 CDF。由於在直方圖均衡中,我們必須均衡影像的所有畫素值。因此,PMF 幫助我們計算影像中每個畫素值的機率。CDF 給出了這些值的累積和。此外,將此 CDF 乘以級別,以找到新的畫素強度,這些強度對映到舊值中,並且直方圖得到均衡。
直方圖均衡
我們已經看到可以使用直方圖拉伸來增加對比度。在本教程中,我們將瞭解如何使用直方圖均衡來增強對比度。
在執行直方圖均衡之前,你必須瞭解均衡直方圖中使用的兩個重要概念。這兩個概念稱為 PMF 和 CDF。
它們在我們的 PMF 和 CDF 教程中進行了討論。請訪問它們以便成功掌握直方圖均衡的概念。
直方圖均衡
直方圖均衡用於增強對比度。不必總是增加對比度。在某些情況下,直方圖均衡可能會更糟糕。在這些情況下,對比度會降低。
讓我們以以下影像為例,作為一個簡單的影像來開始直方圖均衡。
影像

此影像的直方圖
此影像的直方圖顯示如下。

現在我們將對其執行直方圖均衡。
PMF
首先,我們必須計算此影像中所有畫素的 PMF(機率質量函式)。如果你不知道如何計算 PMF,請訪問我們的 PMF 計算教程。
CDF
我們的下一步涉及計算 CDF(累積分佈函式)。同樣,如果你不知道如何計算 CDF,請訪問我們的 CDF 計算教程。
根據灰度級計算 CDF
例如,考慮一下,第二步計算的 CDF 看起來像這樣。
| 灰度級值 | CDF |
|---|---|
| 0 | 0.11 |
| 1 | 0.22 |
| 2 | 0.55 |
| 3 | 0.66 |
| 4 | 0.77 |
| 5 | 0.88 |
| 6 | 0.99 |
| 7 | 1 |
然後在這個步驟中,你將把 CDF 值乘以(灰度級(減去)1)。
假設我們有一個 3 bpp 影像。那麼我們擁有的級別數為 8。1 減去 8 為 7。因此我們將 CDF 乘以 7。這是我們乘法後得到的結果。
| 灰度級值 | CDF | CDF * (級別-1) |
|---|---|---|
| 0 | 0.11 | 0 |
| 1 | 0.22 | 1 |
| 2 | 0.55 | 3 |
| 3 | 0.66 | 4 |
| 4 | 0.77 | 5 |
| 5 | 0.88 | 6 |
| 6 | 0.99 | 6 |
| 7 | 1 | 7 |
現在是最後一步,我們必須將新的灰度級值對映到畫素數。
假設我們的舊灰度級值具有這些畫素數。
| 灰度級值 | 頻率 |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 10 |
| 5 | 12 |
| 6 | 14 |
| 7 | 16 |
現在,如果我們將新值對映到,那麼這就是我們得到的結果。
| 灰度級值 | 新的灰度級值 | 頻率 |
|---|---|---|
| 0 | 0 | 2 |
| 1 | 1 | 4 |
| 2 | 3 | 6 |
| 3 | 4 | 8 |
| 4 | 5 | 10 |
| 5 | 6 | 12 |
| 6 | 6 | 14 |
| 7 | 7 | 16 |
現在將這些新值對映到直方圖上,你就完成了。
讓我們將此技術應用於我們的原始影像。應用後,我們得到了以下影像及其直方圖。
直方圖均衡影像

此影像的累積分佈函式

直方圖均衡直方圖

比較兩個直方圖和影像

結論
從影像中可以清楚地看出,新的影像對比度得到了增強,並且其直方圖也得到了均衡。這裡還有一個需要注意的重要一點,即在直方圖均衡過程中,直方圖的整體形狀會發生變化,而在直方圖拉伸中,直方圖的整體形狀保持不變。
灰度級變換
在我們的基本變換教程中,我們討論了一些基本變換。在本教程中,我們將瞭解一些基本灰度級變換。
影像增強
與未增強影像相比,增強影像可提供更好的對比度和更詳細的影像。影像增強具有廣泛的應用。它用於增強醫學影像、遙感影像、衛星影像等。
變換函式如下所示
s = T ( r )
其中 r 是輸入影像的畫素,s 是輸出影像的畫素。T 是一個變換函式,它將 r 的每個值對映到 s 的每個值。影像增強可以透過下面討論的灰度級變換來完成。
灰度級變換
有三種基本灰度級變換。
線性
對數
冪律
這些轉換的整體圖形顯示如下。

線性變換
首先,我們將研究線性變換。線性變換包括簡單的恆等變換和負變換。恆等變換已在我們的影像變換教程中討論過,但此處對該變換進行了簡要說明。
恆等變換由直線表示。在這個變換中,輸入影像的每個值都直接對映到輸出影像的另一個值。這會導致輸入影像和輸出影像相同。因此被稱為恆等變換。它顯示如下

負變換
第二個線性變換是負變換,它是恆等變換的逆。在負變換中,輸入影像的每個值都從 L-1 中減去並對映到輸出影像。
結果大致如下。
輸入影像

輸出影像

在這種情況下,進行了以下轉換。
s = (L – 1) – r
由於愛因斯坦的輸入影像是一個 8 bpp 影像,因此此影像中的級別數為 256。將 256 代入方程,我們得到:
s = 255 – r
因此,每個值都減去 255,並且上面顯示了結果影像。所以發生的情況是,較亮的畫素變暗,較暗的影像變亮。它導致影像反轉。
下圖所示。

對數變換
對數變換包含兩種型別的變換:對數變換和反對數變換。
對數變換
對數變換可以用以下公式定義:
s = c log(r + 1).
其中,s 和 r 分別是輸出影像和輸入影像的畫素值,c 是一個常數。在輸入影像的每個畫素值中新增 1,是因為如果影像中存在畫素強度為 0 的畫素,則 log(0) 等於無窮大。因此新增 1,使最小值至少為 1。
在對數變換過程中,影像中的暗畫素比高畫素值擴充套件得更多。高畫素值在對數變換中會壓縮。這會導致以下影像增強效果。
對數變換中的 c 值可以調整您所需的增強型別。
輸入影像

對數變換影像

反對數變換與對數變換相反。
冪律變換
冪律變換還包含兩種變換,包括 n 次冪變換和 n 次方根變換。這些變換可以用以下表達式表示:
s=cr^γ
符號 γ 稱為伽馬值,因此這種變換也稱為伽馬變換。
γ 值的變化會改變影像的增強效果。不同的顯示裝置/顯示器具有其自身的伽馬校正,這就是為什麼它們以不同的強度顯示影像的原因。
這種型別的變換用於增強不同型別顯示裝置的影像。不同顯示裝置的伽馬值不同。例如,CRT 的伽馬值在 1.8 到 2.5 之間,這意味著 CRT 上顯示的影像較暗。
伽馬校正。
s=cr^γ
s=cr^(1/2.5)
這裡顯示了具有不同伽馬值的同一影像。
例如
伽馬 = 10

伽馬 = 8

伽馬 = 6

卷積的概念
本教程介紹了訊號與系統的一個非常重要的概念。我們將完整地討論卷積。它是什麼?為什麼需要它?我們可以用它實現什麼?
我們將從影像處理的基礎知識開始討論卷積。
什麼是影像處理。
正如我們在影像處理教程的介紹和訊號與系統中所討論的那樣,影像處理或多或少是對訊號與系統的研究,因為影像只不過是一個二維訊號。
我們還討論了,在影像處理中,我們正在開發一個系統,其輸入是影像,輸出也是影像。這可以用圖示表示為:

上圖中標註為“數字影像處理系統”的框可以認為是一個黑盒。
它可以更好地表示為:

我們目前達到了什麼階段
到目前為止,我們已經討論了兩種重要的影像處理方法。或者換句話說,到目前為止,我們的黑盒以兩種不同的方式工作。
兩種不同的影像處理方法是:
圖表(直方圖)

此方法稱為直方圖處理。我們在之前的教程中詳細討論了它,用於提高對比度、影像增強、亮度等。
變換函式

此方法稱為變換,我們討論了不同型別的變換和一些灰度變換。
另一種處理影像的方法
在這裡,我們將討論另一種處理影像的方法。這種方法稱為卷積。通常用於影像處理的黑盒(系統)是 LTI 系統或線性時不變系統。線性是指輸出始終是線性的,既不是對數也不是指數或其他任何形式。時間不變是指在時間上保持不變的系統。
所以現在我們將使用第三種方法。它可以表示為:

它可以用兩種數學方式表示
g(x,y) = h(x,y) * f(x,y)
它可以解釋為“掩膜與影像的卷積”。
或者
g(x,y) = f(x,y) * h(x,y)
它可以解釋為“影像與掩膜的卷積”。
可以用兩種方式表示這一點,因為卷積運算子 (*) 是可交換的。h(x,y) 是掩膜或濾波器。
什麼是掩膜?
掩膜也是一個訊號。它可以用一個二維矩陣來表示。掩膜通常是 1x1、3x3、5x5、7x7 等階數。掩膜必須是奇數階,否則無法找到掩膜的中心。為什麼我們需要找到掩膜的中心?答案在下面“如何執行卷積?”主題中。
如何執行卷積?
為了對影像執行卷積,應採取以下步驟。
僅翻轉一次掩膜(水平和垂直)
將掩膜滑到影像上。
將對應的元素相乘,然後相加
重複此過程,直到計算出影像的所有值。
卷積示例
讓我們執行一些卷積。第一步是翻轉掩膜。
掩膜
讓我們將我們的掩膜設為:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
水平翻轉掩膜
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
垂直翻轉掩膜
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
影像
讓我們考慮一個這樣的影像:
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
卷積
將掩膜在影像上卷積。它是這樣完成的。將掩膜的中心放在影像的每個元素上。將對應的元素相乘,然後相加,並將結果貼上到放置掩膜中心的影像元素上。

紅色框是掩膜,橙色值是掩膜的值。黑色框和值屬於影像。現在對於影像的第一個畫素,其值將計算為:
第一個畫素 = (5*2) + (4*4) + (2*8) + (1*10)
= 10 + 16 + 16 + 10
= 52
將 52 放到原始影像的第一個索引處,並對影像的每個畫素重複此過程。
為什麼使用卷積
卷積可以實現前兩種影像處理方法無法實現的功能。這些包括模糊、銳化、邊緣檢測、降噪等。
掩膜的概念
什麼是掩膜。
掩膜是一個濾波器。掩膜的概念也稱為空間濾波。掩膜也稱為濾波。在這個概念中,我們只處理直接在影像上執行的濾波操作。
下面顯示了一個示例掩膜
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
什麼是濾波。
濾波過程也稱為將掩膜與影像卷積。由於此過程與卷積相同,因此濾波器掩膜也稱為卷積掩膜。
它是如何完成的。
濾波和應用掩膜的一般過程包括將濾波器掩膜在影像中逐點移動。在原始影像的每個點 (x,y) 處,濾波器的響應由預定義的關係計算。所有濾波器值都是預定義的,並且是標準的。
濾波器的型別
一般有兩種型別的濾波器。一種稱為線性濾波器或平滑濾波器,另一種稱為頻域濾波器。
為什麼使用濾波器?
濾波器應用於影像的多種用途。兩種最常見的用途如下:
濾波器用於模糊和降噪
濾波器用於邊緣檢測和銳化
模糊和降噪
濾波器最常用於模糊和降噪。模糊用於預處理步驟,例如在大型物體提取之前從影像中去除小的細節。
用於模糊的掩膜。
用於模糊的常用掩膜是:
盒式濾波器
加權平均濾波器
在模糊過程中,我們減少影像中的邊緣內容,並儘量使不同畫素強度之間的過渡儘可能平滑。
藉助模糊也可以進行降噪。
邊緣檢測和銳化
掩膜或濾波器也可用於影像中的邊緣檢測和提高影像銳度。
什麼是邊緣。
我們也可以說,影像中突然變化的不連續性稱為邊緣。影像中明顯的過渡稱為邊緣。下面顯示了一幅帶有邊緣的圖片。
原始圖片。

帶有邊緣的相同圖片

模糊的概念
我們在之前的掩膜概念教程中簡要介紹了模糊,但我們將在本文中正式討論它。
模糊
在模糊中,我們只是簡單地模糊影像。如果我們能夠正確地感知影像中的所有物體及其形狀,則影像看起來更清晰或更詳細。例如,帶有面部的影像,當我們能夠非常清晰地識別眼睛、耳朵、鼻子、嘴唇、額頭等時,看起來很清晰。物體的形狀是由於其邊緣造成的。因此,在模糊中,我們只是簡單地減少邊緣內容,並使從一種顏色到另一種顏色的過渡非常平滑。
模糊與縮放。
您可能在縮放影像時看到過模糊的影像。當您使用畫素複製縮放影像並且縮放因子增加時,您會看到模糊的影像。此影像的細節也較少,但這並不是真正的模糊。
因為在縮放中,您向影像新增新的畫素,這會增加影像中畫素的總數,而在模糊中,普通影像和模糊影像的畫素數量保持不變。
模糊影像的常見示例。

濾波器的型別。
模糊可以透過多種方式實現。用於執行模糊的常用濾波器型別是:
均值濾波器
加權平均濾波器
高斯濾波器
在這三種濾波器中,我們將在這裡討論前兩種,高斯濾波器將在後續教程中討論。
均值濾波器。
均值濾波器也稱為盒式濾波器和平均濾波器。均值濾波器具有以下屬性:
它必須是奇數階的
所有元素的總和應為 1
所有元素都應相同
如果我們遵循此規則,則對於 3x3 的掩膜,我們將得到以下結果:
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
由於它是一個 3x3 的掩膜,這意味著它有 9 個單元格。所有元素之和應等於 1 的條件可以透過將每個值除以 9 來實現,因為:
1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 = 9/9 = 1
3x3 掩膜對影像的結果如下所示:
原始影像

模糊影像

結果可能不是很清晰。讓我們增加模糊度。可以透過增加掩膜的大小來增加模糊度。掩膜越大,模糊度越大。因為使用更大的掩膜,可以處理更多的畫素,並定義一個平滑的過渡。
5x5 掩膜對影像的結果如下所示:
原始影像

模糊影像

同樣,如果我們增加掩膜大小,模糊度會更大,結果如下所示:
7x7 掩膜對影像的結果如下所示:
原始影像

模糊影像

9x9 掩膜對影像的結果如下所示:
原始影像

模糊影像

11x11 掩膜對影像的結果如下所示:
原始影像

模糊影像

加權平均濾波器。
在加權平均濾波器中,我們賦予中心值更大的權重。因此,中心值的貢獻比其他值更大。由於加權平均濾波,我們實際上可以控制模糊度。
加權平均濾波器的屬性是:
它必須是奇數階的
所有元素的總和應為 1
中心元素的權重應大於所有其他元素
濾波器 1
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 1 | 1 |
滿足兩個屬性(1 和 3)。但是屬性 2 未滿足。因此,為了滿足該屬性,我們將簡單地將整個濾波器除以 10 或乘以 1/10。
濾波器 2
| 1 | 1 | 1 |
| 1 | 10 | 1 |
| 1 | 1 | 1 |
除數 = 18。
邊緣檢測的概念
我們在掩膜介紹教程中簡要討論了邊緣檢測。我們將在本文中正式討論邊緣檢測。
什麼是邊緣。
影像中不連續性的突然變化稱為邊緣。影像中顯著的過渡也稱為邊緣。
邊緣型別。
通常邊緣分為三種類型
水平邊緣
垂直邊緣
對角線邊緣
為什麼要檢測邊緣。
影像的大部分形狀資訊都包含在邊緣中。因此,我們首先檢測影像中的這些邊緣,然後使用這些濾波器增強包含邊緣的影像區域,從而提高影像的清晰度,使影像更加清晰。
以下是一些我們將在下節教程中討論的邊緣檢測運算元。
Prewitt運算元
Sobel運算元
Robinson羅盤掩膜
Krisch羅盤掩膜
拉普拉斯運算元。
以上提到的所有濾波器都是線性濾波器或平滑濾波器。
Prewitt運算元
Prewitt運算元用於檢測水平和垂直邊緣。
Sobel運算元
Sobel運算元與Prewitt運算元非常相似。它也是一個微分掩膜,用於邊緣檢測。它也計算水平和垂直方向的邊緣。
Robinson羅盤掩膜
該運算元也稱為方向掩膜。在這個運算元中,我們取一個掩膜,將其旋轉到所有8個主要羅盤方向,以計算每個方向的邊緣。
Kirsch羅盤掩膜
Kirsch羅盤掩膜也是一個微分掩膜,用於查詢邊緣。Kirsch掩膜也用於計算所有方向的邊緣。
拉普拉斯運算元。
拉普拉斯運算元也是一個微分運算元,用於查詢影像中的邊緣。拉普拉斯運算元是二階微分掩膜。它可以進一步細分為正拉普拉斯運算元和負拉普拉斯運算元。
所有這些掩膜都用於查詢邊緣。有些查詢水平和垂直方向的邊緣,有些只查詢一個方向的邊緣,有些查詢所有方向的邊緣。接下來的概念是銳化,可以在從影像中提取邊緣後進行。
銳化
銳化與模糊相反。在模糊處理中,我們減少邊緣內容;在銳化中,我們增加邊緣內容。因此,為了增加影像中的邊緣內容,我們必須首先找到邊緣。
可以使用上述任何一種方法或任何運算元來查詢邊緣。找到邊緣後,我們將這些邊緣新增到影像中,這樣影像將具有更多邊緣,並且看起來更清晰。
這是銳化影像的一種方法。
銳化後的影像如下所示。
原始影像

銳化影像

Prewitt運算元
Prewitt運算元用於影像邊緣檢測。它檢測兩種型別的邊緣
水平邊緣
垂直邊緣
邊緣是透過使用影像對應畫素強度之間的差異計算的。所有用於邊緣檢測的掩膜也稱為微分掩膜。因為正如我們在這個教程系列中多次提到的那樣,影像也是一種訊號,因此只能使用微分來計算訊號的變化。這就是為什麼這些運算元也稱為微分運算元或微分掩膜。
所有微分掩膜都應具有以下屬性
掩膜中應存在相反的符號。
掩膜的總和應等於零。
權重越大,邊緣檢測效果越好。
Prewitt運算元為我們提供了兩個掩膜,一個用於檢測水平方向的邊緣,另一個用於檢測垂直方向的邊緣。
垂直方向
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
上述掩膜將找到垂直方向的邊緣,這是因為垂直方向的列為零。當您將此掩膜與影像進行卷積時,它將為您提供影像中的垂直邊緣。
工作原理
當我們將此掩膜應用於影像時,它會突出顯示垂直邊緣。它的工作原理就像一階導數一樣,計算邊緣區域中畫素強度的差異。由於中心列為零,因此它不包含影像的原始值,而是計算該邊緣周圍左右畫素值的差值。這增加了邊緣強度,並使其與原始影像相比得到增強。
水平方向
| -1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
上述掩膜將找到水平方向的邊緣,這是因為零列位於水平方向。當您將此掩膜與影像進行卷積時,它將突出顯示影像中的水平邊緣。
工作原理
此掩膜將突出顯示影像中的水平邊緣。它也基於上述掩膜的原理,計算特定邊緣畫素強度之間的差異。由於掩膜的中心行由零組成,因此它不包含影像中邊緣的原始值,而是計算特定邊緣上下畫素強度的差異。從而增加了強度的突然變化,使邊緣更加清晰。上述兩個掩膜都遵循微分掩膜的原理。兩個掩膜中都有相反的符號,並且兩個掩膜的總和等於零。第三個條件不適用於此運算元,因為上述兩個掩膜都是標準化的,我們不能更改其中的值。
現在是時候看看這些掩膜的實際效果了
示例影像
下面是一個示例圖片,我們將一次應用上述兩個掩膜。

應用垂直掩膜後
將垂直掩膜應用於上述示例影像後,將獲得以下影像。此影像包含垂直邊緣。透過與水平邊緣圖片進行比較,您可以更準確地判斷。

應用水平掩膜後
將水平掩膜應用於上述示例影像後,將獲得以下影像。

比較
您可以看到,在應用垂直掩膜的第一張圖片中,所有垂直邊緣都比原始影像更清晰。同樣,在第二張圖片中,我們應用了水平掩膜,結果所有水平邊緣都清晰可見。這樣,您可以看到我們可以從影像中檢測水平和垂直邊緣。
Sobel運算元
Sobel運算元與Prewitt運算元非常相似。它也是一個微分掩膜,用於邊緣檢測。與Prewitt運算元一樣,Sobel運算元也用於檢測影像中的兩種邊緣。
垂直方向
水平方向
與Prewitt運算元的區別
主要區別在於,在Sobel運算元中,掩膜的係數不是固定的,可以根據我們的需要進行調整,除非它們不違反微分掩膜的任何屬性。
以下是Sobel運算元的垂直掩膜
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
此掩膜的工作方式與Prewitt運算元的垂直掩膜完全相同。只有一個區別,即它在第一列和第三列的中心具有“2”和“-2”值。當應用於影像時,此掩膜將突出顯示垂直邊緣。
工作原理
當我們將此掩膜應用於影像時,它會突出顯示垂直邊緣。它的工作原理就像一階導數一樣,計算邊緣區域中畫素強度的差異。
由於中心列為零,因此它不包含影像的原始值,而是計算該邊緣周圍左右畫素值的差值。並且第一列和第三列的中心值分別為2和-2。
這為邊緣區域周圍的畫素值賦予了更大的權重。這增加了邊緣強度,並使其與原始影像相比得到增強。
以下是Sobel運算元的水平掩膜
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
上述掩膜將找到水平方向的邊緣,這是因為零列位於水平方向。當您將此掩膜與影像進行卷積時,它將突出顯示影像中的水平邊緣。唯一的區別是它在第一行和第三行的中心元素為2和-2。
工作原理
此掩膜將突出顯示影像中的水平邊緣。它也基於上述掩膜的原理,計算特定邊緣畫素強度之間的差異。由於掩膜的中心行由零組成,因此它不包含影像中邊緣的原始值,而是計算特定邊緣上下畫素強度的差異。從而增加了強度的突然變化,使邊緣更加清晰。
現在是時候看看這些掩膜的實際效果了
示例影像
下面是一個示例圖片,我們將一次應用上述兩個掩膜。

應用垂直掩膜後
將垂直掩膜應用於上述示例影像後,將獲得以下影像。

應用水平掩膜後
將水平掩膜應用於上述示例影像後,將獲得以下影像

比較
您可以看到,在應用垂直掩膜的第一張圖片中,所有垂直邊緣都比原始影像更清晰。同樣,在第二張圖片中,我們應用了水平掩膜,結果所有水平邊緣都清晰可見。
這樣,您可以看到我們可以從影像中檢測水平和垂直邊緣。此外,如果您將Sobel運算元的結果與Prewitt運算元的結果進行比較,您會發現與Prewitt運算元相比,Sobel運算元可以找到更多邊緣或使邊緣更清晰。
這是因為在Sobel運算元中,我們為邊緣周圍的畫素強度分配了更大的權重。
對掩膜應用更大的權重
現在我們還可以看到,如果我們對掩膜應用更大的權重,它將為我們獲得更多邊緣。此外,正如教程開頭提到的那樣,Sobel運算元沒有固定的係數,因此這裡還有另一個加權運算元
| -1 | 0 | 1 |
| -5 | 0 | 5 |
| -1 | 0 | 1 |
如果您將此掩膜的結果與Prewitt垂直掩膜的結果進行比較,很明顯,此掩膜將比Prewitt掩膜提供更多邊緣,這僅僅是因為我們在掩膜中分配了更大的權重。
Robinson羅盤掩膜
Robinson羅盤掩膜是另一種用於邊緣檢測的微分掩膜。該運算元也稱為方向掩膜。在此運算元中,我們取一個掩膜,並將其旋轉到所有8個主要羅盤方向,如下所示
北
西北
西
西南
南
東南
東
東北
沒有固定的掩膜。您可以取任何掩膜,並且必須將其旋轉以在所有上述方向上查詢邊緣。所有掩膜都基於零列的方向進行旋轉。
例如,讓我們看看以下位於北方向的掩膜,然後將其旋轉以製作所有方向掩膜。
北方向掩膜
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
西北方向掩膜
| 0 | 1 | 2 |
| -1 | 0 | 1 |
| -2 | -1 | 0 |
西方向掩膜
| 1 | 2 | 1 |
| 0 | 0 | 0 |
| -1 | -2 | -1 |
西南方向掩膜
| 2 | 1 | 0 |
| 1 | 0 | -1 |
| 0 | -1 | -2 |
南方向掩膜
| 1 | 0 | -1 |
| 2 | 0 | -2 |
| 1 | 0 | -1 |
東南方向掩膜
| 0 | -1 | -2 |
| 1 | 0 | -1 |
| 2 | 1 | 0 |
東方向掩膜
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
東北方向掩膜
| -2 | -1 | 0 |
| -1 | 0 | 1 |
| 0 | 1 | 2 |
您可以看到,所有方向都基於零方向覆蓋。每個掩膜都將為您提供其方向上的邊緣。現在讓我們看看所有上述掩膜的結果。假設我們有一張示例圖片,我們必須從中找到所有邊緣。這是我們的示例圖片
示例圖片

現在我們將所有上述濾波器應用於此影像,並將獲得以下結果。
北方向邊緣

西北方向邊緣

西方向邊緣

西南方向邊緣

南方向邊緣

東南方向邊緣

東方向邊緣

東北方向邊緣

您可以看到,透過應用所有上述掩膜,您將獲得所有方向的邊緣。結果也取決於影像。假設有一張影像沒有任何東北方向的邊緣,那麼該掩膜將無效。
Krisch羅盤掩膜
Kirsch羅盤掩膜也是一個用於查詢邊緣的微分掩膜。這與Robinson羅盤掩膜類似,可以在羅盤的八個方向上查詢邊緣。Robinson和Kirsch羅盤掩膜之間的唯一區別在於,在Kirsch中,我們有一個標準掩膜,但在Kirsch中,我們可以根據自己的要求更改掩膜。
藉助Kirsch羅盤掩膜,我們可以在以下八個方向上查詢邊緣。
北
西北
西
西南
南
東南
東
東北
我們採用一個符合導數掩膜所有屬性的標準掩膜,然後旋轉它來查詢邊緣。
例如,讓我們看看以下位於北方向的掩膜,然後將其旋轉以製作所有方向掩膜。
北方向掩膜
| -3 | -3 | 5 |
| -3 | 0 | 5 |
| -3 | -3 | 5 |
西北方向掩膜
| -3 | 5 | 5 |
| -3 | 0 | 5 |
| -3 | -3 | -3 |
西方向掩膜
| 5 | 5 | 5 |
| -3 | 0 | -3 |
| -3 | -3 | -3 |
西南方向掩膜
| 5 | 5 | -3 |
| 5 | 0 | -3 |
| -3 | -3 | -3 |
南方向掩膜
| 5 | -3 | -3 |
| 5 | 0 | -3 |
| 5 | -3 | -3 |
東南方向掩膜
| -3 | -3 | -3 |
| 5 | 0 | -3 |
| 5 | 5 | -3 |
東方向掩膜
| -3 | -3 | -3 |
| -3 | 0 | -3 |
| 5 | 5 | 5 |
東北方向掩膜
| -3 | -3 | -3 |
| -3 | 0 | 5 |
| -3 | 5 | 5 |
可以看到,所有方向都被覆蓋了,每個掩膜都會給出它自身方向的邊緣。為了幫助你更好地理解這些掩膜的概念,我們將在真實的影像上應用它。假設我們有一張樣本圖片,我們需要從中找到所有邊緣。這是我們的樣本圖片
示例圖片

現在我們將所有上述濾波器應用於此影像,並將獲得以下結果。
北方向邊緣

西北方向邊緣

西方向邊緣

西南方向邊緣

南方向邊緣

東南方向邊緣

東方向邊緣

東北方向邊緣

您可以看到,透過應用所有上述掩膜,您將獲得所有方向的邊緣。結果也取決於影像。假設有一張影像沒有任何東北方向的邊緣,那麼該掩膜將無效。
拉普拉斯運算元
拉普拉斯運算元也是一個微分運算元,用於查詢影像中的邊緣。拉普拉斯運算元和其它運算元(如 Prewitt、Sobel、Robinson 和 Kirsch)的主要區別在於,這些都是一階微分掩膜,而拉普拉斯運算元是二階微分掩膜。在這個掩膜中,我們有兩個進一步的分類,一個是正拉普拉斯運算元,另一個是負拉普拉斯運算元。
拉普拉斯運算元和其它運算元的另一個區別是,與其它運算元不同,拉普拉斯運算元不會以任何特定方向提取邊緣,而是按以下分類提取邊緣。
內邊緣
外邊緣
讓我們看看拉普拉斯運算元是如何工作的。
正拉普拉斯運算元
在正拉普拉斯運算元中,我們有一個標準掩膜,其中掩膜的中心元素應為負數,掩膜的角元素應為零。
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
正拉普拉斯運算元用於提取影像中的外邊緣。
負拉普拉斯運算元
在負拉普拉斯運算元中,我們也有一個標準掩膜,其中中心元素應為正數。所有角元素都應為零,掩膜中其餘所有元素都應為 -1。
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
負拉普拉斯運算元用於提取影像中的內邊緣
工作原理
拉普拉斯運算元是一個微分運算元;它的用途是突出影像中灰度級的間斷,並試圖弱化灰度級變化緩慢的區域。此操作的結果是產生這樣的影像:在黑暗的背景上具有灰色的邊緣線和其他間斷。這會在影像中產生內邊緣和外邊緣
重要的是如何將這些濾波器應用於影像。記住,我們不能在同一影像上同時應用正拉普拉斯運算元和負拉普拉斯運算元。我們必須只應用一個,但要記住的是,如果我們將正拉普拉斯運算元應用於影像,那麼我們將結果影像從原始影像中減去以獲得銳化影像。類似地,如果我們應用負拉普拉斯運算元,那麼我們必須將結果影像新增到原始影像以獲得銳化影像。
讓我們將這些濾波器應用於影像,看看它將如何從影像中獲得內邊緣和外邊緣。假設我們有以下樣本影像。
示例影像

應用正拉普拉斯運算元後
應用正拉普拉斯運算元後,我們將得到以下影像。

應用負拉普拉斯運算元後
應用負拉普拉斯運算元後,我們將得到以下影像。

頻域介紹
我們已經處理了多個領域的影像。現在我們正在頻域中處理訊號(影像)。由於傅立葉級數和頻域純粹是數學,所以我們將盡量減少數學部分,更多地關注它在數字影像處理中的應用。
頻域分析
到目前為止,在我們分析訊號的所有域中,我們都是相對於時間來分析的。但在頻域中,我們不是相對於時間分析訊號,而是相對於頻率分析。
空間域和頻域的區別。
在空間域中,我們直接處理影像。影像畫素的值隨場景而變化。而在頻域中,我們處理的是空間域中畫素值變化的速率。
為簡單起見,讓我們這樣說。
空間域

在簡單的空間域中,我們直接處理影像矩陣。而在頻域中,我們處理影像的方式是這樣的。
頻域
我們首先將影像變換為其頻率分佈。然後我們的黑盒系統執行它必須執行的任何處理,在這種情況下,黑盒的輸出不是影像,而是一種變換。執行逆變換後,它被轉換為影像,然後在空間域中檢視。
它可以圖示為

這裡我們使用了變換這個詞。它到底是什麼意思?
變換。
可以使用稱為變換的數學運算子將訊號從時域轉換為頻域。有很多型別的變換可以做到這一點。其中一些如下所示。
傅立葉級數
傅立葉變換
拉普拉斯變換
Z 變換
在所有這些中,我們將在下一個教程中詳細討論傅立葉級數和傅立葉變換。
頻率成分
空間域中的任何影像都可以用頻域表示。但是這些頻率到底是什麼意思呢?
我們將頻率成分分為兩個主要成分。
高頻成分
高頻成分對應於影像中的邊緣。
低頻成分
影像中的低頻成分對應於平滑區域。
傅立葉級數和變換
在最後一個關於頻域分析的教程中,我們討論了傅立葉級數和傅立葉變換用於將訊號轉換為頻域。
傅立葉
傅立葉是1822年的數學家。他提出了傅立葉級數和傅立葉變換,將訊號轉換為頻域。
傅立葉級數
傅立葉級數簡單地說,週期性訊號可以表示為正弦和餘弦的和,當乘以一定的權重時。它進一步指出,週期性訊號可以分解成具有以下屬性的更進一步的訊號。
訊號是正弦和餘弦
訊號是彼此的諧波
它可以圖示為
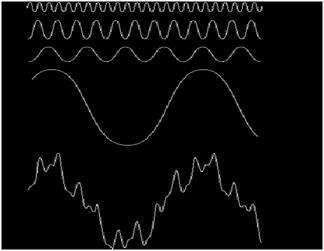
在上圖訊號中,最後一個訊號實際上是所有上述訊號的總和。這是傅立葉的想法。
它是如何計算的。
正如我們在頻域中看到的,為了在頻域中處理影像,我們需要首先使用它將其轉換為頻域,並且我們必須取輸出的逆變換以將其轉換回空間域。這就是為什麼傅立葉級數和傅立葉變換都有兩個公式的原因。一個用於轉換,一個用於將其轉換回空間域。
傅立葉級數
傅立葉級數可以用這個公式表示。
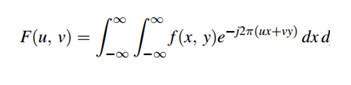
反變換可以用這個公式計算。
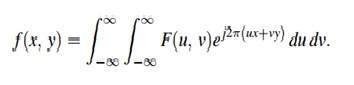
傅立葉變換
傅立葉變換簡單地說,曲線下面積有限的非週期訊號也可以表示為正弦和餘弦的積分,在乘以一定的權重後。
傅立葉變換有許多廣泛的應用,包括影像壓縮(例如 JPEG 壓縮)、濾波和影像分析。
傅立葉級數和變換的區別
雖然傅立葉級數和傅立葉變換都是由傅立葉提出的,但它們之間的區別在於,傅立葉級數應用於週期性訊號,而傅立葉變換應用於非週期性訊號。
哪個應用於影像。
現在的問題是,傅立葉級數還是傅立葉變換應用於影像。這個問題的答案在於影像是什麼。影像是非週期性的。由於影像是非週期性的,因此使用傅立葉變換將其轉換為頻域。
離散傅立葉變換。
由於我們處理的是影像,實際上是數字影像,因此對於數字影像,我們將使用離散傅立葉變換。

考慮上述正弦曲線的傅立葉項。它包括三件事。
空間頻率
幅度
相位
空間頻率直接與影像的亮度相關。正弦曲線的幅度直接與對比度相關。對比度是最大和最小畫素強度之間的差異。相位包含顏色資訊。
二維離散傅立葉變換的公式如下。
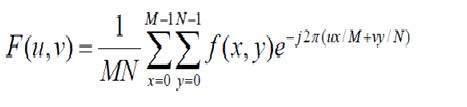
離散傅立葉變換實際上是取樣的傅立葉變換,因此它包含一些表示影像的樣本。在上式中,f(x,y)表示影像,F(u,v)表示離散傅立葉變換。二維逆離散傅立葉變換的公式如下。
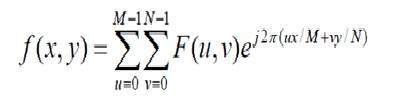
逆離散傅立葉變換將傅立葉變換轉換回影像
考慮這個訊號。
現在我們將看到一個影像,我們將計算它的 FFT 幅度譜,然後計算移位的 FFT 幅度譜,然後取該移位譜的對數。
原始影像

傅立葉變換幅度譜

移位的傅立葉變換

移位的幅度譜

卷積定理
在最後一個教程中,我們討論了頻域中的影像。在本教程中,我們將定義頻域和影像(空間域)之間的關係。
例如
考慮這個例子。

頻域中的同一影像可以表示為。

那麼影像或空間域與頻域之間有什麼關係呢?這種關係可以用一個稱為卷積定理的定理來解釋。
卷積定理
空間域和頻域之間的關係可以透過卷積定理建立。
卷積定理可以表示為。

它可以表述為:空間域中的卷積等於頻域中的濾波,反之亦然。
頻域中的濾波可以表示如下

濾波步驟如下。
第一步,我們必須對空間域中的影像進行一些預處理,這意味著增加其對比度或亮度
然後我們將進行影像的離散傅立葉變換
然後我們將對離散傅立葉變換進行中心化,因為我們將把離散傅立葉變換從角點移到中心
然後我們將應用濾波,這意味著我們將用濾波函式乘以傅立葉變換
然後我們將再次將 DFT 從中心移到角點
最後一步是進行逆離散傅立葉變換,將結果從頻域轉換回空間域
並且這個後處理步驟是可選的,就像預處理一樣,我們只是增加了影像的外觀。
濾波器
頻域中濾波器的概念與卷積中掩膜的概念相同。
將影像轉換為頻域後,在濾波過程中應用一些濾波器來對影像執行不同型別的處理。處理包括模糊影像、銳化影像等。
用於這些目的的常用濾波器型別是
理想高通濾波器
理想低通濾波器
高斯高通濾波器
高斯低通濾波器
在下一個教程中,我們將詳細討論濾波器。
高通濾波器與低通濾波器
在最後一個教程中,我們簡要地討論了濾波器。在本教程中,我們將詳細討論它們。在討論之前,讓我們先談談掩膜。掩膜的概念已經在我們的卷積和掩膜教程中討論過。
模糊掩膜與微分掩膜。
我們將對模糊掩膜和微分掩膜進行比較。
模糊掩膜
模糊掩膜具有以下屬性。
模糊掩膜中的所有值均為正值
所有值的總和等於 1
使用模糊掩碼可以減少邊緣內容。
隨著掩碼尺寸的增加,平滑效果會越明顯。
導數掩碼
導數掩碼具有以下特性。
導數掩碼包含正值和負值。
導數掩碼中所有值的總和等於零。
導數掩碼會增加邊緣內容。
隨著掩碼尺寸的增加,邊緣內容也會增加。
模糊掩碼和導數掩碼與高通濾波器和低通濾波器的關係。
模糊掩碼和導數掩碼與高通濾波器和低通濾波器的關係可以簡單地定義為:
模糊掩碼也稱為低通濾波器。
導數掩碼也稱為高通濾波器。
高頻分量和低頻分量
高頻分量表示邊緣,而低頻分量表示平滑區域。
理想低通濾波器和理想高通濾波器
這是一個常見的低通濾波器示例。
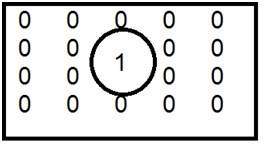
當內部值為1,外部值為0時,得到模糊影像。隨著內部值1的尺寸增加,模糊程度增加,邊緣內容減少。
這是一個常見的高通濾波器示例。
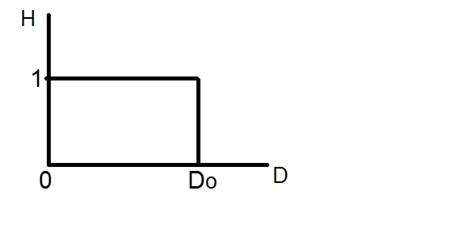
當內部值為0時,得到邊緣,得到素描影像。頻域中的理想低通濾波器如下所示。

理想低通濾波器可以用圖形表示為:
現在讓我們將此濾波器應用於實際影像,看看結果。
示例影像。

頻域影像

將濾波器應用於此影像

結果影像

同樣,理想高通濾波器也可以應用於影像。但結果顯然不同,因為低通濾波器減少了邊緣內容,而高通濾波器增加了邊緣內容。
高斯低通濾波器和高斯高通濾波器
高斯低通濾波器和高斯高通濾波器可以最小化理想低通濾波器和高通濾波器中出現的問題。
這個問題被稱為吉布斯現象(ringing effect)。這是因為在某些點上,一種顏色到另一種顏色的過渡無法精確定義,因此在該點出現吉布斯現象。
請看這個圖表。
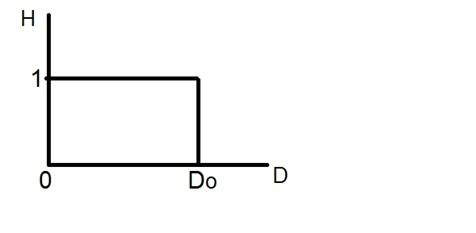
這是理想低通濾波器的表示。在Do的精確點,無法確定其值為0還是1。因此,在該點出現吉布斯現象。
因此,為了減少理想低通濾波器和理想高通濾波器中出現的效果,引入了以下高斯低通濾波器和高斯高通濾波器。
高斯低通濾波器
濾波和低通的概念保持不變,只是過渡變得不同,並且更加平滑。
高斯低通濾波器可以表示為:
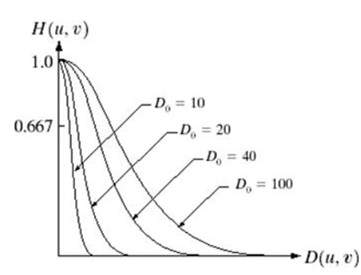
注意平滑的曲線過渡,因此在每個點上,Do的值都可以精確定義。
高斯高通濾波器
高斯高通濾波器的概念與理想高通濾波器相同,但與理想高通濾波器相比,過渡更加平滑。
顏色空間介紹
在本教程中,我們將討論顏色空間。
什麼是顏色空間?
顏色空間是在影像處理和訊號系統中用於各種目的的不同型別的顏色模式。一些常見的顏色空間包括:
RGB
CMYK
YUV
YIQ
Y'CbCr
HSV
RGB
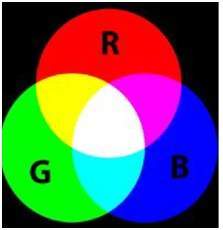
RGB是最廣泛使用的顏色空間,我們已經在之前的教程中討論過它。RGB代表紅、綠、藍。
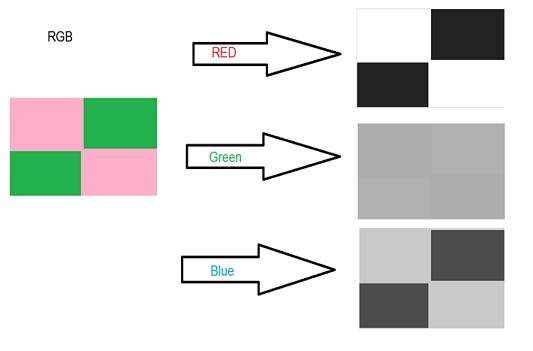
RGB模型指出,每個彩色影像實際上是由三個不同的影像組成的:紅色影像、綠色影像和藍色影像。普通的灰度影像可以用一個矩陣定義,但彩色影像實際上是由三個不同的矩陣組成的。
一個彩色影像矩陣 = 紅色矩陣 + 綠色矩陣 + 藍色矩陣
這在下面的示例中可以最好地看到。
RGB的應用
RGB模型的常見應用包括:
陰極射線管 (CRT)
液晶顯示器 (LCD)
等離子顯示器或LED顯示器,例如電視
計算機顯示器或大型螢幕
CMYK

RGB到CMYK轉換
RGB到CMYK的轉換使用以下方法完成。
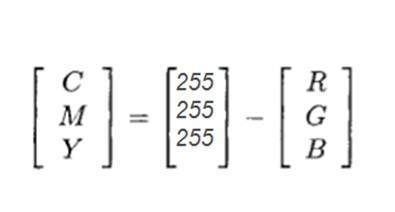
假設你有一個彩色影像,這意味著你具有三個不同的紅色、綠色和藍色陣列。如果你想將其轉換為CMYK,你需要這樣做:用最大級別數減1的結果減去每個矩陣,並將結果分別填充到相應的CMYK矩陣中。
YUV
YUV根據一個亮度 (Y') 和兩個色度 (UV) 分量定義顏色空間。YUV顏色模型用於以下複合彩色影片標準:
NTSC(國家電視系統委員會)
PAL(相位交替線)
SECAM(Sequential couleur a amemoire,法語,意為“帶記憶的順序彩色”)

Y'CbCr
Y'CbCr顏色模型包含Y'(亮度分量),Cb和Cr是藍色差和紅色差色度分量。
它不是絕對顏色空間。它主要用於數字系統。
其常見應用包括JPEG和MPEG壓縮。
Y'UV通常用作Y'CbCr的術語,但它們是完全不同的格式。兩者之間的主要區別在於前者是模擬的,而後者是數字的。

JPEG壓縮介紹
在我們上一節關於影像壓縮的教程中,我們討論了一些用於壓縮的技術。
我們將討論JPEG壓縮,這是一種有失真壓縮,因為最終會丟失一些資料。
讓我們首先討論什麼是影像壓縮。
影像壓縮
影像壓縮是對數字影像進行資料壓縮的方法。
影像壓縮的主要目標是:
以有效的方式儲存資料
以有效的方式傳輸資料
影像壓縮可以是有損的或無損的。
JPEG壓縮
JPEG代表聯合影像專家組。它是影像壓縮的第一個國際標準。它如今被廣泛使用。它可以是有損的,也可以是無損的。但我們今天將要討論的技術是有失真壓縮技術。
JPEG壓縮的工作原理
第一步是將影像分成塊,每個塊的尺寸為8 x 8。

讓我們記錄一下,這個8x8影像包含以下值。
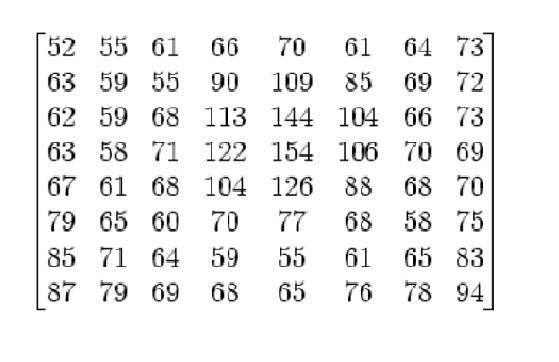
畫素強度的範圍現在是0到255。我們將範圍更改為-128到127。
從每個畫素值中減去128得到-128到127的畫素值。從每個畫素值中減去128後,我們得到以下結果。

現在我們將使用此公式進行計算。
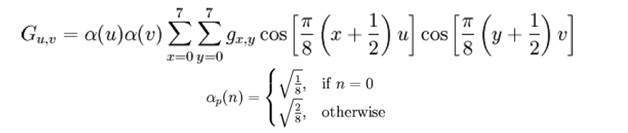
結果儲存在例如A(j,k)矩陣中。
JPEG壓縮使用一個標準矩陣,該矩陣稱為亮度矩陣。
此矩陣如下所示
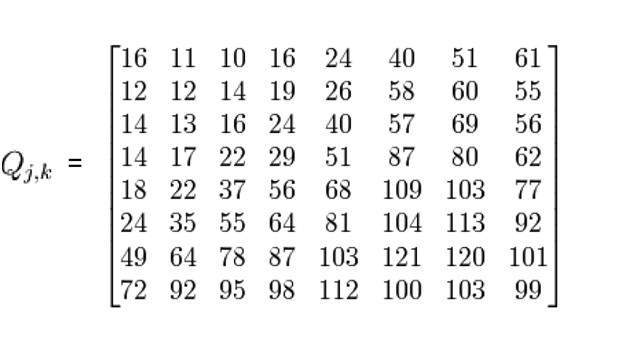
應用以下公式
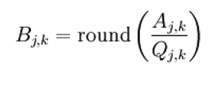
應用後我們得到這個結果。

現在我們將執行JPEG壓縮中使用的真正技巧,即ZIG-ZAG移動。上面矩陣的zig zag序列如下所示。你必須執行zig zag,直到你找到前面全是零為止。因此,我們的影像現在被壓縮了。

JPEG壓縮總結
第一步是將影像轉換為Y'CbCr,只選擇Y'通道並將其分解為8 x 8塊。然後從第一個塊開始,將範圍對映到-128到127。之後,你必須找到矩陣的離散傅立葉變換。此結果應進行量化。最後一步是以zig zag的方式應用編碼,並執行此操作直到找到所有零。
儲存這個一維陣列,你就完成了。
注意:你必須對所有8 x 8塊重複此過程。
光學字元識別
光學字元識別通常縮寫為OCR。它包括將手寫、打字文字的掃描影像機械和電氣地轉換為機器文字。這是將印刷文字數字化的一種常用方法,以便可以對其進行電子搜尋、更緊湊地儲存、線上顯示以及用於機器翻譯、文字轉語音和文字挖掘等機器過程。
近年來,光學字元識別 (OCR) 技術已應用於各個行業,徹底改變了文件管理流程。OCR使掃描文件不僅僅是影像檔案,而是變成了完全可搜尋的文件,其文字內容可被計算機識別。藉助OCR,人們在將重要文件輸入電子資料庫時,不再需要手動重新輸入。相反,OCR會自動提取相關資訊並將其輸入。結果是更準確、更高效的資訊處理,時間更短。
光學字元識別有多個研究領域,但最常見的領域如下:
銀行業務
OCR的用途因不同領域而異。一個廣為人知的應用是在銀行業務中,OCR用於處理支票而無需人工干預。支票可以插入機器中,其上的文字會立即被掃描,並轉移正確的金額。這項技術對於列印支票來說幾乎已經完善,對於手寫支票也相當準確,儘管偶爾需要人工確認。總的來說,這減少了許多銀行的等待時間。
盲人和視障人士
OCR研究開始的主要因素之一是科學家想要製造一臺能夠大聲朗讀書籍給盲人聽的計算機或裝置。在這項研究中,科學家制造了平板掃描器,我們最常將其稱為文件掃描器。
法律部門
在法律行業,也出現了一場將紙質檔案數字化的重大變革。為了節省空間並消除篩選紙質檔案盒子的需要,檔案被掃描並輸入計算機資料庫。OCR技術進一步簡化了這一流程,使檔案可進行文字搜尋,以便在資料庫中更容易找到和使用它們。法律專業人員現在可以快速、輕鬆地訪問大量電子格式的檔案,只需輸入幾個關鍵詞即可找到它們。
零售行業
條形碼識別技術也與OCR相關。我們在日常生活中就能看到這項技術的應用。
其他應用
OCR廣泛應用於許多其他領域,包括教育、金融和政府機構。OCR使無數文字能夠線上獲取,為學生節省了資金,並促進了知識共享。許多企業使用發票影像應用程式來跟蹤財務記錄,防止付款積壓。在政府機構和獨立組織中,OCR簡化了資料收集和分析等流程。隨著技術的不斷發展,OCR技術的應用也越來越多,包括手寫識別技術的日益普及。
計算機視覺和計算機圖形學
計算機視覺
計算機視覺關注的是利用計算機軟體和硬體模擬和複製人類視覺。正式定義的話,計算機視覺是一門研究如何根據場景中存在的結構特性,從其二維影像重建、解釋和理解三維場景的學科。
為了理解和模擬人類視覺系統的運作,它需要以下領域的知識。
計算機科學
電子工程
數學
生理學
生物學
認知科學
計算機視覺層次結構
計算機視覺分為以下三個基本類別:
低層視覺:包括用於特徵提取的影像處理。
中層視覺:包括目標識別和三維場景解釋。
高層視覺:包括對場景的概念性描述,例如活動、意圖和行為。
相關領域
計算機視覺與以下領域有很大的重疊:
影像處理:它專注於影像操作。
模式識別:它研究各種分類模式的技術。
攝影測量:它關注的是從影像中獲取精確的測量結果。
計算機視覺與影像處理
影像處理研究影像到影像的轉換。影像處理的輸入和輸出都是影像。
計算機視覺是從影像中構建對物理物件的明確、有意義的描述。計算機視覺的輸出是對三維場景中結構的描述或解釋。
應用示例
機器人技術
醫學
安全
交通運輸
工業自動化
機器人技術應用
定位——自動確定機器人位置
導航
避障
組裝(銷孔配合、焊接、噴漆)
操作(例如PUMA機器人機械手)
人機互動(HRI):智慧機器人與人互動併為人類服務
醫學應用
分類和檢測(例如病變或細胞分類和腫瘤檢測)
二維/三維分割
三維人體器官重建(MRI或超聲波)
視覺引導機器人手術
工業自動化應用
工業檢測(缺陷檢測)
組裝
條形碼和包裝標籤讀取
物體分揀
文件理解(例如OCR)
安全應用
生物識別技術(虹膜、指紋、面部識別)
監控——檢測某些可疑活動或行為
交通運輸應用
自動駕駛車輛
安全,例如駕駛員警覺性監控
計算機圖形學
計算機圖形學是指使用計算機建立的圖形,以及計算機對影像資料的表示,特別是藉助專門的圖形硬體和軟體。正式地說,計算機圖形學是幾何物件(建模)及其影像(渲染)的建立、操作和儲存。
計算機圖形學領域隨著計算機圖形學硬體的出現而發展起來。如今,計算機圖形學幾乎應用於各個領域。許多強大的工具已被開發用於視覺化資料。當公司開始在電子遊戲中使用計算機圖形學時,該領域變得越來越流行。如今,它是一個數十億美元的產業,也是計算機圖形學發展的主要驅動力。一些常見的應用領域如下:
計算機輔助設計(CAD)
演示圖形
3D動畫
教育和培訓
圖形使用者介面
計算機輔助設計
用於建築物、汽車、飛機和許多其他產品的的設計。
用於建立虛擬現實系統。
演示圖形
通常用於總結財務、統計資料。
用於生成幻燈片。
3D動畫
皮克斯、夢工廠等公司在電影行業大量使用。
用於在遊戲中新增特效。
教育和培訓
物理系統的計算機生成模型。
醫學視覺化
3D MRI
牙科和骨骼掃描
飛行員等培訓模擬器。
圖形使用者介面
用於製作圖形使用者介面物件,如按鈕、圖示和其他元件。