傅立葉級數和變換

在上一篇關於頻域分析的教程中，我們討論了傅立葉級數和傅立葉變換用於將訊號轉換為頻域。

傅立葉

傅立葉是1822年的數學家。他提出了傅立葉級數和傅立葉變換，用於將訊號轉換為頻域。

傅立葉級數簡單地說，週期訊號可以表示為正弦和餘弦的和，並乘以一定的權重。它進一步指出，週期訊號可以分解成具有以下屬性的更進一步的訊號。

它可以用圖示的方式表示為

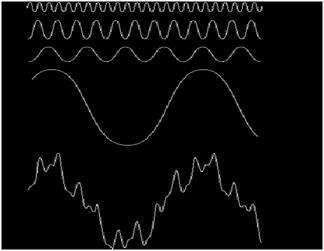
在上圖中，最後一個訊號實際上是所有上面訊號的總和。這是傅立葉的想法。

正如我們在頻域中看到的，為了在頻域中處理影像，我們需要首先使用它將其轉換為頻域，並且我們必須取輸出的逆變換以將其轉換回空間域。這就是為什麼傅立葉級數和傅立葉變換都有兩個公式。一個用於轉換，另一個用於將其轉換回空間域。

傅立葉級數可以用這個公式表示。

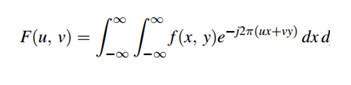
逆變換可以透過這個公式計算。

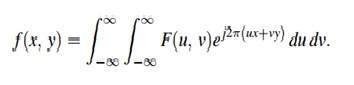
傅立葉變換簡單地說，曲線下面積有限的非週期訊號也可以表示為正弦和餘弦的積分，並乘以一定的權重。

傅立葉變換有很多廣泛的應用，包括影像壓縮（例如JPEG壓縮）、濾波和影像分析。

儘管傅立葉級數和傅立葉變換都是由傅立葉提出的，但它們之間的區別在於傅立葉級數應用於週期訊號，而傅立葉變換應用於非週期訊號。

現在問題是，哪一個應用於影像，傅立葉級數還是傅立葉變換。這個問題的答案在於影像的本質。影像是非週期的。由於影像是非週期的，因此使用傅立葉變換將其轉換為頻域。

由於我們正在處理影像，事實上是數字影像，因此對於數字影像，我們將使用離散傅立葉變換。

考慮上面正弦波的傅立葉項。它包含三件事。

空間頻率與影像的亮度直接相關。正弦波的幅度與對比度直接相關。對比度是最大和最小畫素強度之間的差異。相位包含顏色資訊。

二維離散傅立葉變換的公式如下所示。

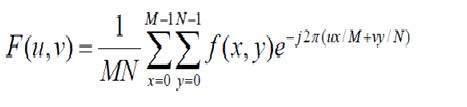
離散傅立葉變換實際上是傅立葉變換的取樣，因此它包含一些表示影像的樣本。在上式中，f(x,y)表示影像，F(u,v)表示離散傅立葉變換。二維離散傅立葉逆變換的公式如下所示。

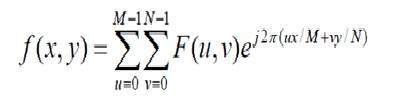
離散傅立葉逆變換將傅立葉變換轉換回影像。

現在我們將看到一個影像，我們將計算它的FFT幅度譜，然後計算移位的FFT幅度譜，然後取該移位譜的對數。

列印頁面