訊號取樣技術

---

---

有三種類型的取樣技術

• 脈衝取樣。

• 自然取樣。

• 平頂取樣。

脈衝取樣

脈衝取樣可以透過將輸入訊號 x(t) 與週期為 'T' 的脈衝序列 $\Sigma_{n=-\infty}^{\infty}\delta(t-nT)$ 相乘來實現。這裡，脈衝的幅度隨輸入訊號 x(t) 的幅度變化。取樣器的輸出由下式給出

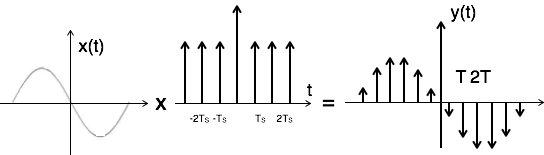
$y(t) = x(t) ×$ 脈衝序列

$= x(t) × \Sigma_{n=-\infty}^{\infty} \delta(t-nT)$

$ y(t) = y_{\delta} (t) = \Sigma_{n=-\infty}^{\infty}x(nt) \delta(t-nT)\,...\,... 1 $

為了得到取樣訊號的頻譜，考慮對等式 1 兩邊進行傅立葉變換

$Y(\omega) = {1 \over T} \Sigma_{n=-\infty}^{\infty} X(\omega - n \omega_s ) $

這稱為理想取樣或脈衝取樣。在實踐中你無法使用它，因為脈衝寬度不可能為零，並且在實踐中不可能產生脈衝序列。

自然取樣

自然取樣類似於脈衝取樣，只是脈衝序列被週期為 T 的脈衝序列所取代。即你將輸入訊號 x(t) 乘以脈衝序列 $\Sigma_{n=-\infty}^{\infty} P(t-nT)$，如下所示

取樣器的輸出為

$y(t) = x(t) \times \text{脈衝序列}$

$= x(t) \times p(t) $

$= x(t) \times \Sigma_{n=-\infty}^{\infty} P(t-nT)\,...\,...(1) $

p(t) 的指數傅立葉級數表示可以表示為

$p(t) = \Sigma_{n=-\infty}^{\infty} F_n e^{j n\omega_s t}\,...\,...(2) $

$= \Sigma_{n=-\infty}^{\infty} F_n e^{j 2 \pi nf_s t} $

其中 $F_n= {1 \over T} \int_{-T \over 2}^{T \over 2} p(t) e^{-j n \omega_s t} dt$

$= {1 \over TP}(n \omega_s)$

將 F_n 值代入等式 2

$ \therefore p(t) = \Sigma_{n=-\infty}^{\infty} {1 \over T} P(n \omega_s)e^{j n \omega_s t}$

$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)e^{j n \omega_s t}$

將 p(t) 代入等式 1

$y(t) = x(t) \times p(t)$

$= x(t) \times {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)\,e^{j n \omega_s t} $

$y(t) = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t} $

為了得到取樣訊號的頻譜，考慮對兩邊進行傅立葉變換。

$F.T\, [ y(t)] = F.T [{1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t}]$

$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,F.T\,[ x(t)\, e^{j n \omega_s t} ] $

根據頻移特性

$F.T\,[ x(t)\, e^{j n \omega_s t} ] = X[\omega-n\omega_s] $

$ \therefore\, Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,X[\omega-n\omega_s] $

平頂取樣

在傳輸過程中，在傳輸脈衝的頂部會引入噪聲，如果脈衝呈平頂狀，則可以很容易地去除這些噪聲。這裡，樣本的頂部是平坦的，即它們具有恆定的幅度。因此，它被稱為平頂取樣或實際取樣。平頂取樣利用了取樣保持電路。

理論上，取樣訊號可以透過矩形脈衝 p(t) 與理想取樣訊號（例如 y_δ(t)）進行卷積來獲得，如圖所示

即 $ y(t) = p(t) \times y_\delta (t)\, ... \, ...(1) $

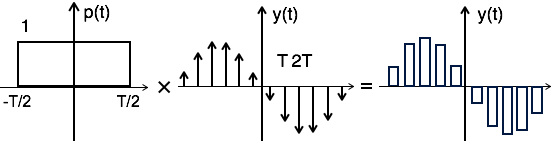
為了得到取樣頻譜，考慮對等式 1 兩邊進行傅立葉變換

$Y[\omega] = F.T\,[P(t) \times y_\delta (t)] $

根據卷積特性，

$Y[\omega] = P(\omega)\, Y_\delta (\omega)$

這裡 $P(\omega) = T Sa({\omega T \over 2}) = 2 \sin \omega T/ \omega$

奈奎斯特率

它是訊號可以轉換為樣本並可以無失真恢復的最小取樣率。

奈奎斯特率 f_N = 2f_m hz

奈奎斯特間隔 = ${1 \over fN}$ = $ {1 \over 2fm}$ 秒。

帶通訊號的取樣

對於帶通訊號，帶通訊號 X[ω] 的頻譜在 f₁ ≤ f ≤ f₂ 範圍之外的頻率為 0。頻率 f₁ 始終大於零。此外，當 f_s > 2f₂ 時沒有混疊效應。但它有兩個缺點

• 取樣率與 f₂ 成正比。這在實踐中存在侷限性。

• 取樣訊號頻譜存在頻譜間隙。

為了克服這一點，帶通定理指出，當取樣頻率 f_s < 2f₂ 時，輸入訊號 x(t) 可以轉換為其樣本並可以無失真恢復。

此外，

$$ f_s = {1 \over T} = {2f_2 \over m} $$

其中 m 是小於 ${f_2 \over B}$ 的最大整數

且 B 為訊號的頻寬。如果 f₂=KB，則

$$ f_s = {1 \over T} = {2KB \over m} $$

對於頻寬為 2f_m 的帶通訊號，最小取樣率 f_s= 2 B = 4f_m，

取樣訊號的頻譜由 $Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty}\,X[ \omega - 2nB]$ 給出