卷積與相關

卷積

卷積是一種數學運算，用於表達線性時不變 (LTI) 系統的輸入和輸出之間的關係。它將 LTI 系統的輸入、輸出和衝激響應關聯起來，如下所示：

$$ y (t) = x(t) * h(t) $$

其中 y (t) = LTI 的輸出

x (t) = LTI 的輸入

h (t) = LTI 的衝激響應

卷積有兩種型別：

連續卷積
離散卷積

連續卷積

$ y(t) \,\,= x (t) * h (t) $

$= \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$

(或)

$= \int_{-\infty}^{\infty} x(t - \tau) h (\tau)d\tau $

離散卷積

$y(n)\,\,= x (n) * h (n)$

$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k) $

(或)

$= \Sigma_{k = - \infty}^{\infty} x(n-k) h (k) $

透過使用卷積，我們可以找到系統的零狀態響應。

反捲積

反捲積是卷積的逆過程，廣泛應用於訊號和影像處理。

卷積的性質

交換律

$ x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t) $

分配律

$ x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$

結合律

$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t) $

移位性質

$ x_1 (t) * x_2 (t) = y (t) $

$ x_1 (t) * x_2 (t-t_0) = y (t-t_0) $

$ x_1 (t-t_0) * x_2 (t) = y (t-t_0) $

$ x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1) $

與衝激的卷積

$ x_1 (t) * \delta (t) = x(t) $

$ x_1 (t) * \delta (t- t_0) = x(t-t_0) $

單位階躍函式的卷積

$ u (t) * u (t) = r(t) $

$ u (t-T_1) * u (t-T_2) = r(t-T_1-T_2) $

$ u (n) * u (n) = [n+1] u(n) $

縮放性質

如果 $x (t) * h (t) = y (t) $

則 $x (a t) * h (a t) = {1 \over |a|} y (a t)$

輸出的微分

如果 $y (t) = x (t) * h (t)$

則 $ {dy (t) \over dt} = {dx(t) \over dt} * h (t) $

或

$ {dy (t) \over dt} = x (t) * {dh(t) \over dt}$

注意

兩個因果序列的卷積是因果的。
兩個反因果序列的卷積是反因果的。
兩個不等長矩形的卷積結果為梯形。
兩個等長矩形的卷積結果為三角形。
一個函式與其自身的卷積等於該函式的積分。

示例：您知道 $u(t) * u(t) = r(t)$

根據以上說明，$u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$

在這裡，您只需對 $u(t)$ 進行積分即可得到結果。

卷積訊號的範圍

如果兩個訊號進行卷積，則得到的卷積訊號具有以下範圍：

下限之和 < t < 上限之和

例如：求下面給出的訊號卷積的範圍

這裡，我們有兩個不等長的矩形進行卷積，結果為梯形。

卷積訊號的範圍是

下限之和 < t < 上限之和

$-1+-2 < t < 2+2 $

$-3 < t < 4 $

因此，結果是週期為 7 的梯形。

卷積訊號的面積

卷積訊號下的面積由 $A_y = A_x A_h$ 給出

其中 A_x = 輸入訊號下的面積

A_h = 衝激響應下的面積

A_y = 輸出訊號下的面積

證明： $y(t) = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$

兩邊取積分

$ \int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x (\tau) h (t-\tau)d\tau dt $

$ =\int x (\tau) d\tau \int_{-\infty}^{\infty}\, h (t-\tau) dt $

我們知道任何訊號的面積就是該訊號本身的積分。

$\therefore A_y = A_x\,A_h$

直流分量

任何訊號的直流分量由下式給出：

$\text{直流分量}={\text{訊號的面積} \over \text{訊號的週期}}$

例如：下面給出的卷積訊號的直流分量是多少？

dc component of the resultant convoluted signal

這裡 x₁(t) 的面積 = 長度 × 寬度 = 1 × 3 = 3

x₂(t) 的面積 = 長度 × 寬度 = 1 × 4 = 4

卷積訊號的面積 = x₁(t) 的面積 × x₂(t) 的面積

= 3 × 4 = 12

卷積訊號的持續時間 = 下限之和 < t < 上限之和

= -1 + -2 < t < 2+2

= -3 < t < 4

週期=7

$\therefore$ 卷積訊號的直流分量 = $\text{訊號的面積} \over \text{訊號的週期}$

直流分量 = ${12 \over 7}$

離散卷積

讓我們看看如何計算離散卷積

i. 計算離散線性卷積

對兩個序列 x[n] = {a,b,c} 和 h[n] = [e,f,g] 進行卷積

卷積輸出 = [ ea, eb+fa, ec+fb+ga, fc+gb, gc]

注意：如果兩個序列分別有 m、n 個樣本，則得到的卷積序列將有 [m+n-1] 個樣本。

示例：對兩個序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 進行卷積

卷積輸出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]

= [-1, 0, 3, 10, 6]

這裡 x[n] 包含 3 個樣本，h[n] 也包含 3 個樣本，因此得到的序列有 3+3-1 = 5 個樣本。

ii. 計算週期性或迴圈卷積

週期性卷積對離散傅立葉變換有效。要計算週期性卷積，所有樣本必須是實數。週期性或迴圈卷積也稱為快速卷積。

如果分別長度為 m、n 的兩個序列使用迴圈卷積進行卷積，則得到的序列將具有 max [m,n] 個樣本。

例如：使用迴圈卷積對兩個序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 進行卷積

正常的卷積輸出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]。

= [-1, 0, 3, 10, 6]

這裡 x[n] 包含 3 個樣本，h[n] 也包含 3 個樣本。因此，透過迴圈卷積得到的序列必須具有 max[3,3]= 3 個樣本。

現在要獲得週期性卷積結果，正常卷積的前 3 個樣本（因為週期為 3）相同，接下來的兩個樣本新增到第一個樣本中，如下所示

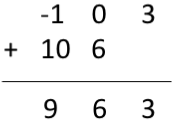
$\therefore$ 迴圈卷積結果 $y[n] = [9\quad 6\quad 3 ]$

自相關函式

它定義為訊號與其自身的相關性。自相關函式是衡量訊號與其延遲版本之間相似度的一種方法。它用 R($\tau$) 表示。

考慮一個訊號 x(t)。x(t) 與其延遲版本的自相關函式由下式給出：

$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x(t-\tau) dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + \tau) dt \quad \quad \text{[-ve shift]} $$

其中 $\tau$ = 搜尋或掃描或延遲引數。

如果訊號是複數，則自相關函式由下式給出：

$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x * (t-\tau) dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + \tau)x * (t) dt \quad \quad \text{[-ve shift]} $$

能量訊號的自相關函式的性質

自相關表現出共軛對稱性，即 R ($\tau$) = R*(-$\tau$)
能量訊號在原點（即 $\tau$=0 處）的自相關函式等於該訊號的總能量，表示為：

R (0) = E = $ \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt $
自相關函式 $\infty {1 \over \tau} $，
自相關函式在 $\tau$=0 處最大，即 |R ($\tau$) | ≤ R (0) ∀ $\tau$
自相關函式和能量譜密度是傅立葉變換對。即

$F.T\,[ R (\tau) ] = \Psi(\omega)$

$\Psi(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d \tau$
$ R (\tau) = x (\tau)* x(-\tau) $

功率訊號的自相關函式

週期為 T 的週期性功率訊號的自相關函式由下式給出：

$$ R (\tau) = \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t-\tau) dt $$

性質

功率訊號的自相關表現出共軛對稱性，即 $ R (\tau) = R*(-\tau)$
功率訊號在 $\tau = 0$（在原點）處自相關函式等於該訊號的總功率。即

$R (0)= \rho $
功率訊號的自相關函式 $\infty {1 \over \tau}$，
功率訊號的自相關函式在 $\tau$ = 0 處最大，即

$ | R (\tau) | \leq R (0)\, \forall \,\tau$
自相關函式和功率譜密度是傅立葉變換對。即

$F.T[ R (\tau) ] = s(\omega)$

$s(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d\tau$
$R (\tau) = x (\tau)* x(-\tau) $

密度譜

讓我們看看密度譜

能量密度譜

能量密度譜可以使用以下公式計算：

$$ E = \int_{-\infty}^{\infty} |\,x(f)\,|^2 df $$

功率密度譜

功率密度譜可以使用以下公式計算：

$$P = \Sigma_{n = -\infty}^{\infty}\, |\,C_n |^2 $$

互相關函式

互相關是衡量兩個不同訊號之間相似度的一種方法。

考慮兩個訊號 x₁(t) 和 x₂(t)。這兩個訊號的互相關 $R_{12}(\tau)$ 由下式給出：

$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2 (t)\, dt \quad \quad \text{[-ve shift]}$$

如果訊號是複數，則

$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$

$$R_{21} (\tau) = \int_{-\infty}^{\infty} x_2 (t)x_1^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_2 (t+\tau)x_1^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$

能量和功率訊號的互相關函式的性質

自相關表現出共軛對稱性，即 $R_{12} (\tau) = R^*_{21} (-\tau)$。
互相關不像卷積那樣滿足交換律，即

$$ R_{12} (\tau) \neq R_{21} (-\tau) $$
如果 R₁₂(0) = 0，這意味著如果 $ \int_{-\infty}^{\infty} x_1 (t) x_2^* (t) dt = 0$，則這兩個訊號被稱為正交的。

對於功率訊號，如果 $ \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x^* (t)\,dt $，則這兩個訊號被稱為正交的。
互相關函式對應於一個訊號的頻譜與另一個訊號的頻譜的複共軛的乘積。即

$$ R_{12} (\tau) \leftarrow \rightarrow X_1(\omega) X_2^*(\omega)$$

這也被稱為相關定理。

帕塞瓦爾定理

帕塞瓦爾定理對於能量訊號指出，訊號的總能量可以透過訊號的頻譜獲得，如下所示：

$ E = {1\over 2 \pi} \int_{-\infty}^{\infty} |X(\omega)|^2 d\omega $

注意：如果一個訊號的能量為E，那麼該訊號的時間尺度版本x(at)的能量為E/a。

列印頁面