
- 訊號與系統教程
- 訊號與系統首頁
- 訊號與系統概述
- 訊號基本型別
- 訊號分類
- 訊號基本運算
- 系統分類
- 訊號分析
- 傅立葉級數
- 傅立葉級數性質
- 傅立葉級數型別
- 傅立葉變換
- 傅立葉變換性質
- 無失真傳輸
- 希爾伯特變換
- 卷積與相關
- 訊號取樣定理
- 訊號取樣技術
- 拉普拉斯變換
- 拉普拉斯變換性質
- 收斂域
- Z 變換 (ZT)
- Z 變換性質
- 訊號與系統資源
- 訊號與系統 - 快速指南
- 訊號與系統 - 資源
- 訊號與系統 - 討論
訊號與系統 - 快速指南
什麼是訊號?
訊號是隨時間變化的物理現象,旨在傳遞資訊。
或
訊號是時間的函式。
或
訊號是一個或多個自變數的函式,包含一些資訊。
示例:語音訊號、影片訊號、電話線上的訊號等。
注意:噪聲也是一種訊號,但噪聲傳遞的資訊是不需要的,因此被認為是不希望的。
什麼是系統?
系統是裝置或裝置組合,可以對訊號進行操作併產生相應的響應。系統的輸入稱為激勵,輸出稱為響應。
對於一個或多個輸入,系統可以有一個或多個輸出。
示例:通訊系統

訊號基本型別
以下是一些基本訊號
單位階躍函式
單位階躍函式用 u(t) 表示。其定義為 u(t) = $\left\{\begin{matrix}1 & t \geqslant 0\\ 0 & t<0 \end{matrix}\right.$

- 它被用作最佳測試訊號。
- 單位階躍函式下的面積為單位。
單位衝激函式
衝激函式用 δ(t) 表示,其定義為 δ(t) = $\left\{\begin{matrix}1 & t = 0\\ 0 & t\neq 0 \end{matrix}\right.$

$$ \int_{-\infty}^{\infty} δ(t)dt=u (t)$$
$$ \delta(t) = {du(t) \over dt } $$
斜坡訊號
斜坡訊號用 r(t) 表示,其定義為 r(t) = $\left\{\begin {matrix}t & t\geqslant 0\\ 0 & t < 0 \end{matrix}\right. $

$$ \int u(t) = \int 1 = t = r(t) $$
$$ u(t) = {dr(t) \over dt} $$
單位斜坡下的面積為單位。
拋物線訊號
拋物線訊號可以定義為 x(t) = $\left\{\begin{matrix} t^2/2 & t \geqslant 0\\ 0 & t < 0 \end{matrix}\right.$

$$\iint u(t)dt = \int r(t)dt = \int t dt = {t^2 \over 2} = 拋物線訊號 $$
$$ \Rightarrow u(t) = {d^2x(t) \over dt^2} $$
$$ \Rightarrow r(t) = {dx(t) \over dt} $$
符號函式
符號函式用 sgn(t) 表示。其定義為 sgn(t) = $ \left\{\begin{matrix}1 & t>0\\ 0 & t=0\\ -1 & t<0 \end{matrix}\right. $

指數訊號
指數訊號的形式為 x(t) = $e^{\alpha t}$。
指數的形狀由 $\alpha$ 定義。
情況一:如果 $\alpha$ = 0 $\to$ x(t) = $e^0$ = 1

情況二:如果 $\alpha$ < 0 即 -ve 則 x(t) = $e^{-\alpha t}$。形狀稱為衰減指數。

情況三:如果 $\alpha$ > 0 即 +ve 則 x(t) = $e^{\alpha t}$。形狀稱為上升指數。

矩形訊號
設其用 x(t) 表示,其定義為

三角形訊號
設其用 x(t) 表示

正弦訊號
正弦訊號的形式為 x(t) = A cos(${w}_{0}\,\pm \phi$) 或 A sin(${w}_{0}\,\pm \phi$)

其中 T0 = $ 2\pi \over {w}_{0} $
Sinc 函式
它表示為 sinc(t),其定義為 sinc
$$ (t) = {sin \pi t \over \pi t} $$
$$ = 0\, \text{對於 t} = \pm 1, \pm 2, \pm 3 ... $$

取樣函式
它表示為 sa(t),其定義為
$$sa(t) = {sin t \over t}$$
$$= 0 \,\, \text{對於 t} = \pm \pi,\, \pm 2 \pi,\, \pm 3 \pi \,... $$

訊號分類
訊號可分為以下幾類
連續時間訊號和離散時間訊號
確定性訊號和非確定性訊號
偶訊號和奇訊號
週期訊號和非週期訊號
能量訊號和功率訊號
實訊號和虛訊號
連續時間訊號和離散時間訊號
當訊號在所有時間點都定義時,則稱該訊號為連續訊號。

當訊號僅在離散時間點定義時,則稱該訊號為離散訊號。

確定性訊號和非確定性訊號
如果在任何時間點關於其值沒有不確定性,則稱該訊號為確定性訊號。或者,可以用數學公式精確定義的訊號稱為確定性訊號。

如果在某些時間點關於其值存在不確定性,則稱該訊號為非確定性訊號。非確定性訊號本質上是隨機的,因此稱為隨機訊號。隨機訊號不能用數學方程描述。它們以機率術語建模。

偶訊號和奇訊號
如果訊號滿足條件 x(t) = x(-t),則稱該訊號為偶訊號
示例 1:t2、t4…cost 等。
設 x(t) = t2
x(-t) = (-t)2 = t2 = x(t)
$\therefore, $ t2 是偶函式
示例 2:如下圖所示,矩形函式 x(t) = x(-t),因此它也是偶函式。

如果訊號滿足條件 x(t) = -x(-t),則稱該訊號為奇訊號
示例:t、t3…和 sin t
設 x(t) = sin t
x(-t) = sin(-t) = -sin t = -x(t)
$\therefore, $ sin t 是奇函式。
任何函式 ƒ(t) 都可以表示為其偶函式 ƒe(t) 和奇函式 ƒo(t) 的和。
ƒ(t ) = ƒe(t ) + ƒ0(t )
其中
ƒe(t ) = ½[ƒ(t ) +ƒ(-t )]
週期訊號和非週期訊號
如果訊號滿足條件 x(t) = x(t + T) 或 x(n) = x(n + N),則稱該訊號為週期訊號。
其中
T = 基本週期,
1/T = f = 基本頻率。

上述訊號將在每個時間間隔 T0 重複,因此它是週期為 T0 的週期訊號。
能量訊號和功率訊號
如果訊號具有有限能量,則稱該訊號為能量訊號。
$$\text{能量}\, E = \int_{-\infty}^{\infty} x^2\,(t)dt$$
如果訊號具有有限功率,則稱該訊號為功率訊號。
$$\text{功率}\, P = \lim_{T \to \infty}\,{1\over2T}\,\int_{-T}^{T}\,x^2(t)dt$$
注意:一個訊號不可能同時是能量訊號和功率訊號。此外,訊號可能既不是能量訊號也不是功率訊號。
能量訊號的功率 = 0
功率訊號的能量 = ∞
實訊號和虛訊號
如果訊號滿足條件 x(t) = x*(t),則稱該訊號為實訊號
如果訊號滿足條件 x(t) = -x*(t),則稱該訊號為奇訊號
示例
如果 x(t)= 3 則 x*(t)=3*=3 這裡 x(t) 是實訊號。
如果 x(t)= 3j 則 x*(t)=3j* = -3j = -x(t) 因此 x(t) 是奇訊號。
注意:對於實訊號,虛部應為零。類似地,對於虛訊號,實部應為零。
訊號基本運算
一般有兩個可變引數
- 幅度
- 時間
可以使用以下運算對幅度進行運算
幅度縮放
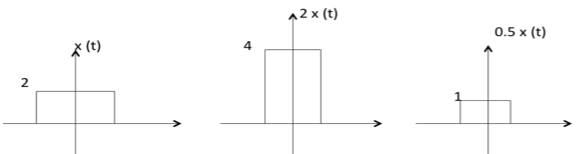
C x(t) 是 x(t) 的幅度縮放版本,其幅度按因子 C 縮放。
加法
兩個訊號的加法就是它們對應幅度的加法。這可以透過以下示例最好地解釋
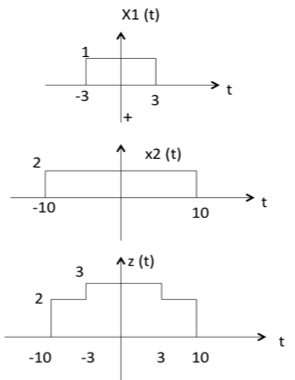
從上圖可以看出,
-10 < t < -3 z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2
-3 < t < 3 z(t) 的幅度 = x1(t) + x2(t) = 1 + 2 = 3
3 < t < 10 z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2
減法
兩個訊號的減法就是它們對應幅度的減法。這可以透過以下示例最好地解釋
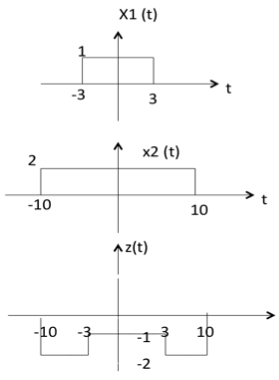
從上圖可以看出,
- -10 < t < -3 z (t) 的幅度 = x1(t) - x2(t) = 0 - 2 = -2
- -3 < t < 3 z (t) 的幅度 = x1(t) - x2(t) = 1 - 2 = -1
- 3 < t < 10 z (t) 的幅度 = x1(t) + x2(t) = 0 - 2 = -2
乘法
兩個訊號的乘法就是它們對應幅度的乘法。這可以透過以下示例最好地解釋
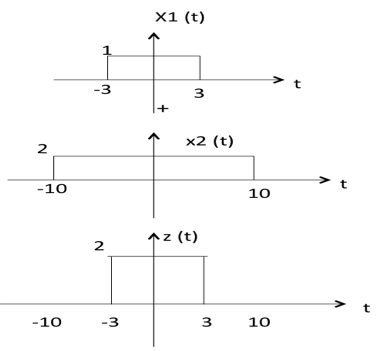
從上圖可以看出,
-10 < t < -3 z (t) 的幅度 = x1(t) ×x2(t) = 0 ×2 = 0
-3 < t < 3 z (t) 的幅度 = x1(t) ×x2(t) = 1 ×2 = 2
3 < t < 10 z (t) 的幅度 = x1(t) × x2(t) = 0 × 2 = 0
時間移位
x(t $\pm$ t0) 是訊號 x(t) 的時間移位版本。
x (t + t0) $\to$ 負移位
x (t - t0) $\to$ 正移位

時間縮放
x(At) 是訊號 x(t) 的時間縮放版本。其中 A 始終為正。
|A| > 1 $\to$ 訊號壓縮
|A| < 1 $\to$ 訊號擴充套件

注意:u(at) = u(t) 時間縮放不適用於單位階躍函式。
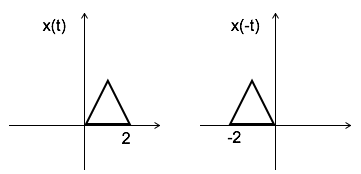
時間反轉
x(-t) 是訊號 x(t) 的時間反轉。
系統分類
系統可分為以下幾類
- 線性系統和非線性系統
- 時變系統和時不變系統
- 線性時變系統和線性時不變系統
- 靜態系統和動態系統
- 因果系統和非因果系統
- 可逆系統和不可逆系統
- 穩定系統和不穩定系統
線性系統和非線性系統
如果系統滿足疊加原理和齊次性原理,則稱該系統為線性系統。考慮兩個系統,其輸入為 x1(t)、x2(t),輸出分別為 y1(t)、y2(t)。然後,根據疊加原理和齊次性原理,
T [a1 x1(t) + a2 x2(t)] = a1 T[x1(t)] + a2 T[x2(t)]
$\therefore, $ T [a1 x1(t) + a2 x2(t)] = a1 y1(t) + a2 y2(t)
從上述表示式可以清楚地看出,整個系統的響應等於各個系統的響應。
示例
(t) = x2(t)
解決方案
y1 (t) = T[x1(t)] = x12(t)
y2 (t) = T[x2(t)] = x22(t)
T [a1 x1(t) + a2 x2(t)] = [ a1 x1(t) + a2 x2(t)]2
這與 a1 y1(t) + a2 y2(t) 不相等。因此,該系統被稱為非線性系統。
時變系統和時不變系統
如果系統的輸入和輸出特性隨時間變化,則稱該系統為時變系統。否則,該系統被認為是時不變系統。
時不變系統的條件是
y (n , t) = y(n-t)
時變系統的條件是
y (n , t) $\neq$ y(n-t)
其中 y (n , t) = T[x(n-t)] = 輸入變化
y (n-t) = 輸出變化
示例
y(n) = x(-n)
y(n, t) = T[x(n-t)] = x(-n-t)
y(n-t) = x(-(n-t)) = x(-n + t)
$\therefore$ y(n, t) ≠ y(n-t)。因此,該系統是時變系統。
線性時變 (LTV) 和線性時不變 (LTI) 系統
如果一個系統既是線性的又是時變的,則稱為線性時變 (LTV) 系統。
如果一個系統既是線性的又是時不變的,則稱為線性時不變 (LTI) 系統。
靜態系統和動態系統
靜態系統是無記憶的,而動態系統是有記憶的。
示例 1: y(t) = 2 x(t)
對於當前值 t=0,系統輸出為 y(0) = 2x(0)。這裡,輸出僅取決於當前輸入。因此,該系統是無記憶或靜態的。
示例 2: y(t) = 2 x(t) + 3 x(t-3)
對於當前值 t=0,系統輸出為 y(0) = 2x(0) + 3x(-3)。
這裡 x(-3) 是當前輸入的過去值,系統需要記憶才能得到此輸出。因此,該系統是一個動態系統。
因果系統和非因果系統
如果一個系統的輸出取決於當前和過去的輸入,而不取決於未來的輸入,則稱該系統為因果系統。
對於非因果系統,輸出也取決於未來的輸入。
示例 1: y(n) = 2 x(t) + 3 x(t-3)
對於當前值 t=1,系統輸出為 y(1) = 2x(1) + 3x(-2)。
這裡,系統輸出僅取決於當前和過去的輸入。因此,該系統是因果的。
示例 2: y(n) = 2 x(t) + 3 x(t-3) + 6x(t + 3)
對於當前值 t=1,系統輸出為 y(1) = 2x(1) + 3x(-2) + 6x(4)。這裡,系統輸出取決於未來的輸入。因此,該系統是非因果系統。
可逆系統和不可逆系統
如果系統的輸入出現在輸出端,則稱該系統為可逆的。

Y(S) = X(S) H1(S) H2(S)
= X(S) H1(S) · $1 \over ( H1(S) )$ 因為 H2(S) = 1/( H1(S) )
$\therefore, $ Y(S) = X(S)
$\to$ y(t) = x(t)
因此,該系統是可逆的。
如果 y(t) $\neq$ x(t),則稱該系統為不可逆的。
穩定系統和不穩定系統
只有當輸出對於有界輸入是有界的時,該系統才被稱為穩定。對於有界輸入,如果輸出在系統中是無界的,則稱其為不穩定。
注意:對於有界訊號,幅度是有限的。
示例 1: y (t) = x2(t)
假設輸入為 u(t)(單位階躍有界輸入),則輸出 y(t) = u2(t) = u(t) = 有界輸出。
因此,該系統是穩定的。
示例 2: y (t) = $\int x(t)\, dt$
假設輸入為 u (t)(單位階躍有界輸入),則輸出 y(t) = $\int u(t)\, dt$ = 斜坡訊號(無界,因為斜坡的幅度不是有限的,當 t $\to$ 無窮大時,它會趨於無窮大)。
因此,該系統是不穩定的。
訊號分析
向量和訊號之間的類比
向量和訊號之間存在完美的類比。
向量
向量包含大小和方向。向量的名稱用粗體表示,其大小用普通字體表示。
示例:V 是一個大小為 V 的向量。考慮以下圖中所示的兩個向量 V1 和 V2。設 V1 沿 V2 的分量由 C12V2 給出。可以透過從 V1 的末端向向量 V2 作垂線來獲得向量 V1 沿向量 V2 的分量,如圖所示

向量 V1 可以用向量 V2 表示
V1= C12V2 + Ve
其中 Ve 是誤差向量。
但這並不是用 V2 表示向量 V1 的唯一方法。替代可能性是
V1=C1V2+Ve1

V2=C2V2+Ve2

對於較大的分量值,誤差訊號最小。如果 C12=0,則兩個訊號被稱為正交。
兩個向量的點積
V1 . V2 = V1.V2 cosθ
θ = V1 和 V2 之間的角度
V1 . V2 =V2.V1
V1 沿 V2 的分量 = V1 Cos θ = $V1.V2 \over V2$
從圖中,V1 沿 V2 的分量 = C 12 V2
$$V_1.V_2 \over V_2 = C_12\,V_2$$
$$ \Rightarrow C_{12} = {V_1.V_2 \over V_2}$$
訊號
正交的概念可以應用於訊號。讓我們考慮兩個訊號 f1(t) 和 f2(t)。與向量類似,您可以用 f2(t) 來近似 f1(t),如下所示
f1(t) = C12 f2(t) + fe(t) 對於 (t1 < t < t2)
$ \Rightarrow $ fe(t) = f1(t) – C12 f2(t)
最小化誤差的一種可能方法是在區間 t1 到 t2 上進行積分。
$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)] dt$$
$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_1(t) - C_{12}f_2(t)]dt $$
但是,此步驟也不能將誤差降低到可觀的程度。這可以透過取誤差函式的平方來糾正。
$\varepsilon = {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)]^2 dt$
$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t) - C_{12}f_2]^2 dt $
其中 ε 是誤差訊號的均方值。要找到使誤差最小化的 C12 值,需要計算 ${d\varepsilon \over dC_{12} } = 0 $
$\Rightarrow {d \over dC_{12} } [ {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_1 (t) - C_{12} f_2 (t)]^2 dt]= 0 $
$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [ {d \over dC_{12} } f_{1}^2(t) - {d \over dC_{12} } 2f_1(t)C_{12}f_2(t)+ {d \over dC_{12} } f_{2}^{2} (t) C_{12}^2 ] dt =0 $
不包含 C12 項的項的導數為零。
$\Rightarrow \int_{t_1}^{t_2} - 2f_1(t) f_2(t) dt + 2C_{12}\int_{t_1}^{t_2}[f_{2}^{2} (t)]dt = 0 $
如果 $C_{12} = {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $ 分量為零,則兩個訊號被稱為正交。
將 C12 = 0 代入以獲得正交條件。
0 = $ {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $
$$ \int_{t_1}^{t_2} f_1 (t)f_2(t) dt = 0 $$
正交向量空間
一組完整的正交向量稱為正交向量空間。考慮如下所示的三維向量空間

考慮點 (X1, Y1, Z1) 處的向量 A。考慮三個單位向量 (VX, VY, VZ),分別沿 X、Y、Z 軸方向。由於這些單位向量是相互正交的,因此滿足以下條件
$$V_X. V_X= V_Y. V_Y= V_Z. V_Z = 1 $$
$$V_X. V_Y= V_Y. V_Z= V_Z. V_X = 0 $$
您可以將上述條件寫成
$$V_a . V_b = \left\{ \begin{array}{l l} 1 & \quad a = b \\ 0 & \quad a \neq b \end{array} \right. $$
向量 A 可以用其分量和單位向量表示為
$A = X_1 V_X + Y_1 V_Y + Z_1 V_Z................(1) $
此三維空間中的任何向量都可以僅用這三個單位向量表示。
如果考慮 n 維空間,則該空間中的任何向量 A 可以表示為
$ A = X_1 V_X + Y_1 V_Y + Z_1 V_Z+...+ N_1V_N.....(2) $
由於對於任何向量 A,單位向量的大小為 1
A 沿 x 軸的分量 = A.VX
A 沿 Y 軸的分量 = A.VY
A 沿 Z 軸的分量 = A.VZ
類似地,對於 n 維空間,A 沿某個 G 軸的分量
$= A.VG...............(3)$
將方程 2 代入方程 3。
$\Rightarrow CG= (X_1 V_X + Y_1 V_Y + Z_1 V_Z +...+G_1 V_G...+ N_1V_N)V_G$
$= X_1 V_X V_G + Y_1 V_Y V_G + Z_1 V_Z V_G +...+ G_1V_G V_G...+ N_1V_N V_G$
$= G_1 \,\,\,\,\, \text{因為 } V_G V_G=1$
$如果 V_G V_G \neq 1 \,\,\text{即} V_G V_G= k$
$AV_G = G_1V_G V_G= G_1K$
$G_1 = {(AV_G) \over K}$
正交訊號空間
讓我們考慮一組 n 個在區間 t1 到 t2 上相互正交的函式 x1(t)、x2(t)... xn(t)。由於這些函式彼此正交,因此任意兩個訊號 xj(t)、xk(t) 必須滿足正交條件。即
$$\int_{t_1}^{t_2} x_j(t)x_k(t)dt = 0 \,\,\, \text{其中}\, j \neq k$$
$$\text{令} \int_{t_1}^{t_2}x_{k}^{2}(t)dt = k_k $$
令一個函式 f(t),它可以透過新增沿相互正交訊號的分量來用此正交訊號空間近似,即
$\,\,\,f(t) = C_1x_1(t) + C_2x_2(t) + ... + C_nx_n(t) + f_e(t) $
$\quad\quad=\Sigma_{r=1}^{n} C_rx_r (t) $
$\,\,\,f(t) = f(t) - \Sigma_{r=1}^n C_rx_r (t) $
均方誤差 $ \varepsilon = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f_e(t)]^2 dt$
$$ = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f[t] - \sum_{r=1}^{n} C_rx_r(t) ]^2 dt $$
可以透過以下方式找到使均方誤差最小的分量
$$ {d\varepsilon \over dC_1} = {d\varepsilon \over dC_2} = ... = {d\varepsilon \over dC_k} = 0 $$
讓我們考慮 ${d\varepsilon \over dC_k} = 0 $
$${d \over dC_k}[ {1 \over t_2 - t_1} \int_{t_1}^{t_2} [ f(t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt] = 0 $$
所有不包含 Ck 的項都為零。即在求和中,r=k 項保留,所有其他項都為零。
$$\int_{t_1}^{t_2} - 2 f(t)x_k(t)dt + 2C_k \int_{t_1}^{t_2} [x_k^2 (t)] dt=0 $$
$$\Rightarrow C_k = {{\int_{t_1}^{t_2}f(t)x_k(t)dt} \over {int_{t_1}^{t_2} x_k^2 (t)dt}} $$
$$\Rightarrow \int_{t_1}^{t_2} f(t)x_k(t)dt = C_kK_k $$
均方誤差
誤差函式 fe(t) 平方值的平均值稱為均方誤差。它用 ε(epsilon)表示。
.$\varepsilon = {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t)]^2dt$
$\,\,\,\,= {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt $
$\,\,\,\,= {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f_e^2 (t) ]dt + \Sigma_{r=1}^{n} C_r^2 \int_{t_1}^{t_2} x_r^2 (t) dt - 2 \Sigma_{r=1}^{n} C_r \int_{t_1}^{t_2} x_r (t)f(t)dt$
已知 $C_{r}^{2} \int_{t_1}^{t_2} x_r^2 (t)dt = C_r \int_{t_1}^{t_2} x_r (t)f(d)dt = C_r^2 K_r $
$\varepsilon = {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f^2 (t)] dt + \Sigma_{r=1}^{n} C_r^2 K_r - 2 \Sigma_{r=1}^{n} C_r^2 K_r] $
$\,\,\,\,= {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt - \Sigma_{r=1}^{n} C_r^2 K_r ] $
$\, \therefore \varepsilon = {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt + (C_1^2 K_1 + C_2^2 K_2 + ... + C_n^2 K_n)] $
上述公式用於評估均方誤差。
正交函式的閉集和完備集
考慮一組在區間 t1 到 t2 上互為正交的 n 個函式 x1(t),x2(t)...xn(t)。當不存在任何滿足條件 $\int_{t_1}^{t_2} f(t)x_k(t)dt = 0 $ 的函式 f(t) 時,這組函式被稱為閉集和完備集。
如果該函式滿足方程 $\int_{t_1}^{t_2} f(t)x_k(t)dt=0 \,\, \text{for}\, k = 1,2,..$,則稱 f(t) 與正交集中的每個函式都正交。如果沒有 f(t),則該集合是不完備的。當包含 f(t) 時,它就變成了閉集和完備集。
可以透過沿著互為正交的訊號新增分量,用這組正交集近似 f(t),即
$$f(t) = C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t) + f_e(t) $$
如果無限級數 $C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t)$ 收斂於 f(t),則均方誤差為零。
複函式的正交性
如果 f1(t) 和 f2(t) 是兩個複函式,則 f1(t) 可以用 f2(t) 表示為
$f_1(t) = C_{12}f_2(t) \,\,\,\,\,\,\,\,$ ..誤差可忽略不計
其中 $C_{12} = {{\int_{t_1}^{t_2} f_1(t)f_2^*(t)dt} \over { \int_{t_1}^{t_2} |f_2(t)|^2 dt}} $
其中 $f_2^* (t)$ = f2(t) 的共軛複數。
如果 f1(t) 和 f2(t) 正交,則 C12 = 0
$$ {\int_{t_1}^{t_2} f_1 (t) f_2^*(t) dt \over \int_{t_1}^{t_2} |f_2 (t) |^2 dt} = 0 $$
$$\Rightarrow \int_{t_1}^{t_2} f_1 (t) f_2^* (dt) = 0$$
上述公式表示複函式的正交性條件。
傅立葉級數
**傅立葉 (Jean Baptiste Joseph Fourier)**,法國數學家和物理學家;出生於法國歐塞爾。他創立了傅立葉級數、傅立葉變換及其在熱傳遞和振動問題中的應用。傅立葉級數、傅立葉變換和傅立葉定律都是以他的名字命名的。

傅立葉級數
為了表示任何週期訊號 x(t),傅立葉發展了一個稱為傅立葉級數的表示式。它用正弦和餘弦或指數的無限和表示。傅立葉級數利用了正交性條件。
連續時間週期訊號的傅立葉級數表示
如果訊號滿足條件 x (t) = x (t + T) 或 x (n) = x (n + N),則稱該訊號為週期訊號。
其中 T = 基本週期,
ω0= 基本頻率 = 2π/T
有兩種基本週期訊號
$x(t) = \cos\omega_0t$ (正弦波) &
$x(t) = e^{j\omega_0 t} $ (復指數)
這兩種訊號的週期為 $T= 2\pi/\omega_0$。
一組諧波相關的復指數可以表示為 {$\phi_k (t)$}
$${ \phi_k (t)} = \{ e^{jk\omega_0t}\} = \{ e^{jk({2\pi \over T})t}\} \text{其中} \,k = 0 \pm 1, \pm 2 ..n \,\,\,.....(1) $$
所有這些訊號的週期都是 T
根據正交訊號空間,用 n 個互為正交的函式逼近函式 x (t) 的公式為
$$x(t) = \sum_{k = - \infty}^{\infty} a_k e^{jk\omega_0t} ..... (2) $$
$$ = \sum_{k = - \infty}^{\infty} a_kk e^{jk\omega_0t} $$
其中 $a_k$= 傅立葉係數 = 逼近係數。
該訊號 x(t) 的週期也為 T。
公式 (2) 表示週期訊號 x(t) 的傅立葉級數表示。
k = 0 項為常數項。
k = ±1 項具有基本頻率 ω0,稱為一次諧波。
k = ±2 項具有基本頻率 2ω0,稱為二次諧波,以此類推…
k = ±n 項具有基本頻率 nω0,稱為 n 次諧波。
推導傅立葉係數
已知 $x(t) = \Sigma_{k=- \infty}^{\infty} a_k e^{jk \omega_0 t} ...... (1)$
兩邊乘以 $e^{-jn\omega_0 t}$。然後
$$ x(t)e^{-jn\omega_0 t} = \sum_{k=- \infty}^{\infty} a_k e^{jk \omega_0 t} . e^{-jn\omega_0 t} $$
考慮兩邊的積分。
$$ \int_{0}^{T} x(t) e^{jk \omega_0 t} dt = \int_{0}^{T} \sum_{k=-\infty}^{\infty} a_k e^{jk \omega_0 t} . e^{-jn\omega_0 t}dt $$
$$ \quad \quad \quad \quad \,\, = \int_{0}^{T} \sum_{k=-\infty}^{\infty} a_k e^{j(k-n) \omega_0 t} . dt$$
$$ \int_{0}^{T} x(t) e^{jk \omega_0 t} dt = \sum_{k=-\infty}^{\infty} a_k \int_{0}^{T} e^{j(k-n) \omega_0 t} dt. \,\, ..... (2)$$
根據尤拉公式,
$$ \int_{0}^{T} e^{j(k-n) \omega_0 t} dt. = \int_{0}^{T} \cos(k-n)\omega_0 dt + j \int_{0}^{T} \sin(k-n)\omega_0t\,dt$$
$$ \int_{0}^{T} e^{j(k-n) \omega_0 t} dt. = \left\{ \begin{array}{l l} T & \quad k = n \\ 0 & \quad k \neq n \end{array} \right. $$
因此,在公式 (2) 中,除了 k = n 時,積分對所有 k 值都為零。在公式 (2) 中令 k = n。
$$\Rightarrow \int_{0}^{T} x(t) e^{-jn\omega_0 t} dt = a_n T $$
$$\Rightarrow a_n = {1 \over T} \int_{0}^{T} e^{-jn\omega_0 t} dt $$
將 n 替換為 k。
$$\Rightarrow a_k = {1 \over T} \int_{0}^{T} e^{-jk\omega_0 t} dt$$
$$\therefore x(t) = \sum_{k=-\infty}^{\infty} a_k e^{j(k-n) \omega_0 t} $$
$$\text{其中} a_k = {1 \over T} \int_{0}^{T} e^{-jk\omega_0 t} dt $$
傅立葉級數性質
這些是傅立葉級數的性質
線性性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$ & $ y(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{yn}$
則線性性質表明
$ \text{a}\, x(t) + \text{b}\, y(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} \text{a}\, f_{xn} + \text{b}\, f_{yn}$
時移性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則時移性質表明
$x(t-t_0) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} e^{-jn\omega_0 t_0}f_{xn} $
頻移性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則頻移性質表明
$e^{jn\omega_0 t_0} . x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{x(n-n_0)} $
時間反轉性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則時間反轉性質表明
如果 $ x(-t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{-xn}$
時間縮放性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則時間縮放性質表明
如果 $ x(at) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
時間縮放性質將頻率分量從 ω0 更改為 aω0。
微分和積分性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則微分性質表明
如果 $ {dx(t)\over dt} \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} jn\omega_0 . f_{xn}$
& 積分性質表明
如果 $ \int x(t) dt \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} {f_{xn} \over jn\omega_0} $
乘法和卷積性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$ & $ y(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{yn}$
則乘法性質表明
$ x(t) . y(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} T f_{xn} * f_{yn}$
& 卷積性質表明
$ x(t) * y(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} T f_{xn} . f_{yn}$
共軛和共軛對稱性質
如果 $ x(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f_{xn}$
則共軛性質表明
$ x*(t) \xleftarrow[\,]{傅立葉級數\,}\xrightarrow[\,]{係數} f*_{xn}$
實值時間訊號的共軛對稱性質表明
$$f*_{xn} = f_{-xn}$$
& 虛值時間訊號的共軛對稱性質表明
$$f*_{xn} = -f_{-xn} $$
傅立葉級數型別
三角傅立葉級數 (TFS)
sin nω0 t 和 sin mω0 t 在區間 (t0, t0+{2π \over ω0}) 上正交。因此,sinω0 t、sin 2ω0 t 構成一個正交集。如果沒有 {cos nω0 t},則該集合不完備,因為該餘弦集也與正弦集正交。因此,為了使該集合完備,我們必須同時包含餘弦項和正弦項。現在,完備的正交集包含所有餘弦項和正弦項,即 {sin nω0 t、cos nω0 t},其中 n=0, 1, 2...
$\therefore$ 區間 (t0, t0+{2π \over ω0}) 中的任何函式 x(t) 可以表示為
$$ x(t) = a_0 \cos0\omega_0 t+ a_1 \cos 1\omega_0 t+ a_2 \cos2 \omega_0 t +...+ a_n \cos n\omega_0 t + ... $$
$$ + b_0 \sin 0\omega_0 t + b_1 \sin 1\omega_0 t +...+ b_n \sin n\omega_0 t + ... $$
$$ = a_0 + a_1 \cos 1\omega_0 t + a_2 \cos 2 \omega_0 t +...+ a_n \cos n\omega_0 t + ...$$
$$ + b_1 \sin 1\omega_0 t +...+ b_n \sin n\omega_0 t + ...$$
$$ \therefore x(t) = a_0 + \sum_{n=1}^{\infty} (a_n \cos n\omega_0 t + b_n \sin n\omega_0 t ) \quad (t_0< t < t_0+T)$$
上述公式表示 x(t) 的三角傅立葉級數表示。
$$\text{其中} \,a_0 = {\int_{t_0}^{t_0+T} x(t)·1 dt \over \int_{t_0}^{t_0+T} 1^2 dt} = {1 \over T}· \int_{t_0}^{t_0+T} x(t)dt $$
$$a_n = {\int_{t_0}^{t_0+T} x(t)· \cos n\omega_0 t\,dt \over \int_{t_0}^{t_0+T} \cos ^2 n\omega_0 t\, dt}$$
$$b_n = {\int_{t_0}^{t_0+T} x(t)· \sin n\omega_0 t\,dt \over \int_{t_0}^{t_0+T} \sin ^2 n\omega_0 t\, dt}$$
$$\text{這裡}\, \int_{t_0}^{t_0+T} \cos ^2 n\omega_0 t\, dt = \int_{t_0}^{t_0+T} \sin ^2 n\omega_0 t\, dt = {T\over 2}$$
$$\therefore a_n = {2\over T}· \int_{t_0}^{t_0+T} x(t)· \cos n\omega_0 t\,dt$$
$$b_n = {2\over T}· \int_{t_0}^{t_0+T} x(t)· \sin n\omega_0 t\,dt$$
指數傅立葉級數 (EFS)
考慮一組復指數函式 $\left\{e^{jn\omega_0 t}\right\} (n=0, \pm1, \pm2...)$,它在區間 $(t_0, t_0+T)$ 上是正交的。其中 $T={2\pi \over \omega_0}$。這是一個完備集,因此可以用它來表示任何函式 f(t),如下所示
$ f(t) = F_0 + F_1e^{j\omega_0 t} + F_2e^{j 2\omega_0 t} + ... + F_n e^{j n\omega_0 t} + ...$
$\quad \quad \,\,F_{-1}e^{-j\omega_0 t} + F_{-2}e^{-j 2\omega_0 t} +...+ F_{-n}e^{-j n\omega_0 t}+...$
$$ \therefore f(t) = \sum_{n=-\infty}^{\infty} F_n e^{j n\omega_0 t} \quad \quad (t_0< t < t_0+T) ....... (1) $$
公式1表示訊號 f(t) 在區間 (t0, t0+T) 上的指數傅立葉級數表示。傅立葉係數計算如下:
$$ F_n = {\int_{t_0}^{t_0+T} f(t) (e^{j n\omega_0 t} )^* dt \over \int_{t_0}^{t_0+T} e^{j n\omega_0 t} (e^{j n\omega_0 t} )^* dt} $$
$$ \quad = {\int_{t_0}^{t_0+T} f(t) e^{-j n\omega_0 t} dt \over \int_{t_0}^{t_0+T} e^{-j n\omega_0 t} e^{j n\omega_0 t} dt} $$
$$ \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, = {\int_{t_0}^{t_0+T} f(t) e^{-j n\omega_0 t} dt \over \int_{t_0}^{t_0+T} 1\, dt} = {1 \over T} \int_{t_0}^{t_0+T} f(t) e^{-j n\omega_0 t} dt $$
$$ \therefore F_n = {1 \over T} \int_{t_0}^{t_0+T} f(t) e^{-j n\omega_0 t} dt $$
三角傅立葉級數與指數傅立葉級數之間的關係
考慮一個週期訊號 x(t),其TFS和EFS表示分別如下所示
$ x(t) = a_0 + \Sigma_{n=1}^{\infty}(a_n \cos n\omega_0 t + b_n \sin n\omega_0 t) ... ... (1)$
$ x(t) = \Sigma_{n=-\infty}^{\infty} F_n e^{j n\omega_0 t}$
$\quad \,\,\, = F_0 + F_1e^{j\omega_0 t} + F_2e^{j 2\omega_0 t} + ... + F_n e^{j n\omega_0 t} + ... $
$\quad \quad \quad \quad F_{-1} e^{-j\omega_0 t} + F_{-2}e^{-j 2\omega_0 t} + ... + F_{-n}e^{-j n\omega_0 t} + ... $
$ = F_0 + F_1(\cos \omega_0 t + j \sin\omega_0 t) + F_2(cos 2\omega_0 t + j \sin 2\omega_0 t) + ... + F_n(\cos n\omega_0 t+j \sin n\omega_0 t)+ ... + F_{-1}(\cos\omega_0 t-j \sin\omega_0 t) + F_{-2}(\cos 2\omega_0 t-j \sin 2\omega_0 t) + ... + F_{-n}(\cos n\omega_0 t-j \sin n\omega_0 t) + ... $
$ = F_0 + (F_1+ F_{-1}) \cos\omega_0 t + (F_2+ F_{-2}) \cos2\omega_0 t +...+ j(F_1 - F_{-1}) \sin\omega_0 t + j(F_2 - F_{-2}) \sin2\omega_0 t+... $
$ \therefore x(t) = F_0 + \Sigma_{n=1}^{\infty}( (F_n +F_{-n} ) \cos n\omega_0 t+j(F_n-F_{-n}) \sin n\omega_0 t) ... ... (2) $
比較公式1和2。
$a_0= F_0$
$a_n=F_n+F_{-n}$
$b_n = j(F_n-F_{-n} )$
類似地,
$F_n = \frac12 (a_n - jb_n )$
$F_{-n} = \frac12 (a_n + jb_n )$
傅立葉變換
傅立葉級數的主要缺點是,它只適用於週期訊號。有一些自然產生的訊號,例如非週期性或非週期性訊號,我們無法使用傅立葉級數來表示。為了克服這個缺點,傅立葉開發了一個數學模型,用於在時域(或空間域)和頻域之間轉換訊號,反之亦然,這被稱為“傅立葉變換”。
傅立葉變換在物理學和工程學中有很多應用,例如線性時不變系統的分析、雷達、天文學、訊號處理等。
從傅立葉級數推導傅立葉變換
考慮一個週期為T的週期訊號 f(t)。f(t) 的復傅立葉級數表示為
$$ f(t) = \sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0 t} $$
$$ \quad \quad \quad \quad \quad = \sum_{k=-\infty}^{\infty} a_k e^{j {2\pi \over T_0} kt} ... ... (1) $$
令 ${1 \over T_0} = \Delta f$,則公式1變為
$f(t) = \sum_{k=-\infty}^{\infty} a_k e^{j2\pi k \Delta ft} ... ... (2) $
但你知道
$a_k = {1\over T_0} \int_{t_0}^{t_0+T} f(t) e^{-j k\omega_0 t} dt$
代入公式2。
(2) $ \Rightarrow f(t) = \Sigma_{k=-\infty}^{\infty} {1 \over T_0} \int_{t_0}^{t_0+T} f(t) e^{-j k\omega_0 t} dt\, e^{j2\pi k \Delta ft} $
令 $t_0={T\over2}$
$ = \Sigma_{k=-\infty}^{\infty} [ \int_{-T\over2}^{T\over2} f(t) e^{-j2 \pi k \Delta ft} dt ] \, e^{j2 \pi k \Delta ft}.\Delta f $
當 $T \to \infty$ 時,$\Delta f$ 接近微分 $df$,$k \Delta f$ 變成連續變數 $f$,求和變成積分
$$ f(t) = lim_{T \to \infty} \left\{ \Sigma_{k=-\infty}^{\infty} [ \int_{-T\over2}^{T\over2} f(t) e^{-j2 \pi k \Delta ft} dt ] \, e^{j2 \pi k \Delta ft}.\Delta f \right\} $$
$$ = \int_{-\infty}^{\infty} [ \int_{-\infty}^{\infty}\,f(t) e^{-j2\pi ft} dt] e^{j2\pi ft} df $$
$$f(t) = \int_{-\infty}^{\infty}\, F[\omega] e^{j\omega t} d \omega$$
$\text{其中}\,F[\omega] = [ \int_{-\infty}^{\infty}\, f(t) e^{-j2 \pi ft} dt]$
訊號的傅立葉變換 $$f(t) = F[\omega] = [\int_{-\infty}^{\infty}\, f(t) e^{-j\omega t} dt]$$
傅立葉逆變換為 $$f(t) = \int_{-\infty}^{\infty}\,F[\omega] e^{j\omega t} d \omega$$
基本函式的傅立葉變換
讓我們瞭解一下基本函式的傅立葉變換
門函式的傅立葉變換

$$F[\omega] = AT Sa({\omega T \over 2})$$
衝激函式的傅立葉變換
$FT [\omega(t) ] = [\int_{- \infty}^{\infty} \delta (t) e^{-j\omega t} dt] $
$\quad \quad \quad \quad = e^{-j\omega t}\, |\, t = 0 $
$\quad \quad \quad \quad = e^{0} = 1 $
$\quad \therefore \delta (\omega) = 1 $
單位階躍函式的傅立葉變換
$U(\omega) = \pi \delta (\omega)+1/j\omega$
指數函式的傅立葉變換
$ e^{-at}u(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} 1/(a+jω)$
$ e^{-at}u(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} 1/(a+j\omega )$
$ e^{-a\,|\,t\,|} \stackrel{\mathrm{F.T}}{\longleftrightarrow} {2a \over {a^2+ω^2}}$
$ e^{j \omega_0 t} \stackrel{\mathrm{F.T}}{\longleftrightarrow} \delta (\omega - \omega_0)$
符號函式的傅立葉變換
$ sgn(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} {2 \over j \omega }$
傅立葉變換存在的條件
只有當函式滿足狄利克雷條件時,任何函式 f(t) 才能用傅立葉變換表示。即
函式 f(t) 具有有限個最大值和最小值。
在給定的時間間隔內,訊號 f(t) 必須具有有限個不連續點。
它在給定的時間間隔內必須是絕對可積的,即
$ \int_{-\infty}^{\infty}\, |\, f(t) | \, dt < \infty $
離散時間傅立葉變換 (DTFT)
離散時間傅立葉變換 (DTFT) 或離散時間序列 x[n] 的傅立葉變換是根據復指數序列 $e^{j\omega n}$ 對序列的表示。
DTFT 序列 x[n] 由下式給出
$$ X(\omega) = \Sigma_{n= -\infty}^{\infty} x(n)e^{-j \omega n} \,\, ...\,... (1) $$
這裡,X(ω) 是實頻率變數 ω 的複函式,可以寫成
$$ X(\omega) = X_{re}(\omega) + jX_{img}(\omega) $$
其中 Xre(ω),Ximg(ω) 分別是 X(ω) 的實部和虛部。
$$ X_{re}(\omega) = |\, X(\omega) | \cos\theta(\omega) $$
$$ X_{img}(\omega) = |\, X(\omega) | \sin\theta(\omega) $$
$$ |X(\omega) |^2 = |\, X_{re} (\omega) |^2+ |\,X_{im} (\omega) |^2 $$
並且 X(ω) 也可以表示為 $ X(\omega) = |\,X(\omega) | e^{j\theta (ω)} $
其中 $\theta(\omega) = arg{X(\omega) } $
$|\,X(\omega) |, \theta(\omega)$ 分別稱為 X(ω) 的幅度譜和相位譜。
離散時間傅立葉逆變換
$$ x(n) = { 1 \over 2\pi} \int_{-\pi}^{\pi} X(\omega) e^{j \omega n} d\omega \,\, ...\,... (2)$$
收斂條件
公式1中的無限級數可能收斂也可能不收斂。x(n) 是絕對可和的。
$$ \text{當}\,\, \sum_{n=-\infty}^{\infty} |\, x(n)|\, < \infty $$
絕對可和序列總是具有有限能量,但有限能量序列不一定是絕對可和的。
傅立葉變換性質
以下是傅立葉變換的性質
線性性質
$\text{如果}\,\,x (t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega) $
$ \text{&} \,\, y(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} Y(\omega) $
則線性性質指出
$a x (t) + b y (t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} a X(\omega) + b Y(\omega) $
時移性質
$\text{如果}\, x(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X (\omega)$
則時移性質指出
$x (t-t_0) \stackrel{\mathrm{F.T}}{\longleftrightarrow} e^{-j\omega t_0 } X(\omega)$
頻移性質
$\text{如果}\,\, x(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega)$
則頻移性質指出
$e^{j\omega_0 t} . x (t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega - \omega_0)$
時間反轉性質
$ \text{如果}\,\, x(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega)$
則時間反轉性質指出
$ x (-t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(-\omega)$
時間縮放性質
$ \text{如果}\,\, x (t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega) $
則時間尺度變換性質指出
$ x (at) {1 \over |\,a\,|} X { \omega \over a}$
微分和積分性質
$ If \,\, x (t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega)$
則微分性質指出
$ {dx (t) \over dt} \stackrel{\mathrm{F.T}}{\longleftrightarrow} j\omega . X(\omega)$
$ {d^n x (t) \over dt^n } \stackrel{\mathrm{F.T}}{\longleftrightarrow} (j \omega)^n . X(\omega) $
積分性質指出
$ \int x(t) \, dt \stackrel{\mathrm{F.T}}{\longleftrightarrow} {1 \over j \omega} X(\omega) $
$ \iiint ... \int x(t)\, dt \stackrel{\mathrm{F.T}}{\longleftrightarrow} { 1 \over (j\omega)^n} X(\omega) $
乘法和卷積性質
$ \text{如果} \,\, x(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega) $
$ \text{&} \,\,y(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} Y(\omega) $
則乘法性質指出
$ x(t). y(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} X(\omega)*Y(\omega) $
卷積性質指出
$ x(t) * y(t) \stackrel{\mathrm{F.T}}{\longleftrightarrow} {1 \over 2 \pi} X(\omega).Y(\omega) $
無失真傳輸
如果輸入和輸出具有相同的波形,則傳輸被稱為無失真傳輸。即,在無失真傳輸中,輸入 x(t) 和輸出 y(t) 滿足以下條件
y (t) = Kx(t - td)
其中 td = 延遲時間,
k = 常數。
對兩邊進行傅立葉變換
FT[ y (t)] = FT[Kx(t - td)]
= K FT[x(t - td)]
根據時移性質,
= KX(w)$e^{-j \omega t_d}$
$ \therefore Y(w) = KX(w)e^{-j \omega t_d}$
因此,當且僅當具有衝激響應 h(t) 的系統的輸入訊號 x(t) 的傳輸滿足以下條件時,才能實現無失真傳輸
$|H(\omega)| = K \,\, 且 \,\,\, $ (幅頻響應)
$ \Phi (\omega) = -\omega t_d = -2\pi f t_d \,\,\, $ (相頻響應)

物理傳輸系統可能具有如下所示的幅頻和相頻響應

希爾伯特變換
訊號 x(t) 的希爾伯特變換定義為將訊號所有分量的相位角移位 ±90° 的變換。
x(t) 的希爾伯特變換用 $\hat{x}(t)$ 表示,其公式為
$$ \hat{x}(t) = { 1 \over \pi } \int_{-\infty}^{\infty} {x(k) \over t-k } dk $$
希爾伯特逆變換的公式為
$$ \hat{x}(t) = { 1 \over \pi } \int_{-\infty}^{\infty} {x(k) \over t-k } dk $$
x(t),$\hat{x}$(t) 稱為希爾伯特變換對。
希爾伯特變換的性質
訊號 x(t) 及其希爾伯特變換 $\hat{x}$(t) 具有:
相同的幅度譜。
相同的自相關函式。
x(t) 和 $\hat{x}$(t) 的能量譜密度相同。
x(t) 和 $\hat{x}$(t) 正交。
$\hat{x}$(t) 的希爾伯特變換為 -x(t)
如果存在傅立葉變換,則能量和功率訊號也存在希爾伯特變換。
卷積與相關
卷積
卷積是一種數學運算,用於表達線性時不變系統輸入和輸出之間的關係。它將線性時不變系統的輸入、輸出和衝激響應聯絡起來,如下所示:
$$ y (t) = x(t) * h(t) $$
其中 y (t) = 線性時不變系統的輸出
x (t) = 線性時不變系統的輸入
h (t) = 線性時不變系統的衝激響應
卷積有兩種型別:
連續卷積
離散卷積
連續卷積

$ y(t) \,\,= x (t) * h (t) $
$= \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$
(或)
$= \int_{-\infty}^{\infty} x(t - \tau) h (\tau)d\tau $
離散卷積

$y(n)\,\,= x (n) * h (n)$
$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k) $
(或)
$= \Sigma_{k = - \infty}^{\infty} x(n-k) h (k) $
利用卷積可以求出系統的零狀態響應。
解卷積
解卷積是卷積的逆過程,廣泛應用於訊號和影像處理。
卷積的性質
交換律
$ x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t) $
分配律
$ x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$
結合律
$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t) $
移位特性
$ x_1 (t) * x_2 (t) = y (t) $
$ x_1 (t) * x_2 (t-t_0) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t) = y (t-t_0) $
$ x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1) $
與衝激的卷積
$ x_1 (t) * \delta (t) = x(t) $
$ x_1 (t) * \delta (t- t_0) = x(t-t_0) $
單位階躍函式的卷積
$ u (t) * u (t) = r(t) $
$ u (t-T_1) * u (t-T_2) = r(t-T_1-T_2) $
$ u (n) * u (n) = [n+1] u(n) $
尺度特性
如果 $x (t) * h (t) = y (t) $
則 $x (a t) * h (a t) = {1 \over |a|} y (a t)$
輸出的微分
如果 $y (t) = x (t) * h (t)$
則 $ {dy (t) \over dt} = {dx(t) \over dt} * h (t) $
或
$ {dy (t) \over dt} = x (t) * {dh(t) \over dt}$
注意
兩個因果序列的卷積是因果的。
兩個反因果序列的卷積是反因果的。
兩個不等長矩形的卷積結果為梯形。
兩個等長矩形的卷積結果為三角形。
一個函式與其自身的卷積等於該函式的積分。
示例:已知 $u(t) * u(t) = r(t)$
根據以上說明,$u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$
這裡,你只需對 $u(t)$ 進行積分即可得到結果。
卷積訊號的範圍
如果兩個訊號進行卷積,則得到的卷積訊號具有以下範圍:
下限之和 < t < 上限之和
例如:求下面給定訊號的卷積範圍

這裡,我們有兩個不等長的矩形進行卷積,結果為梯形。
卷積訊號的範圍為
下限之和 < t < 上限之和
$-1+-2 < t < 2+2 $
$-3 < t < 4 $
因此,結果是週期為 7 的梯形。
卷積訊號的面積
卷積訊號下的面積由 $A_y = A_x A_h$ 給出
其中 Ax = 輸入訊號下的面積
Ah = 衝激響應下的面積
Ay = 輸出訊號下的面積
證明: $y(t) = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$
兩邊取積分
$ \int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x (\tau) h (t-\tau)d\tau dt $
$ =\int x (\tau) d\tau \int_{-\infty}^{\infty}\, h (t-\tau) dt $
我們知道任何訊號的面積就是該訊號本身的積分。
$\therefore A_y = A_x\,A_h$
直流分量
任何訊號的直流分量由下式給出:
$\text{直流分量}={\text{訊號的面積} \over \text{訊號的週期}}$
例如:下面給出的卷積訊號的直流分量是多少?

這裡 x1(t) 的面積 = 長度 × 寬度 = 1 × 3 = 3
x2(t) 的面積 = 長度 × 寬度 = 1 × 4 = 4
卷積訊號的面積 = x1(t) 的面積 × x2(t) 的面積
= 3 × 4 = 12
卷積訊號的持續時間 = 下限之和 < t < 上限之和
= -1 + -2 < t < 2+2
= -3 < t < 4
週期=7
$\therefore$ 卷積訊號的直流分量 = $\text{訊號的面積} \over \text{訊號的週期}$
直流分量 = ${12 \over 7}$
離散卷積
讓我們看看如何計算離散卷積
i. 計算離散線性卷積
將兩個序列 x[n] = {a,b,c} 和 h[n] = [e,f,g] 進行卷積

卷積輸出 = [ ea, eb+fa, ec+fb+ga, fc+gb, gc]
注意:如果兩個序列分別有 m、n 個樣本,則得到的卷積序列將有 [m+n-1] 個樣本。
示例:將兩個序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 進行卷積

卷積輸出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]
= [-1, 0, 3, 10, 6]
這裡 x[n] 包含 3 個樣本,h[n] 也包含 3 個樣本,因此得到的序列包含 3+3-1 = 5 個樣本。
ii. 計算週期性或迴圈卷積
週期性卷積對離散傅立葉變換有效。要計算週期性卷積,所有樣本都必須是實數。週期性或迴圈卷積也稱為快速卷積。
如果兩個長度分別為 m、n 的序列使用迴圈卷積進行卷積,則得到的序列將具有 max [m,n] 個樣本。
例如:使用迴圈卷積將兩個序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 進行卷積

普通卷積輸出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]。
= [-1, 0, 3, 10, 6]
這裡 x[n] 包含 3 個樣本,h[n] 也包含 3 個樣本。因此,透過迴圈卷積得到的序列必須具有 max[3,3]= 3 個樣本。
現在要獲得週期性卷積結果,普通卷積的前 3 個樣本(因為週期為 3)相同,接下來的兩個樣本新增到第一個樣本中,如下所示
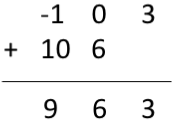
$\therefore$ 迴圈卷積結果 $y[n] = [9\quad 6\quad 3 ]$
相關性
相關性是衡量兩個訊號之間相似性的指標。相關性的通用公式為
$$ \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau) dt $$
相關性有兩種型別:
自相關
互相關
自相關函式
它被定義為訊號與其自身的相關性。自相關函式是衡量訊號與其延遲版本之間相似性的指標。它用 R($\tau$) 表示。
考慮一個訊號 x(t)。x(t) 及其延遲版本的自相關函式由下式給出:
$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x(t-\tau) dt \quad \quad \text{[正移]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + \tau) dt \quad \quad \text{[-負移]} $$
其中 $\tau$ = 搜尋或掃描或延遲引數。
如果訊號是複數,則自相關函式由下式給出:
$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x * (t-\tau) dt \quad \quad \text{[正移]} $$
$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + \tau)x * (t) dt \quad \quad \text{[-負移]} $$
能量訊號的自相關函式的性質
自相關表現出共軛對稱性,即 R ($\tau$) = R*(-$\tau$)
能量訊號在原點(即 $\tau$=0 處)的自相關函式等於該訊號的總能量,其公式為:
R (0) = E = $ \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt $
自相關函式 $\infty {1 \over \tau} $,
自相關函式在 $\tau$=0 處最大,即 |R ($\tau$) | ≤ R (0) ∀ $\tau$
自相關函式和能量譜密度是傅立葉變換對。即
$F.T\,[ R (\tau) ] = \Psi(\omega)$
$\Psi(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d \tau$
$ R (\tau) = x (\tau)* x(-\tau) $
功率訊號的自相關函式
週期為 T 的週期性功率訊號的自相關函式由下式給出:
$$ R (\tau) = \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t-\tau) dt $$
性質
功率訊號的自相關表現出共軛對稱性,即 $ R (\tau) = R*(-\tau)$
功率訊號在 $\tau = 0$(在原點)處的自相關函式等於該訊號的總功率。即
$R (0)= \rho $
功率訊號的自相關函式 $\infty {1 \over \tau}$,
功率訊號的自相關函式在 $\tau$ = 0 處最大,即
$ | R (\tau) | \leq R (0)\, \forall \,\tau$
自相關函式和功率譜密度是傅立葉變換對。即
$F.T[ R (\tau) ] = s(\omega)$
$s(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d\tau$
$R (\tau) = x (\tau)* x(-\tau) $
密度譜
讓我們看看密度譜
能量密度譜
能量密度譜可以使用以下公式計算:
$$ E = \int_{-\infty}^{\infty} |\,x(f)\,|^2 df $$
功率密度譜
功率密度譜可以使用以下公式計算:
$$P = \Sigma_{n = -\infty}^{\infty}\, |\,C_n |^2 $$
互相關函式
互相關是衡量兩個不同訊號之間相似性的指標。
考慮兩個訊號 x1(t) 和 x2(t)。這兩個訊號的互相關 $R_{12}(\tau)$ 由下式給出
$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau)\, dt \quad \quad \text{[正向移位]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2 (t)\, dt \quad \quad \text{[-向移位]}$$
如果訊號是複數,則
$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2^{*}(t-\tau)\, dt \quad \quad \text{[正向移位]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2^{*} (t)\, dt \quad \quad \text{[-向移位]}$$
$$R_{21} (\tau) = \int_{-\infty}^{\infty} x_2 (t)x_1^{*}(t-\tau)\, dt \quad \quad \text{[正向移位]} $$
$$\quad \quad = \int_{-\infty}^{\infty} x_2 (t+\tau)x_1^{*} (t)\, dt \quad \quad \text{[-向移位]}$$
能量和功率訊號的互相關函式性質
自相關具有共軛對稱性,即 $R_{12} (\tau) = R^*_{21} (-\tau)$。
互相關不像卷積那樣滿足交換律,即
$$ R_{12} (\tau) \neq R_{21} (-\tau) $$
-
如果 R12(0) = 0,意味著如果 $ \int_{-\infty}^{\infty} x_1 (t) x_2^* (t) dt = 0$,則這兩個訊號被稱為正交。
對於功率訊號,如果 $ \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x^* (t)\,dt $,則這兩個訊號被稱為正交。
互相關函式對應於一個訊號的頻譜與另一個訊號頻譜的複共軛的乘積。即
$$ R_{12} (\tau) \leftarrow \rightarrow X_1(\omega) X_2^*(\omega)$$
這也被稱為相關定理。
帕塞瓦爾定理
帕塞瓦爾定理對於能量訊號指出,訊號的總能量可以透過訊號的頻譜獲得,如下所示
$ E = {1\over 2 \pi} \int_{-\infty}^{\infty} |X(\omega)|^2 d\omega $
注意:如果一個訊號具有能量 E,則該訊號的時間尺度版本 x(at) 具有能量 E/a。
訊號取樣定理
陳述:連續時間訊號可以表示為其樣本,並且當取樣頻率 fs 大於或等於訊息訊號最高頻率分量的兩倍時,可以恢復回原始訊號。即
$$ f_s \geq 2 f_m. $$
證明:考慮一個連續時間訊號 x(t)。x(t) 的頻譜限制在 fm Hz 內,即 x(t) 的頻譜對於 |ω|>ωm 為零。
輸入訊號 x(t) 的取樣可以透過將 x(t) 與週期為 Ts 的脈衝序列 δ(t) 相乘來獲得。乘法器的輸出是稱為取樣訊號的離散訊號,在以下圖中用 y(t) 表示

在這裡,您可以觀察到取樣訊號採用脈衝的週期。取樣過程可以透過以下數學表示式解釋
$ \text{取樣訊號}\, y(t) = x(t) . \delta(t) \,\,...\,...(1) $
$\delta$(t) 的三角傅立葉級數表示如下
$ \delta(t)= a_0 + \Sigma_{n=1}^{\infty}(a_n \cos n\omega_s t + b_n \sin n\omega_s t )\,\,...\,...(2) $
其中 $ a_0 = {1\over T_s} \int_{-T \over 2}^{ T \over 2} \delta (t)dt = {1\over T_s} \delta(0) = {1\over T_s} $
$ a_n = {2 \over T_s} \int_{-T \over 2}^{T \over 2} \delta (t) \cos n\omega_s\, dt = { 2 \over T_2} \delta (0) \cos n \omega_s 0 = {2 \over T}$
$b_n = {2 \over T_s} \int_{-T \over 2}^{T \over 2} \delta(t) \sin n\omega_s t\, dt = {2 \over T_s} \delta(0) \sin n\omega_s 0 = 0 $
將上述值代入公式 2。
$\therefore\, \delta(t)= {1 \over T_s} + \Sigma_{n=1}^{\infty} ( { 2 \over T_s} \cos n\omega_s t+0)$
將 δ(t) 代入公式 1。
$\to y(t) = x(t) . \delta(t) $
$ = x(t) [{1 \over T_s} + \Sigma_{n=1}^{\infty}({2 \over T_s} \cos n\omega_s t) ] $
$ = {1 \over T_s} [x(t) + 2 \Sigma_{n=1}^{\infty} (\cos n\omega_s t) x(t) ] $
$ y(t) = {1 \over T_s} [x(t) + 2\cos \omega_s t.x(t) + 2 \cos 2\omega_st.x(t) + 2 \cos 3\omega_s t.x(t) \,...\, ...\,] $
對兩邊進行傅立葉變換。
$Y(\omega) = {1 \over T_s} [X(\omega)+X(\omega-\omega_s )+X(\omega+\omega_s )+X(\omega-2\omega_s )+X(\omega+2\omega_s )+ \,...] $
$\therefore\,\, Y(\omega) = {1\over T_s} \Sigma_{n=-\infty}^{\infty} X(\omega - n\omega_s )\quad\quad where \,\,n= 0,\pm1,\pm2,... $
為了重建 x(t),必須從取樣訊號頻譜 Y(ω) 中恢復輸入訊號頻譜 X(ω),當 Y(ω) 的週期之間沒有重疊時,這是可能的。
不同條件下采樣頻率頻譜的可能性由以下圖給出
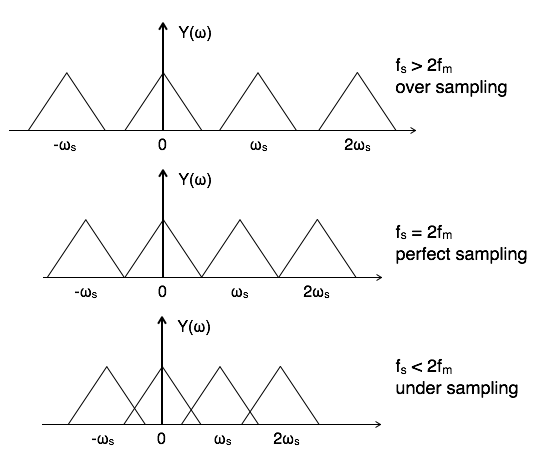
混疊效應
欠取樣情況下重疊區域表示混疊效應,可以透過以下方法消除
考慮 fs >2fm
使用抗混疊濾波器。
訊號取樣技術
有三種類型的取樣技術
脈衝取樣。
自然取樣。
平頂取樣。
脈衝取樣
脈衝取樣可以透過將輸入訊號 x(t) 與週期為 'T' 的脈衝序列 $\Sigma_{n=-\infty}^{\infty}\delta(t-nT)$ 相乘來執行。這裡,脈衝的幅度隨著輸入訊號 x(t) 的幅度而變化。取樣器的輸出由下式給出
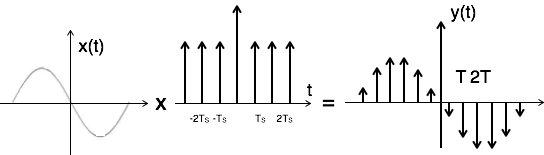
$y(t) = x(t) ×$ 脈衝序列
$= x(t) × \Sigma_{n=-\infty}^{\infty} \delta(t-nT)$
$ y(t) = y_{\delta} (t) = \Sigma_{n=-\infty}^{\infty}x(nt) \delta(t-nT)\,...\,... 1 $
為了獲得取樣訊號的頻譜,考慮對等式 1 的兩邊進行傅立葉變換
$Y(\omega) = {1 \over T} \Sigma_{n=-\infty}^{\infty} X(\omega - n \omega_s ) $
這被稱為理想取樣或脈衝取樣。在實踐中無法使用它,因為脈衝寬度不能為零,並且在實踐中不可能產生脈衝序列。
自然取樣
自然取樣類似於脈衝取樣,只是脈衝序列被週期為 T 的脈衝序列所取代。即,將輸入訊號 x(t) 乘以脈衝序列 $\Sigma_{n=-\infty}^{\infty} P(t-nT)$,如下所示

取樣器的輸出為
$y(t) = x(t) \times \text{脈衝序列}$
$= x(t) \times p(t) $
$= x(t) \times \Sigma_{n=-\infty}^{\infty} P(t-nT)\,...\,...(1) $
p(t) 的指數傅立葉級數表示可以寫成
$p(t) = \Sigma_{n=-\infty}^{\infty} F_n e^{j n\omega_s t}\,...\,...(2) $
$= \Sigma_{n=-\infty}^{\infty} F_n e^{j 2 \pi nf_s t} $
其中 $F_n= {1 \over T} \int_{-T \over 2}^{T \over 2} p(t) e^{-j n \omega_s t} dt$
$= {1 \over TP}(n \omega_s)$
將 Fn 的值代入公式 2
$ \therefore p(t) = \Sigma_{n=-\infty}^{\infty} {1 \over T} P(n \omega_s)e^{j n \omega_s t}$
$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)e^{j n \omega_s t}$
將 p(t) 代入公式 1
$y(t) = x(t) \times p(t)$
$= x(t) \times {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)\,e^{j n \omega_s t} $
$y(t) = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t} $
為了獲得取樣訊號的頻譜,考慮對兩邊進行傅立葉變換。
$F.T\, [ y(t)] = F.T [{1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t}]$
$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,F.T\,[ x(t)\, e^{j n \omega_s t} ] $
根據頻率移位特性
$F.T\,[ x(t)\, e^{j n \omega_s t} ] = X[\omega-n\omega_s] $
$ \therefore\, Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,X[\omega-n\omega_s] $
平頂取樣
在傳輸過程中,會在傳輸脈衝的頂部引入噪聲,如果脈衝呈平頂狀,則可以很容易地去除噪聲。這裡,樣本的頂部是平坦的,即它們具有恆定的幅度。因此,它被稱為平頂取樣或實際取樣。平頂取樣利用取樣保持電路。

從理論上講,取樣訊號可以透過矩形脈衝 p(t) 與理想取樣訊號(例如 yδ(t))的卷積來獲得,如圖所示
即 $ y(t) = p(t) \times y_\delta (t)\, ... \, ...(1) $
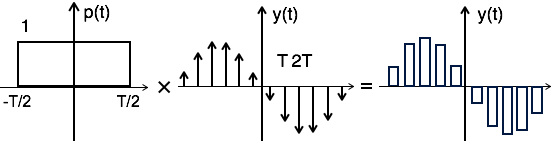
為了獲得取樣頻譜,考慮對等式 1 的兩邊進行傅立葉變換
$Y[\omega] = F.T\,[P(t) \times y_\delta (t)] $
根據卷積特性,
$Y[\omega] = P(\omega)\, Y_\delta (\omega)$
這裡 $P(\omega) = T Sa({\omega T \over 2}) = 2 \sin \omega T/ \omega$
奈奎斯特率
它是將訊號轉換為樣本並能夠在不失真地恢復回原始訊號的最低取樣率。
奈奎斯特率 fN = 2fm hz
奈奎斯特間隔 = ${1 \over fN}$ = $ {1 \over 2fm}$ 秒。
帶通訊號的取樣
對於帶通訊號,帶通訊號 X[ω] 的頻譜對於頻率範圍外的頻率 f1 ≤ f ≤ f2 為 0。頻率 f1 始終大於零。此外,當 fs > 2f2 時,沒有混疊效應。但它有兩個缺點
取樣率與 f2 成正比。這在實踐中有一定的侷限性。
取樣訊號頻譜存在頻譜間隙。
為了克服這一點,帶通定理指出,當取樣頻率 fs < 2f2 時,輸入訊號 x(t) 可以轉換為其樣本並可以恢復回原始訊號,而不會產生失真。
此外,
$$ f_s = {1 \over T} = {2f_2 \over m} $$
其中 m 是小於 ${f_2 \over B}$ 的最大整數
且 B 是訊號的頻寬。如果 f2=KB,則
$$ f_s = {1 \over T} = {2KB \over m} $$
對於頻寬為 2fm 的帶通訊號和最小取樣率 fs= 2 B = 4fm,
取樣訊號的頻譜由 $Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty}\,X[ \omega - 2nB]$ 給出
拉普拉斯變換 (LT)
復傅立葉變換也稱為雙邊拉普拉斯變換。它用於求解微分方程。考慮一個由形式為 x(t) = Gest 的復指數訊號激勵的 LTI 系統。
其中 s = 任何複數 = $\sigma + j\omega$,
σ = s 的實部,以及
ω = s 的虛部
LTI 的響應可以透過輸入與其脈衝響應的卷積來獲得,即
$ y(t) = x(t) \times h(t) = \int_{-\infty}^{\infty}\, h (\tau)\, x (t-\tau)d\tau $
$= \int_{-\infty}^{\infty}\, h (\tau)\, Ge^{s(t-\tau)}d\tau $
$= Ge^{st}. \int_{-\infty}^{\infty}\, h (\tau)\, e^{(-s \tau)}d\tau $
$ y(t) = Ge^{st}.H(S) = x(t).H(S)$
其中 H(S) = $h(\tau)$ 的拉普拉斯變換 = $\int_{-\infty}^{\infty} h (\tau) e^{-s\tau} d\tau $
類似地,$x(t)$ 的拉普拉斯變換 = X(S) = $\int_{-\infty}^{\infty} x(t) e^{-st} dt\,...\,...(1)$
拉普拉斯變換和傅立葉變換之間的關係
$x(t)$ 的拉普拉斯變換 = X(S) =$\int_{-\infty}^{\infty} x(t) e^{-st} dt$
將 s= σ + jω 代入上述公式。
$→ X(\sigma+j\omega) =\int_{-\infty}^{\infty}\,x (t) e^{-(\sigma+j\omega)t} dt$
$ = \int_{-\infty}^{\infty} [ x (t) e^{-\sigma t}] e^{-j\omega t} dt $
$\therefore X(S) = F.T [x (t) e^{-\sigma t}]\,...\,...(2)$
$X(S) = X(\omega) \quad\quad for\,\, s= j\omega$
拉普拉斯逆變換
您知道 $X(S) = F.T [x (t) e^{-\sigma t}]$
$\to x (t) e^{-\sigma t} = F.T^{-1} [X(S)] = F.T^{-1} [X(\sigma+j\omega)]$
$= {1\over 2}\pi \int_{-\infty}^{\infty} X(\sigma+j\omega) e^{j\omega t} d\omega$
$ x (t) = e^{\sigma t} {1 \over 2\pi} \int_{-\infty}^{\infty} X(\sigma+j\omega) e^{j\omega t} d\omega $
$= {1 \over 2\pi} \int_{-\infty}^{\infty} X(\sigma+j\omega) e^{(\sigma+j\omega)t} d\omega \,...\,...(3)$
這裡,$\sigma+j\omega = s$
$jdω = ds → dω = ds/j$
$ \therefore x (t) = {1 \over 2\pi j} \int_{-\infty}^{\infty} X(s) e^{st} ds\,...\,...(4) $
公式 1 和 4 分別表示訊號 x(t) 的拉普拉斯變換和拉普拉斯逆變換。
拉普拉斯變換存在的條件
狄利克雷條件用於定義拉普拉斯變換的存在性。即
函式 f(t) 具有有限個最大值和最小值。
在給定的時間間隔內,訊號 f(t) 必須具有有限個不連續點。
它必須在給定的時間間隔內絕對可積。即
$ \int_{-\infty}^{\infty} |\,f(t)|\, dt \lt \infty $
初始值定理和終值定理
如果已知未知函式 x(t) 的拉普拉斯變換,則可以確定該未知訊號的初始值和終值,即 x(t) 在 t=0+ 和 t=∞ 時的值。
初始值定理
敘述:如果 x(t) 及其一階導數是拉普拉斯可變換的,則 x(t) 的初始值由下式給出
$$ x(0^+) = \lim_{s \to \infty} SX(S) $$
終值定理
敘述:如果 x(t) 及其一階導數是拉普拉斯可變換的,則 x(t) 的終值由下式給出
$$ x(\infty) = \lim_{s \to \infty} SX(S) $$
拉普拉斯變換性質
拉普拉斯變換的性質如下
線性性質
如果 $\,x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
& $\, y(t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} Y(s)$
則線性性質指出
$a x (t) + b y (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} a X(s) + b Y(s)$
時移性質
如果 $\,x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
則時間推移性質表明
$x (t-t_0) \stackrel{\mathrm{L.T}}{\longleftrightarrow} e^{-st_0 } X(s)$
頻移性質
如果 $\, x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
則頻移性質指出
$e^{s_0 t} . x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s-s_0)$
時間反轉性質
如果 $\,x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
則時間反轉性質表明
$x (-t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(-s)$
時間縮放性質
如果 $\,x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
則時間尺度變換性質表明
$x (at) \stackrel{\mathrm{L.T}}{\longleftrightarrow} {1\over |a|} X({s\over a})$
微分和積分性質
如果 $\, x (t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
則微分性質表明
$ {dx (t) \over dt} \stackrel{\mathrm{L.T}}{\longleftrightarrow} s. X(s) - s. X(0) $
${d^n x (t) \over dt^n} \stackrel{\mathrm{L.T}}{\longleftrightarrow} (s)^n . X(s)$
積分性質表明
$\int x (t) dt \stackrel{\mathrm{L.T}}{\longleftrightarrow} {1 \over s} X(s)$
$\iiint \,...\, \int x (t) dt \stackrel{\mathrm{L.T}}{\longleftrightarrow} {1 \over s^n} X(s)$
乘法和卷積性質
如果 $\,x(t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s)$
且 $ y(t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} Y(s)$
則乘法性質指出
$x(t). y(t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} {1 \over 2 \pi j} X(s)*Y(s)$
卷積性質表明
$x(t) * y(t) \stackrel{\mathrm{L.T}}{\longleftrightarrow} X(s).Y(s)$
收斂域 (ROC)
拉普拉斯變換收斂的 σ 的取值範圍稱為收斂域。
拉普拉斯變換收斂域的性質
收斂域包含 s 平面上平行於 jω 軸的帶狀區域。
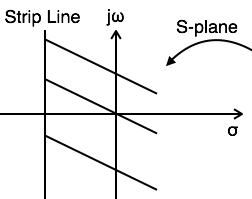
如果 x(t) 是絕對可積的且是有限持續時間的,則收斂域是整個 s 平面。
如果 x(t) 是右邊的序列,則收斂域:Re{s} > σo。
如果 x(t) 是左邊的序列,則收斂域:Re{s} < σo。
如果 x(t) 是雙邊序列,則收斂域是兩個區域的組合。
可以透過以下示例來解釋收斂域
示例 1:求 $x(t) = e-^{at}u(t)$ 的拉普拉斯變換和收斂域
$L.T[x(t)] = L.T[e-^{at}u(t)] = {1 \over S+a}$
$ Re{} \gt -a $
$ ROC:Re{s} \gt >-a$
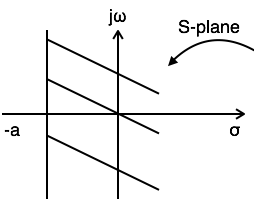
示例 2:求 $x(t) = e^{at}u(-t)$ 的拉普拉斯變換和收斂域
$ L.T[x(t)] = L.T[e^{at}u(t)] = {1 \over S-a} $
$ Re{s} < a $
$ ROC: Re{s} < a $
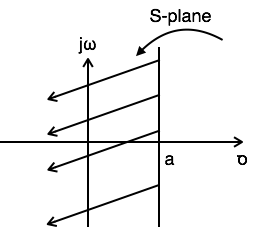
示例 3:求 $x(t) = e^{-at}u(t)+e^{at}u(-t)$ 的拉普拉斯變換和收斂域
$L.T[x(t)] = L.T[e^{-at}u(t)+e^{at}u(-t)] = {1 \over S+a} + {1 \over S-a}$
對於 ${1 \over S+a} Re\{s\} \gt -a $
對於 ${1 \over S-a} Re\{s\} \lt a $
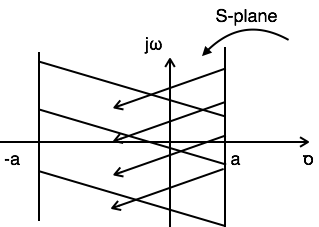
參考上圖,組合區域位於 –a 到 a 之間。因此,
$ ROC: -a < Re{s} < a $
因果性和穩定性
為了使系統具有因果性,其傳遞函式的所有極點必須位於 s 平面的右半部分。
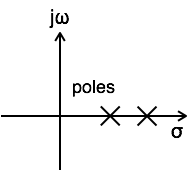
當傳遞函式的所有極點都位於 s 平面的左半部分時,系統被稱為穩定。
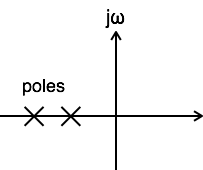
當傳遞函式的至少一個極點移到 s 平面的右半部分時,系統被稱為不穩定。
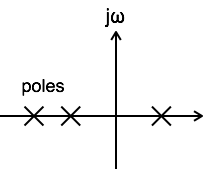
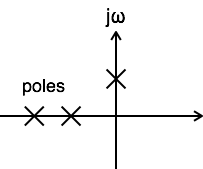
當傳遞函式的至少一個極點位於 s 平面的 jω 軸上時,系統被稱為臨界穩定。
基本函式的 ROC
| f(t) | F(s) | ROC |
|---|---|---|
| $u(t)$ | $${1\over s}$$ | ROC: Re{s} > 0 |
| $ t\, u(t) $ | $${1\over s^2} $$ | ROC:Re{s} > 0 |
| $ t^n\, u(t) $ | $$ {n! \over s^{n+1}} $$ | ROC:Re{s} > 0 |
| $ e^{at}\, u(t) $ | $$ {1\over s-a} $$ | ROC:Re{s} > a |
| $ e^{-at}\, u(t) $ | $$ {1\over s+a} $$ | ROC:Re{s} > -a |
| $ e^{at}\, u(t) $ | $$ - {1\over s-a} $$ | ROC:Re{s} < a |
| $ e^{-at}\, u(-t) $ | $$ - {1\over s+a} $$ | ROC:Re{s} < -a |
| $ t\, e^{at}\, u(t) $ | $$ {1 \over (s-a)^2} $$ | ROC:Re{s} > a |
| $ t^{n} e^{at}\, u(t) $ | $$ {n! \over (s-a)^{n+1}} $$ | ROC:Re{s} > a |
| $ t\, e^{-at}\, u(t) $ | $$ {1 \over (s+a)^2} $$ | ROC:Re{s} > -a |
| $ t^n\, e^{-at}\, u(t) $ | $${n! \over (s+a)^{n+1}} $$ | ROC:Re{s} > -a |
| $ t\, e^{at}\, u(-t) $ | $$ - {1 \over (s-a)^2} $$ | ROC:Re{s} < a |
| $ t^n\, e^{at}\, u(-t) $ | $$ - {n! \over (s-a)^{n+1}} $$ | ROC:Re{s} < a |
| $ t\, e^{-at}\,u(-t) $ | $$ - {1 \over (s+a)^2} $$ | ROC:Re{s} < -a |
| $ t^n\, e^{-at}\, u(-t) $ | $$ - {n! \over (s+a)^{n+1}} $$ | ROC:Re{s} < -a |
| $ e^{-at} \cos \, bt $ | $$ {s+a \over (s+a)^2 + b^2 } $$ | |
| $ e^{-at} \sin\, bt $ | $$ {b \over (s+a)^2 + b^2 } $$ |
Z 變換 (ZT)
可以使用 z 變換對連續時間 LTI 系統進行分析。它是一種強大的數學工具,可以將微分方程轉換為代數方程。
離散時間訊號 x(n) 的雙邊(雙側)z 變換表示為
$Z.T[x(n)] = X(Z) = \Sigma_{n = -\infty}^{\infty} x(n)z^{-n} $
離散時間訊號 x(n) 的單邊(單側)z 變換表示為
$Z.T[x(n)] = X(Z) = \Sigma_{n = 0}^{\infty} x(n)z^{-n} $
對於某些離散時間傅立葉變換 (DTFT) 不存在的訊號,z 變換可能存在。
Z 變換和反 Z 變換的概念
離散時間訊號 x(n) 的 z 變換可以用 X(Z) 表示,其定義為
$X(Z) = \Sigma_{n=- \infty }^ {\infty} x(n)z^{-n} \,...\,...\,(1)$
如果 $Z = re^{j\omega}$,則方程 1 變為
$X(re^{j\omega}) = \Sigma_{n=- \infty}^{\infty} x(n)[re^{j \omega} ]^{-n}$
$= \Sigma_{n=- \infty}^{\infty} x(n)[r^{-n} ] e^{-j \omega n}$
$X(re^{j \omega} ) = X(Z) = F.T[x(n)r^{-n}] \,...\,...\,(2) $
上述方程表示傅立葉變換和 z 變換之間的關係。
$ X(Z) |_{z=e^{j \omega}} = F.T [x(n)]. $
反 Z 變換
$X(re^{j \omega}) = F.T[x(n)r^{-n}] $
$x(n)r^{-n} = F.T^{-1}[X(re^{j \omega}]$
$x(n) = r^n\,F.T^{-1}[X(re^{j \omega} )]$
$= r^n {1 \over 2\pi} \int X(re{^j \omega} )e^{j \omega n} d \omega $
$= {1 \over 2\pi} \int X(re{^j \omega} )[re^{j \omega} ]^n d \omega \,...\,...\,(3)$
將 $re^{j \omega} = z$ 代入。
$dz = jre^{j \omega} d \omega = jz d \omega$
$d \omega = {1 \over j }z^{-1}dz$
代入方程 3。
$ 3\, \to \, x(n) = {1 \over 2\pi} \int\, X(z)z^n {1 \over j } z^{-1} dz = {1 \over 2\pi j} \int \,X(z) z^{n-1} dz $
$$X(Z) = \sum_{n=- \infty }^{\infty} \,x(n)z^{-n}$$ $$x(n) = {1 \over 2\pi j} \int\, X(z) z^{n-1} dz$$
Z 變換性質
Z 變換具有以下性質
線性性質
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
則線性性質指出
$a\, x (n) + b\, y (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} a\, X(Z) + b\, Y(Z)$
時移性質
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
則時移性質指出
$x (n-m) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} z^{-m} X(Z)$
指數序列相乘性質
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
則指數序列相乘性質表明
$a^n\, . x(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z/a)$
時間反轉性質
如果 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
則時間反轉性質表明
$x (-n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(1/Z)$
Z 域微分或 n 相乘性質
如果 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
則 n 相乘或 Z 域微分性質表明
$ n^k x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} [-1]^k z^k{d^k X(Z) \over dZ^K} $
卷積性質
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
則卷積性質表明
$x(n) * y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z)$
相關性性質
如果 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
且 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
則相關性性質表明
$x(n) \otimes y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z^{-1})$
初始值和終值定理
z 變換的初始值和終值定理針對因果訊號定義。
初始值定理
對於因果訊號 x(n),初始值定理表明
$ x (0) = \lim_{z \to \infty }X(z) $
這用於在不進行反 z 變換的情況下找到訊號的初始值
終值定理
對於因果訊號 x(n),終值定理表明
$ x ( \infty ) = \lim_{z \to 1} [z-1] X(z) $
這用於在不進行反 z 變換的情況下找到訊號的終值。
Z 變換的收斂域 (ROC)
z 變換收斂的 z 取值範圍稱為 z 變換的收斂域。
Z 變換收斂域的性質
z 變換的收斂域在 z 平面上用圓表示。
收斂域不包含任何極點。
如果 x(n) 是有限持續時間的因果序列或右邊的序列,則收斂域是整個 z 平面,除了 z = 0。
如果 x(n) 是有限持續時間的反因果序列或左邊的序列,則收斂域是整個 z 平面,除了 z = ∞。
如果 x(n) 是無限持續時間的因果序列,則收斂域是半徑為 a 的圓的外部,即 |z| > a。
如果 x(n) 是無限持續時間的反因果序列,則收斂域是半徑為 a 的圓的內部,即 |z| < a。
如果 x(n) 是有限持續時間的雙邊序列,則收斂域是整個 z 平面,除了 z = 0 和 z = ∞。
以下示例可以解釋 ROC 的概念
示例 1:求 $a^n u[n] + a^{-}nu[-n-1]$ 的 z 變換和 ROC
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z \over Z-a} + {Z \over Z {-1 \over a}}$
$$ ROC: |z| \gt a \quad\quad ROC: |z| \lt {1 \over a} $$
ROC 的圖有兩個條件,a > 1 和 a < 1,因為您不知道 a 的值。

在這種情況下,沒有組合 ROC。

這裡,ROC 的組合是 $a \lt |z| \lt {1 \over a}$
因此,對於此問題,當 a < 1 時,z 變換是可能的。
因果性和穩定性
離散時間 LTI 系統的因果性條件如下
當以下條件滿足時,離散時間 LTI 系統是因果的
ROC 在最外層極點的外部。
在傳遞函式 H[Z] 中,分子的階數不能大於分母的階數。
離散時間 LTI 系統的穩定性條件
當以下條件滿足時,離散時間 LTI 系統是穩定的
其系統函式 H[Z] 包含單位圓 |z|=1。
傳遞函式的所有極點都位於單位圓 |z|=1 的內部。
基本訊號的 Z 變換
| x(t) | X[Z] |
|---|---|
| $\delta$ | 1 |
| $u(n)$ | ${Z\over Z-1}$ |
| $u(-n-1)$ | $ -{Z\over Z-1}$ |
| $\delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z \over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z \over Z-a}$ |
| $n\,a^n u[n]$ | ${aZ \over |Z-a|^2}$ |
| $n\,a^n u[-n-1] $ | $- {aZ \over |Z-a|^2}$ |
| $a^n \cos \omega n u[n] $ | ${Z^2-aZ \cos \omega \over Z^2-2aZ \cos \omega +a^2}$ |
| $a^n \sin \omega n u[n] $ | $ {aZ \sin \omega \over Z^2 -2aZ \cos \omega +a^2 } $ |
