
- 訊號與系統教程
- 訊號與系統首頁
- 訊號與系統概述
- 訊號基本型別
- 訊號分類
- 訊號基本運算
- 系統分類
- 訊號分析
- 傅立葉級數
- 傅立葉級數性質
- 傅立葉級數型別
- 傅立葉變換
- 傅立葉變換性質
- 無失真傳輸
- 希爾伯特變換
- 卷積與相關
- 訊號取樣定理
- 訊號取樣技術
- 拉普拉斯變換
- 拉普拉斯變換性質
- 收斂域
- Z變換 (ZT)
- Z變換性質
- 訊號與系統資源
- 訊號與系統 - 資源
- 訊號與系統 - 討論
收斂域 (ROC)
使拉普拉斯變換收斂的σ的取值範圍稱為收斂域。
拉普拉斯變換收斂域的性質
ROC在s平面包含平行於jω軸的條帶。
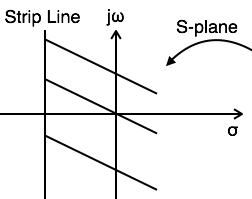
如果x(t)是絕對可積的且是有限持續時間的,則ROC是整個s平面。
如果x(t)是右側序列,則ROC:Re{s} > σo。
如果x(t)是左側序列,則ROC:Re{s} < σo。
如果x(t)是雙側序列,則ROC是兩個區域的組合。
可以使用以下示例來解釋ROC
示例1:求x(t) = e-atu(t)的拉普拉斯變換和ROC
L.T[x(t)] = L.T[e-atu(t)] = 1/(s+a)
Re{s} > -a
ROC: Re{s} > -a
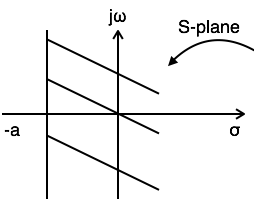
示例2:求x(t) = eatu(-t)的拉普拉斯變換和ROC
L.T[x(t)] = L.T[eatu(-t)] = 1/(s-a)
Re{s} < a
ROC: Re{s} < a
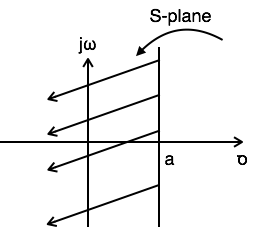
示例3:求x(t) = e-atu(t) + eatu(-t)的拉普拉斯變換和ROC
L.T[x(t)] = L.T[e-atu(t) + eatu(-t)] = 1/(s+a) + 1/(s-a)
對於1/(s+a),Re{s} > -a
對於1/(s-a),Re{s} < a
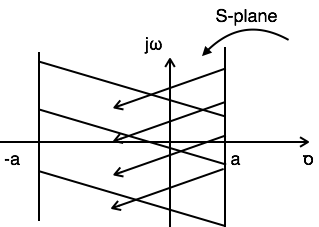
參考上圖,組合區域位於-a到a之間。因此,
ROC: -a < Re{s} < a
因果性和穩定性
為了使系統具有因果性,其傳遞函式的所有極點必須位於s平面的右半平面。
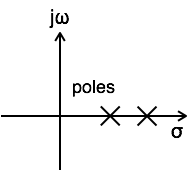
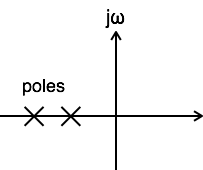
當其傳遞函式的所有極點都位於s平面的左半平面時,系統被稱為穩定。
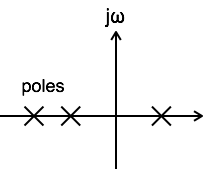
當其傳遞函式至少有一個極點位於s平面的右半平面時,系統被稱為不穩定。
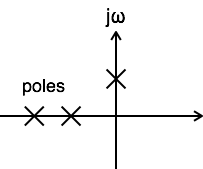
當其傳遞函式至少有一個極點位於s平面的jω軸上時,系統被稱為臨界穩定。
基本函式的ROC
| f(t) | F(s) | ROC |
|---|---|---|
| u(t) | 1/s | ROC: Re{s} > 0 |
| t u(t) | 1/s² | ROC: Re{s} > 0 |
| tn u(t) | n!/sn+1 | ROC: Re{s} > 0 |
| eat u(t) | 1/(s-a) | ROC: Re{s} > a |
| e-at u(t) | 1/(s+a) | ROC: Re{s} > -a |
| eat u(t) | -1/(s-a) | ROC: Re{s} < a |
| e-at u(-t) | -1/(s+a) | ROC: Re{s} < -a |
| t eat u(t) | 1/(s-a)² | ROC: Re{s} > a |
| tn eat u(t) | n!/(s-a)n+1 | ROC: Re{s} > a |
| t e-at u(t) | 1/(s+a)² | ROC: Re{s} > -a |
| tn e-at u(t) | n!/(s+a)n+1 | ROC: Re{s} > -a |
| t eat u(-t) | -1/(s-a)² | ROC: Re{s} < a |
| tn eat u(-t) | -n!/(s-a)n+1 | ROC: Re{s} < a |
| t e-at u(-t) | -1/(s+a)² | ROC: Re{s} < -a |
| tn e-at u(-t) | -n!/(s+a)n+1 | ROC: Re{s} < -a |
| e-atcos(bt) | (s+a)/((s+a)² + b²) | |
| e-atsin(bt) | b/((s+a)² + b²) |
廣告
