訊號基本運算

---

---

一般來說，有兩個變數引數

1. 幅度
2. 時間

以下運算可以對幅度進行

幅度縮放

C x(t) 是 x(t) 的幅度縮放版本，其幅度按因子 C 縮放。

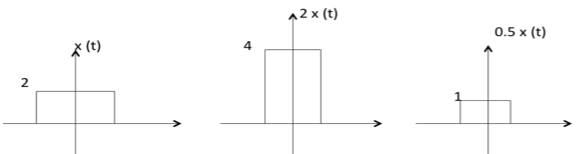
加法

兩個訊號的加法就是它們對應幅度的加法。這可以用以下示例最好地解釋

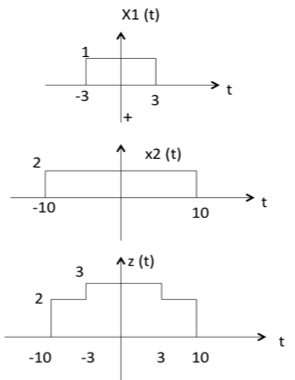
從上圖可以看出，

-10 < t < -3 時，z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2

-3 < t < 3 時，z(t) 的幅度 = x1(t) + x2(t) = 1 + 2 = 3

3 < t < 10 時，z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2

減法

兩個訊號的減法就是它們對應幅度的減法。這可以用以下示例最好地解釋

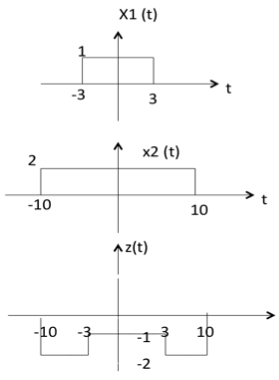
從上圖可以看出，

-10 < t < -3 時，z(t) 的幅度 = x1(t) - x2(t) = 0 - 2 = -2

-3 < t < 3 時，z(t) 的幅度 = x1(t) - x2(t) = 1 - 2 = -1

3 < t < 10 時，z(t) 的幅度 = x1(t) + x2(t) = 0 - 2 = -2

乘法

兩個訊號的乘法就是它們對應幅度的乘法。這可以用以下示例最好地解釋

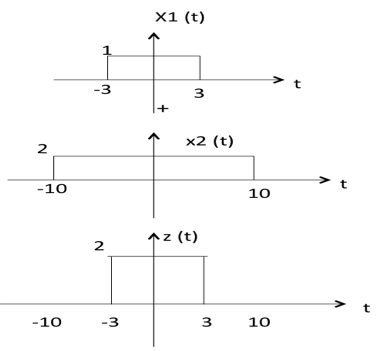
從上圖可以看出，

-10 < t < -3 時，z(t) 的幅度 = x1(t) ×x2(t) = 0 ×2 = 0

-3 < t < 3 時，z(t) 的幅度 = x1(t) ×x2(t) = 1 ×2 = 2

3 < t < 10 時，z(t) 的幅度 = x1(t) × x2(t) = 0 × 2 = 0

以下運算可以對時間進行

時間移位

x(t $\pm$ t₀) 是訊號 x(t) 的時間移位版本。

x (t + t₀) $\to$ 負移位

x (t - t₀) $\to$ 正移位

時間縮放

x(At) 是訊號 x(t) 的時間縮放版本，其中 A 始終為正。

|A| > 1 $\to$ 訊號壓縮

|A| < 1 $\to$ 訊號擴充套件

注意：u(at) = u(t) 時間縮放不適用於單位階躍函式。

時間反轉

x(-t) 是訊號 x(t) 的時間反轉。